Introduction
CTR预估(click-through-rate prediction)是广告行业比较常见的问题,根据用户的历史行为来判断用户对广告点击的可能性。该问题的输入往往是数以万计的稀疏特征向量,在进行特征交叉后会维数会更高,比较常见的就是采用对率回归模型加一些正则化,因为对率回归模型计算开销小且容易实现并行。之前facebook的一篇论文中先用树模型做分类之后再加一个对率回归模型,最后得出效果出奇的好,应该也是工业界比较常用的方法,同时树模型的选择或者说是再构造特征的特性也逐渐被大家所关注。另一种比较有效的就是因子分解模型系列,包括FM和FFM,它们的主要思想就是构造交叉特征或者是二阶的特征来一起进行训练。
这篇文章中,作者主要提出了一种piece-wise的线性模型,并且给出了其在大规模数据上的训练算法,称之为LS-PLM(Large Scale Piecewise Linear Model),LS-PLM采用了分治的思想,先分成几个局部再用线性模型拟合,这两部都采用监督学习的方式,来优化总体的预测误差,总的来说有以下优势:
- 非线性,通过分区来达到拟合非线性函数的效果;
- scalability,这个应该叫可放缩性?大概是这个意思,与对率回归模型相似,都可以很好的处理复杂的样本与高伟的特征,并且做到了分布式并行;
- 稀疏性,对于在线学习系统,模型的稀疏性较为重要,所以采用了\(L_1\) 和\(L_{2,1}\) 正则化
Method
Formulation
记数据集为\(\{x_t,y_t\}|^n_{t=1}\) ,其中\(y_t\in\{0,1\}\) ,输入\(x_t\in\mathbb{R}^d\) 通常是高维稀疏数据,我们将模型描述为 \[ p(y=1|x)=g( \sum^m_{j=1}\sigma(u_j^Tx)\eta(w_j^Tx) ) \] 定义模型参数为 \[ \Theta=\{u_1,...,u_m,w_1,...,w_m\} \in\mathbb{R}^{d\times 2m} \] 其中\(\{u_1,...,u_m\}\) 是区域划分函数\(\sigma(\cdot)\) 的参数,\(\{w_1,...,w_m\}\) 是拟合函数\(\eta(\cdot)\) 的参数。给定样本\(x\) ,模型的预测\(p(y|x)\) 分为两部分:首先根据\(\sigma(u_j^Tx)\) 分割特征空间为\(m\) 部分,其中\(m\) 为给定的超参数,然后对于各部分计算\(\eta(w_j^Tx)\) 作为各部分的预测。函数\(g(\cdot)\) 确保了我们的模型满足概率函数的定义。
当我们将softmax函数作为分割函数\(\sigma(x)\) ,将sigmoid函数作为拟合函数\(\eta(x)\) 的时候,该模型为 \[ p(y=1|x)=\sum^m_{i=1} \frac{\exp(u_i^Tx)}{\sum^m_{j=1}\exp(u_j^Tx)} \cdot\frac{1}{1+\exp(-w_i^Tx)} \] 此时我们的混合模型可以看做一个FOE模型 \[ p(y=1|x)=\sum^m_{i=1}p(z=i|x)p(y|z=i,x) \] 在理想情况下,模型会有如下图的表现
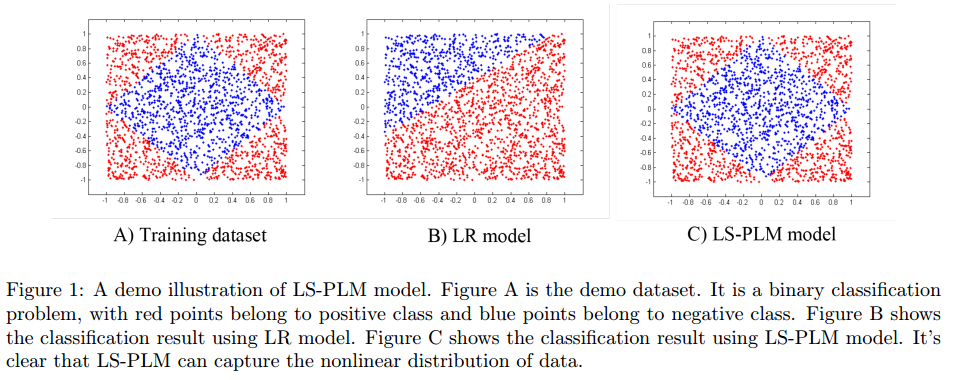
模型会很好的拟合数据的非线性关系。
LS-PLM模型可以表述为以下形式 \[ \arg min_\Theta f(\Theta)=loss(\Theta)+\lambda||\Theta||_{2,1}+\beta||\Theta||_1 \]
\[ loss(\Theta)=-\sum^n_{t=1}[ y_t\log(p(y_t=1|x_t,\Theta)+(1-y_t)log(p(y_t=0|x_t,\Theta)) ] \]
其中\(L_{2,1}\) 正则项为 \[ ||\Theta||{2,1}=\sum^d{i=1}\sqrt{\sum^{2m}{j=1}\Theta^2{ij}} \]
Optimization
作以下定义:\(\partial^+_{ij}f(\Theta)\) 为右导数 \[
\partial^+_{ij}f(\Theta)=\lim_{\alpha\rightarrow0}\frac{f(\Theta+\alpha
e_{ij})-f(\Theta)}{\alpha}
\] 其中\(e_{ij}\)
为单位偏差向量;\(f\) 在方向\(d\) 上的导数为\(f'(\Theta;d)\)
\[
f'(\Theta;d)=\lim_{\alpha\rightarrow0}\frac{f(\Theta+\alpha
d)-f(\Theta)}{\alpha}
\] 当\(f'(\Theta;d)<0\)
的时候\(d\) 是一个下降方向之一;\(sign(\cdot)\) 为取值是\(\{-1,0,1\}\) 的指示函数,则映射函数为 \[
\pi_{ij}(\Theta;\Omega)=\begin{cases}
\Theta_{ij}&, &sign(\Theta_{ij})=sign(\Omega_{ij}) \\
0&, & \text{otherwise} \end{cases}
\]
表示将\(\Theta\) 映射到象限\(\Omega\) 上。
因为目标函数非凸非连续,所以整体的梯度方向很难找到,所以可以选择非正的下降方向进行迭代 \[ d_{ij}=\begin{cases} s-\beta sign(\Theta_{ij}), &\Theta_{ij}\neq0\\ \max\{|s|-\beta, 0\}sign(s), & \Theta_{ij}=0,||\theta_{i\cdot}||_{2,1}\neq0\\ \frac{max{||v||_{2,1}-\lambda,0}}{||v||_{2,1}}v, &||\Theta_{i\cdot}||_{2,1}=0 \end{cases} \] 其中 \[ s=-\bigtriangledown loss(\Theta){ij}-\lambda\frac{\Theta{ij}}{||\Theta{i\cdot}||{2,1}} \] 和 \[ v=\max\{|-\bigtriangledown loss(\Theta){ij}|-\beta,0\}sign(-\bigtriangledown loss(\Theta){ij}) \] 因为目标函数非凸,所以不能保证Hessian矩阵半正定,所以有些情况无法用LBFGS来优化,所以灵活选择,当Hessian矩阵满足条件时选择二阶优化,不满足时选择一阶优化条件 $$
$$
\[ p_k=\begin{cases} \pi(H_kd^{(k)};d^{(k)}), & y^{(k)T}s^{(k)}>0\\ d^{(k)},&\text{otherwise} \end{cases} \]
迭代的公式为 \[ \Theta^{(k+1)}=\pi(\Theta^{(k)}+\alpha p_k;\xi^{(k)}) \] 其中 \[ \xi^{(k)}_{ij}=\begin{cases} sign(\Theta^{(k)}_{ij}), & \Theta^{(k)}_{ij}\neq 0\\ sign(d^{(k)}_{ij}),& \Theta^{(k)}_{ij}=0\\ \end{cases} \] 这步应该是对象限的限制,我没看太懂,好像是参考OWLQN method 。留个坑以后填。对目标函数的整体优化算法如下图所示

后面还有对并行训练方面的优化设计,我对这方面研究较少,就没有细细品读了。
Summary
整体来看这篇论文的idea挺简单有效的,而且是工程中出来的论文,对工程实现上的优化细节都很详细,这种小trick一般是很难在paper中学到的,可是在工程上确实是利器。文中有对所涉及优化问题的证明,能考虑到工程处理的优化细节并对其做出数学上的证明,十分精彩。同时,写作方面也特别出色,对相关模型涉及的引用,简洁明了,行文思路清晰,没有把简单的模型写得晦涩难懂,同时还满满trick的干货,算是一篇佳作吧,对作者路人转粉。
同时文末说LS-PLM在2012年就应用于阿里巴巴的ctr预估,果然大公司中处处是人才呀。