因为最近在公司搞一个实时性要求比较高的推荐,所以最近会看一些新闻推荐、实时推荐相关的论文,今天这篇是一篇比较老的增量学习+协同过滤的论文,想法很简单,就是在计算相似度时分类讨论,不同情况选择不同的增量方式,尽最大的可能性减少计算量。
传统的相似度计算方式为 \[ \text{sim}(u_x,u_y)=\frac {\sum^n_{h=1}(r_{u_x,i_h}-\overline{r_{u_x}})((r_{u_x,i_h}-\overline{r_{u_y}})} {\sqrt{\sum^{n'}_{h=1}(r_{u_x,i_h}-\overline{r_{u_x}}\sum^{n'}_{h=1}(r_{u_y,i_h}-\overline{r_{u_y}}))}} \]
\[ A=\frac{B}{\sqrt{C}\sqrt{D}} \]
增量的计算方式为 \[ A=\frac{B'}{\sqrt{C'}\sqrt{D'}}=\frac{B+e}{\sqrt{C+f}\sqrt{D+g}} \] 然后作者就给出了不同情况下的更新方式
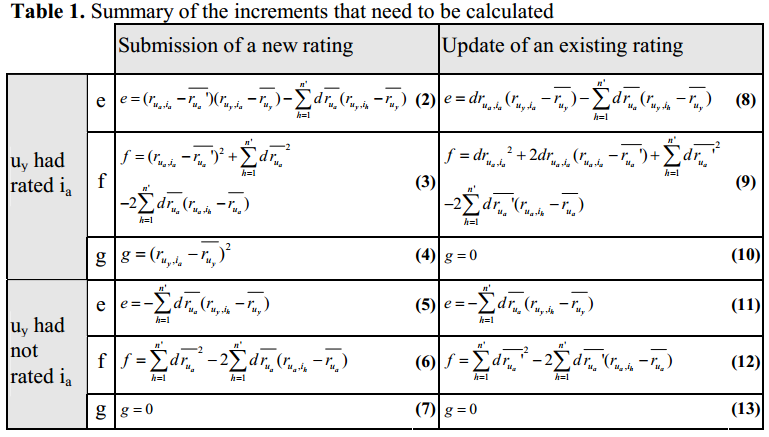
以及经过简单的缓存与计算就可以快速迭代相似度
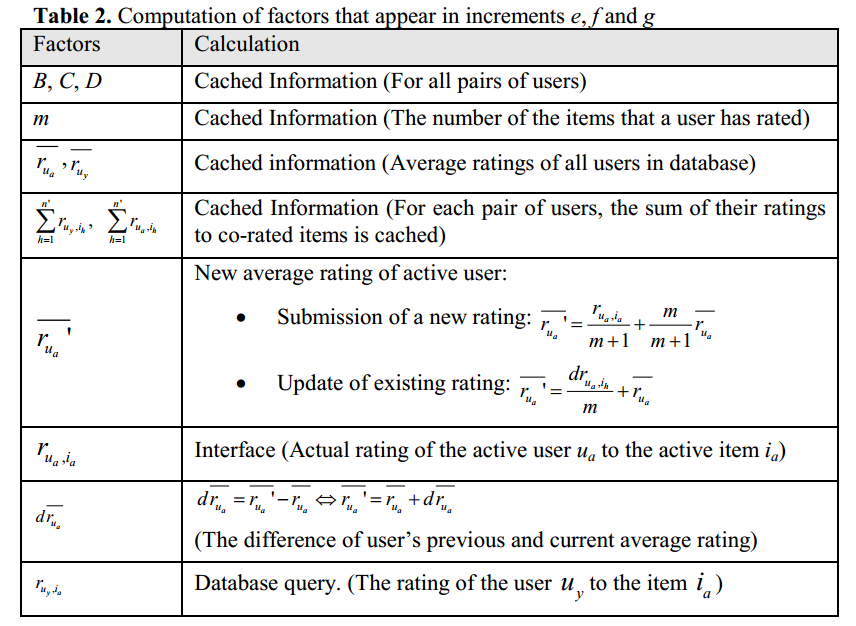
论文最后作者对各种情况的复杂度进行了分析,并进行了实验。
总的来说是一篇很基础的论文,我查了一下,2005年发表,引用100+,应该在当时也是种很实用的方法吧。