这篇文章是刚中的icml2020,刚好正中最近工作的痛点之一,拿出来写写。这篇文章主要是在写估计CATE时候,所面临的模型选择问题,与之前的思路不同的是,这篇文章通过CATE estimator的表现的排序来选择模型,获得更高准确度、更稳定的模型。
在模型评估和选择上,因果模型相较于一般的机器学习模型会受到更多的挑战,因为无法直接观测到ground truth,所以无法采用诸如mse之类的指标,所以常见的验证过程并无法直接指导CATE模型的模型选择和超参数调整,这就使得很难辨别出稳定的模型和合适的超参数。
之前有很多工作提出一些解决办法:
与之前工作不同的是,本文更关注于最优模型或超参数的选择,更关注于候选estimator的相对排序关系,与直接估计真正的表现相比更为简单。同时,分析模型评估的不确定性也十分重要,尤其在验证集可能很小的情况下。 符号定义如下,偷懒直接截图论文原文了:




在之前的研究中,对于一个CATE的predictor \(\hat{\tau}(\cdot)\)的评估,被定义为估计如下ground truth的精准程度,对于观测的验证集\({\cal{V}}=\{X_i,T_i,Y_i\}^n_{i=1}\): \[ \begin{aligned} {\cal{R}}_{true}(\hat{\tau})&={\Bbb{E}}[L(\tau(X),\hat{\tau}(X))] \\ &={\Bbb{E}}_X[(\tau(X),\hat{\tau}(X))^2] \end{aligned} \] 其中\({\cal{R}}_{true}\)是对\(\hat{\tau}(\cdot)\)的真实评估标准,这种方式比较理想,而真正的CATE是无法观测到的,因此这种准确的评估方式十分困难。同时,估计真正的指标值对于构建一个有效的模型选择并不是必须的,可以通过在某个特定目标下获得更好的评估指标来进行模型的选择和调整。因此我们选择了另一种不同于前人工作的方式来构建一个评估器\(\hat{\cal{R}}(\hat{\tau})\),满足以下条件: \[ \cal{R}_{true}(\hat{\tau})\leq\cal{R}_{true}(\hat{\tau}')\Rightarrow \hat{\cal{R}}_(\hat{\tau})\leq\hat{\cal{R}}(\hat{\tau}'),\forall\hat{\tau},\hat{\tau}'\in\cal{M} \] 其中\(\cal{M}=\{\hat{\tau}_1,\cdots,\hat{\tau}_{|\cal{M}|}\}\)是一些列侯选CATE estimator,一个满足上式关系的评估器能够选择出最优的模型。
为了达到以上目标,我们构建一个可行的估计器: \[ \hat{\cal{R}}(\hat{\tau})=\frac{1}{n}\sum^n_{i=1}(\tilde{\tau}(X_i,T_i,Y_i)-\hat{\tau}(X_i))^2 \] 其中\(\tilde{\tau}\)是一个plug-in \(\tau\),通过验证集计算得到,一般可以用double robust或者r-learner。那么接下来的问题就在于,如何选择构建一个好的plug-in \(\tau\)模型,来为侯选CATE模型在验证集上的表现排序。
假设我们拥有一个非偏的真实CATE的estimator,plug-in \(\tilde{\tau}\),即满足\({\Bbb{E}}[\tilde\tau(X,T,Y))|X]=\tau(X)\),则评估器\(\hat{\cal{R}}\)可以分解为 \[ \Bbb{E}[\hat{\cal{R}}(\hat{\tau})]={\cal{R}}_{true}(\hat{\tau})+\Bbb{E}[(\tau(X)-{\tilde{\tau}}(X,T,Y))^2] \] 上式中后一项与待评估的\(\hat{\tau}\)无关,所以会满足 \[ {\Bbb{E}[\hat{\cal{R}}(\hat{\tau}_1)]} - {\Bbb{E}[\hat{\cal{R}}(\hat{\tau}_2)]} = {\cal{R}}_{true}(\hat{\tau}_1) - {\cal{R}}_{true}(\hat{\tau}_2) \] 如果一个CATE的estimator在评估器\(\hat{\cal{R}}\)上拥有最小期望值,那这个模型就是所有候选模型中最优的模型。然而,往往我们验证集的数量并不会很多,这使得我们需要考虑评估器的不确定性。我们对其进行拆解

其中第二项\(\cal{W}\)式不确定性的关键,同时受到\(\tilde{\tau}\)的影响,所以我们尝试来降低\(\cal{W}\)的方差,以降低模型选择中的不确定性,通过各种公式推导,发现\(\cal{W}\)的方差的上界为

所以在构建一个plug-in \(\tau\)的时候,会倾向于构建一个更稳定的模型

接下来,文章里面提出了一种结合DR和CFR的模型,通过DR来满足无偏性,用CFR来最小化方差。
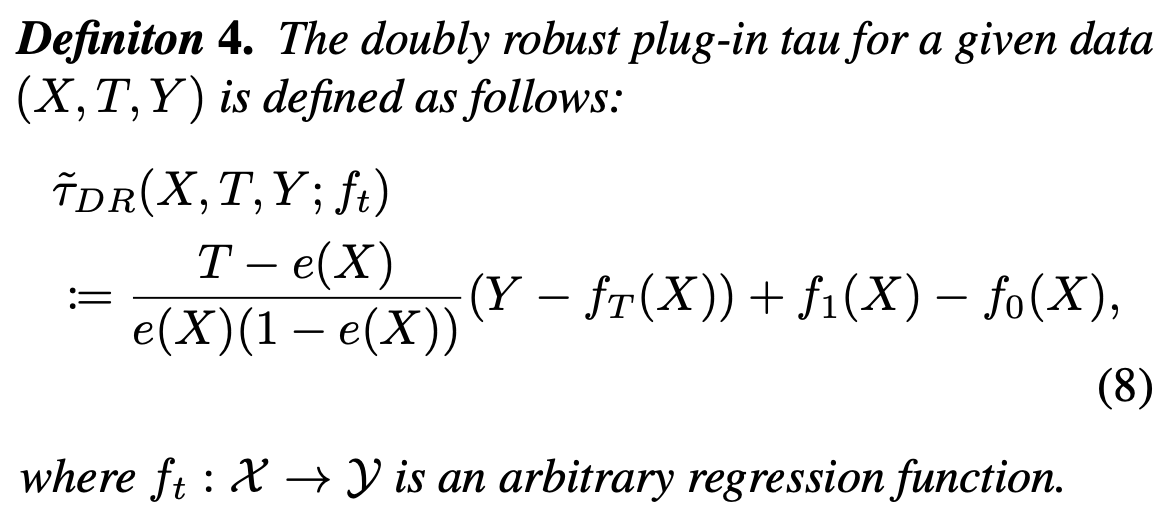
选择DR的框架,也是因为可以通过设计其中的regression function来达到某些目的,这里利用其来最小化我们有限样本上不确定性的上界,这些做法是无法通过IPW来实现的,同时需要注意的是,DR的框架使得我们只能用来评估而不能做预测。

通过拆解DR模型的方差,我们直接去优化regression function相关的部分,但是我们是无法直接优化上述目标,因为我们无法得到其中的\(m_0(x)\)和\(m_1(x)\),因为它们是反事实的结果,所以文中做了这个目标函数的上界

上式包含一个事实的loss和一个在表征空间上的ipm,因此它可以直接用观测到的样本估计出来,反事实的loss可以被事实的loss、treat和control的分布ipm的和bound住的。因此,我们可以用观测到的样本,以CFR的方式,优化这个DR方差条件期望的上界。

文中用上式作为公式11的近似,用NN来构建上述模型,总的算法如下

最终得到的plug-in \(\tilde{\tau}\)是一个无偏估计,同时最小化可控项方差的上界,可以得到精确且稳定的CATE预测模型的选择。
实验部分此处不细写了,大家感兴趣看论文吧。
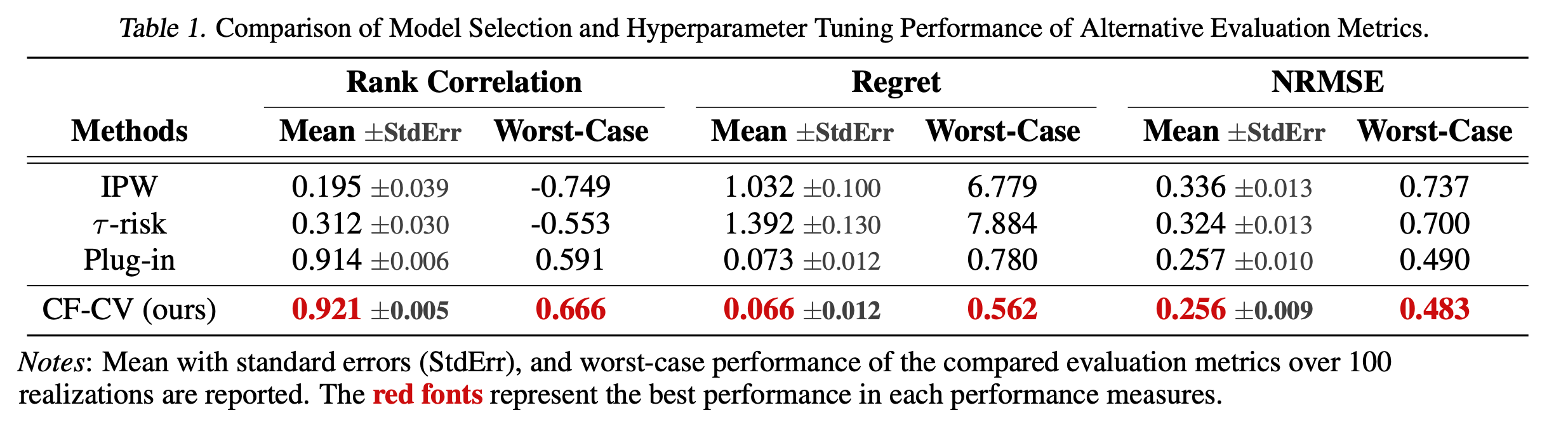
简单“人话”总结:用CFR+DR的方式,在validation set上构建一个CATE的预测,然后当成ground truth用于模型评估和选择。
吐槽:感觉最大问题在于,对plug-in \(\tau\)的unbiased的假设。。
reference
- Gutierrez, P. and Ge ́rardy, J.-Y. Causal inference and uplift
modelling: A review of the literature. In International Conference
on Predictive Applications and APIs, pp. 1– 13, 2017.
- Schuler, A., Baiocchi, M., Tibshirani, R., and Shah, N. A comparison
of methods for model selection when es- timating individual treatment
effects. arXiv preprint arXiv:1804.05146, 2018.
- Schuler, A., Baiocchi, M., Tibshirani, R., and Shah, N. A comparison of methods for model selection when es- timating individual treatment effects. arXiv preprint arXiv:1804.05146, 2018.