问题背景

现在在各大互联网平台上都存在着许多AB实验，服务每个用户所使用的机器学习模型、推荐系统参数、甚至UI界面等等，都由这些AB实验中配置的干预变量所决定的，通常我们会从众多干预中选择出表现最好的，进行全量，这种方式成为全局分配。

全局分配这种方式往往会是次优的，因为不同的干预对于每个用户或者说每个用户群体的效用，可能是不同的，全量某种干预方式很可能会给某个用户群体带来较差的用户体验，个性化干预的选择，可以带来更好的用户体验以及更多的商业增长。

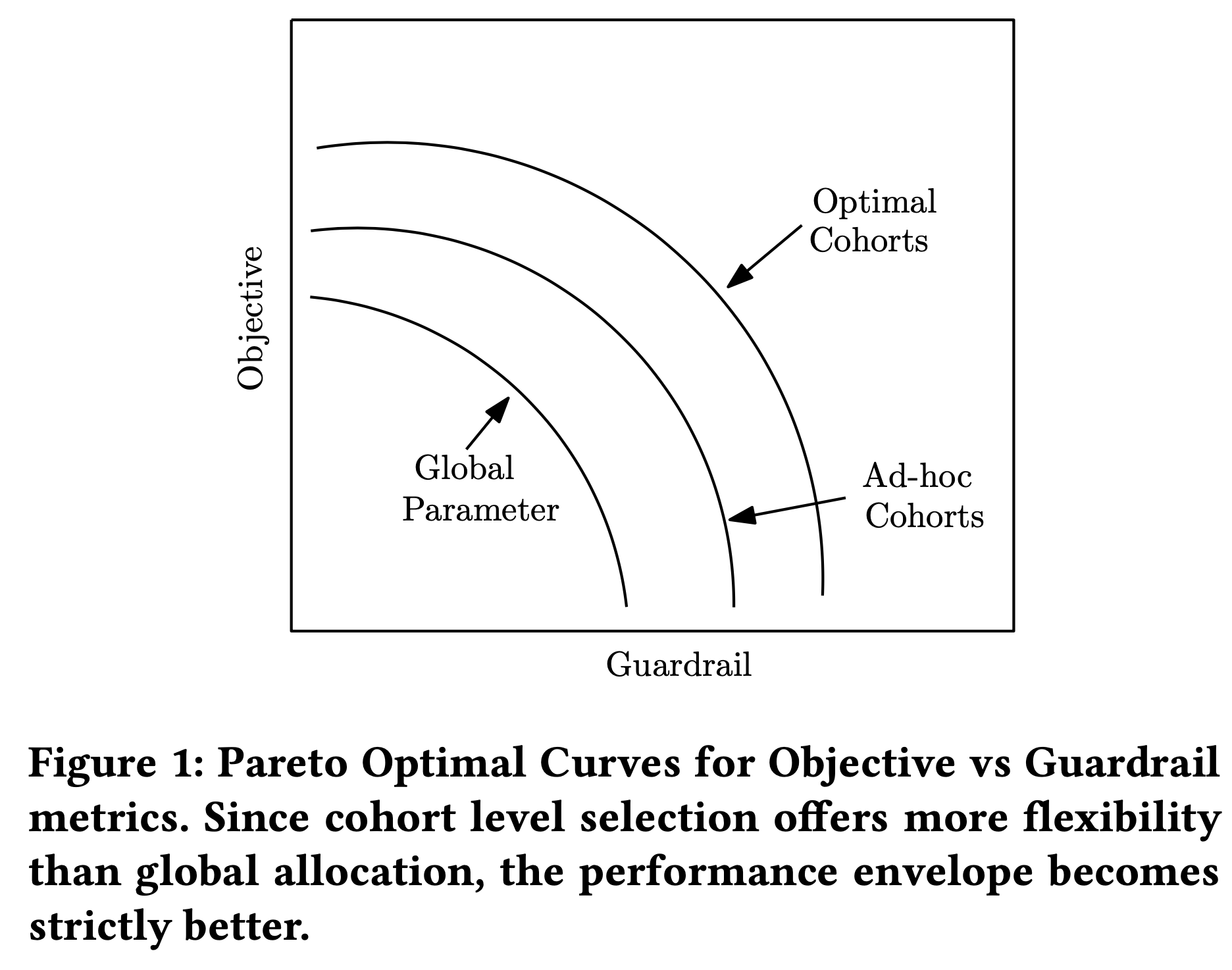
Pareto Optimal Curves for Objective vs Guardrail metrics

如上图所示，通过更个性化干预的选择，可以将帕累托前沿向前推。此处需要说明，并不是所有的场景都需要个性化干预选择，比如说需要考虑用户体验的稳定性和一致性，或者是用户对于产品的心智教育，这样的场景上更加适合全局分配。

本文中，我们假设我们可以进行用户粒度的随机试验，尝试多种不同的干预，并观测到用户级别的指标变化，如点击、评论、浏览等等。

本文的主要贡献有：

提出了一个通过估计异质处理效应并求解最优化问题，来做用户粒度最优干预的选择的框架
讨论了如何在我们所提出的技术方案中，根据使用场景来进行选择
介绍了一种新的合并tree的算法，来解决多treatment和多metric的问题，并用一种随机近似的方式，考虑因果效应估计的方差的同时，求解多目标优化问题
做了仿真实验，证明不同场景下，我们所提出框架的有效性
介绍了在实际产品中，我们系统的整体架构
在真实应用中取得了显著受益

解决方法

符号定义

先做一些符号定义，一共有$J$种干预，观测$K+1$个指标，其中有一个主要指标和$K$个观测指标，用$C_1,\cdots,C_n$表示对于某种干预在$K+1$个指标上存在异质性的用户群体，对于用户级别的场景，$C_i$仅包含一个用户，$n$则代表总用户数。对于每个群体$C_i$，用$U_{i,j}^k$表示采用干预$j$后，在指标$k$上的处理效应。更进一步，我们假设$U_{i,j}^k$是搞死随机变量，均值为$\mu_{i,j}^k$，方差为$\sigma_{i,j}^k$，对于每个指标$k$，用$\mathrm{U}_k$表示向量化的$U_{i,j}^k$，其中$i=1,\cdots,n$，$j=1,\cdots J$，简写为 \[ \mathrm{U}_k \sim \mathrm{N}_{n,J}\big(\mu_k,\text{Diag}(\sigma_k^2) \big) \]

我们希望保持其他贯彻指标不变条件下，最优化我们最关注的主要指标 \[ \begin{aligned} \max &&& \mathrm{x}^\mathsf{T} \mathrm{U}_0 \\ \text{s.t.} &&& \mathrm{x}^\mathsf{T} \mathrm{U}_k \leq c_k & \forall k=1,\cdots K \\ &&& \sum_jx_{i,j} = 1 & \forall i\\ &&& 0\leq \mathrm{x} \leq 1 \end{aligned} \] 其中$c_k$是某个指标的阈值。整个问题可以整理为两步：

基于随机试验来构建异质性群体，并估计处理效应$\mathrm{U}_k$
求解上述最优化问题，找出最优的干预分配方式$\mathrm{x}^*$

异质性估计

群体异质性

为了获得群体异质性的估计，文中采用Susan Athey的Causal Tree对用户群体进行划分，落在不同叶子结点的用户划分成不同的群组，$C_1^{j,k},\cdots,C_n^{j,k}$。

如何将多个treatment和metric划分的群组进行合并组合，是一个很有挑战的问题。大部分已有的方法会将这些群体分成很小的子集，但是这样会使得估计的处理效应非常不稳定，为了避免这个问题，我们采用原有组内的异质性估计。我们采用如下算法对不同用户群体进行归并，为了简化标记，我们用$l$表示$j,k$的组合

合并的结果是不同treatment和metric分割出的群体，相交没有子集，以及每个子群体对应的treamtent和metric下的异质性估计的均值和方差 \[ S_\text{out}=\big\{ \cap_{j=1}^J\cap_{k=0}^K C^{i,j}\neq \varnothing|C^{j,k}\in S_{j,k} \big\} \\ T_\text{out} = \big\{ (U_{j,k}(C),\sigma^2(C))| C\in S_\text{out},j=1,\cdots,J,k=0,\cdots K \big\} \]

这边我个人感觉这个算法写的不是很清楚，按我的理解：

Algo1中11行应该在12、13行之后

互斥子群体，应该也是两两之间相交为空集，而不是所有相交为空集

最后输出的，所有子群体，每个子群体都是所有treatment和metric分割下的交集，其关于某个treamtnet下对某个metric的异质性估计，是来自原有分割下整个群体的估计。

举个例子，一共10个用户，1234567890，原有分割为

j=1，k=1时，123，456，78，90，异质性估计1，2，3，4

j=1，k=2时，1，23，456，7890，异质性估计6，7，8，9

第一轮迭代后，输出结果为1，23，456，78，90

归并后人群关于j=1，k=1的估计为 1，1，2，3，4

归并后人群关于j=1，k=2的估计为6，7，8，9，9

个体级别异质性

采用了两种模型：

Causa Forest，
Two-Model建模

优化

因为目标函数和约束条件都是不确定的，包含若干随机变量，我们将该问题重写为 \[ \begin{aligned} \max &&& f(\mathrm{x})=\mathbb{E}(\mathrm{x}^\mathsf{T}\mathrm{U}_0) \\ \text{s.t.} &&& g_k(\mathrm{x}):= \mathbb{E}(\mathrm{x}^\mathsf{T}\mathrm{U}_k-c_k) \leq 0 & \forall k=1,\cdots K\\ &&& \sum_j x_{i,j}=1 &\forall i \\ &&& 0\leq \mathrm{x} \leq 1 \end{aligned} \] 我们有两种方式解决上述问题：

把整个问题当成纯随机优化问题，
可以用历史平均作为期望，将整个问题当作确定优化问题

随机优化

对于随机优化的求解，本文采用CSA算法（Coordinated Stochastic Approximation），问题重写为 $$ \[\begin{aligned} \max &&& f(\mathrm{x}):=\mathbb{E}_{\mathrm{U}_0} \big(F(\mathrm{x},\mathrm{U}_0)\big) \\ \text{s.t.} &&& g_k(\mathrm{x}):= \mathbb{E}_{\mathrm{U}_k} \big(G_j(\mathrm{x},\mathrm{U}_k)\big)\leq 0 & \forall k=1,\cdots K\\ &&& x \in \mathcal{X} \\ \end{aligned}\]

$$ 其中$\mathcal{X}$表示确定性约束。

CSA是一个迭代算法，需要迭代$N$步，在第$t$次迭代中，对约束条件进行估计 \[ \hat{G}_{k,t}=\frac{1}{L}\sum_{l=1}^L G_k(\mathrm{x}_t,\mathrm{U}_{k,l}) \] 如果所有估计的约束条件$\hat{G}_{k,t}$都小于阈值$\eta_{k,t}$，则选择目标函数的梯度方向$F'(\mathrm{x}_t,\mathrm{U}_{0,t})$更新，反之，从违反的约束条件集合中$\{k:\hat{G}_{k,t}>\eta_{k,t}\}$中随机选择一个$k^*$，沿其梯度方向$G'_{k^*}(\mathrm{x}_t,\mathrm{U}_{k^*,t})$进行更新，最终最优点是这些解的加权求和。

确定优化

确定优化的求解方式为SAA（Sample Average Approximation），即用样本期望作为随机变量的替代 \[ \begin{aligned} \max &&& f(x)=\mathrm{x}^\mathsf{T} \hat{\mu}_0 \\ \text{s.t.} &&& g_k(\mathrm{x}):=\mathrm{x}^\mathsf{T} \hat{\mu}_k - c_k \leq 0 & \forall k=1,\cdots K \\ &&& \sum_jx_{i,j} = 1 & \forall i\\ &&& 0\leq \mathrm{x} \leq 1 \end{aligned} \] 整个问题变成一个线性规划问题，有很多开源的solver都可以求解。

这种方式很简单快捷，但是无法利用随机变量方差的信息，在很多场景中，由于测量误差的存在（对于HTE估不准），会导致最终得到的解很大程度上违反了约束条件。

最优分配估计的偏差和方差

异质性的均值和方差都是未知的，在求解优化问题时，只能用样本估计的均值和方差来替代，所以这会使得估计最优分配的时候存在误差，而估计的偏差和方差可以通过bootstrap的方式得到。假设我们有$N$个用户，通过重采样的方式，抽出$N$个，重新求解确定优化或者随机优化问题，这些bootstrap得到的分配解，可以用来得到和原始分配的偏差以及方差。

在很多应用场景中，重采样是一个非常消耗计算的方法，假设在群组$C_i$中有$n_{i,j,treat}$个用户被施加了干预，有$n_{i,cont}$个用户为对照组，$n_i=n_{i,const}+\sum_jn_{i,j,treat}$，则方差为 \[ \Big(\hat{\sigma}_{i,j}^k\Big) =\Big(\hat{\sigma}_{i,j,treat}^k\Big)^2 + \Big(\hat{\sigma}_{i,const}^k\Big)^2 \] 重采样的均值服从$N\big(\hat{\mu}_{i,j}^k,(\hat{\sigma}_{i,j}^k)^2/n_i\big)$，方差服从$\Big(\hat{\sigma}_{i,j,treat}^k\Big)^2\cdot\mathcal{X}+ \Big(\hat{\sigma}_{i,const}^k\Big)^2 \cdot \mathcal{X}^{'}$，其中$\mathcal{X}$和$\mathcal{X}^{'}$是相互独立的chi方随机变量。相比于对于用户做重采样，bootstrap估计可以在多次模拟中得到，完整算法流程如下

整体算法

不同异质性处理方式和不同优化模型选择的优劣见下表

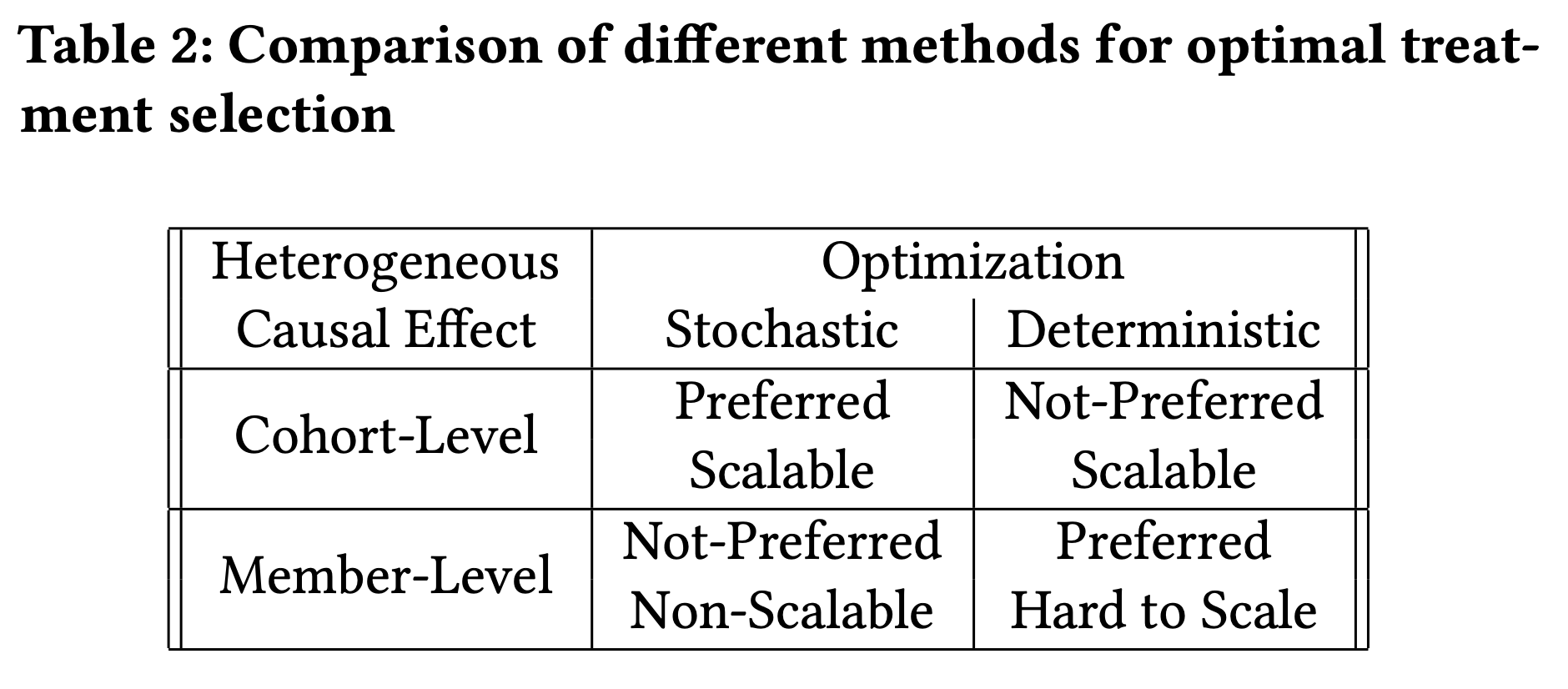
系统架构

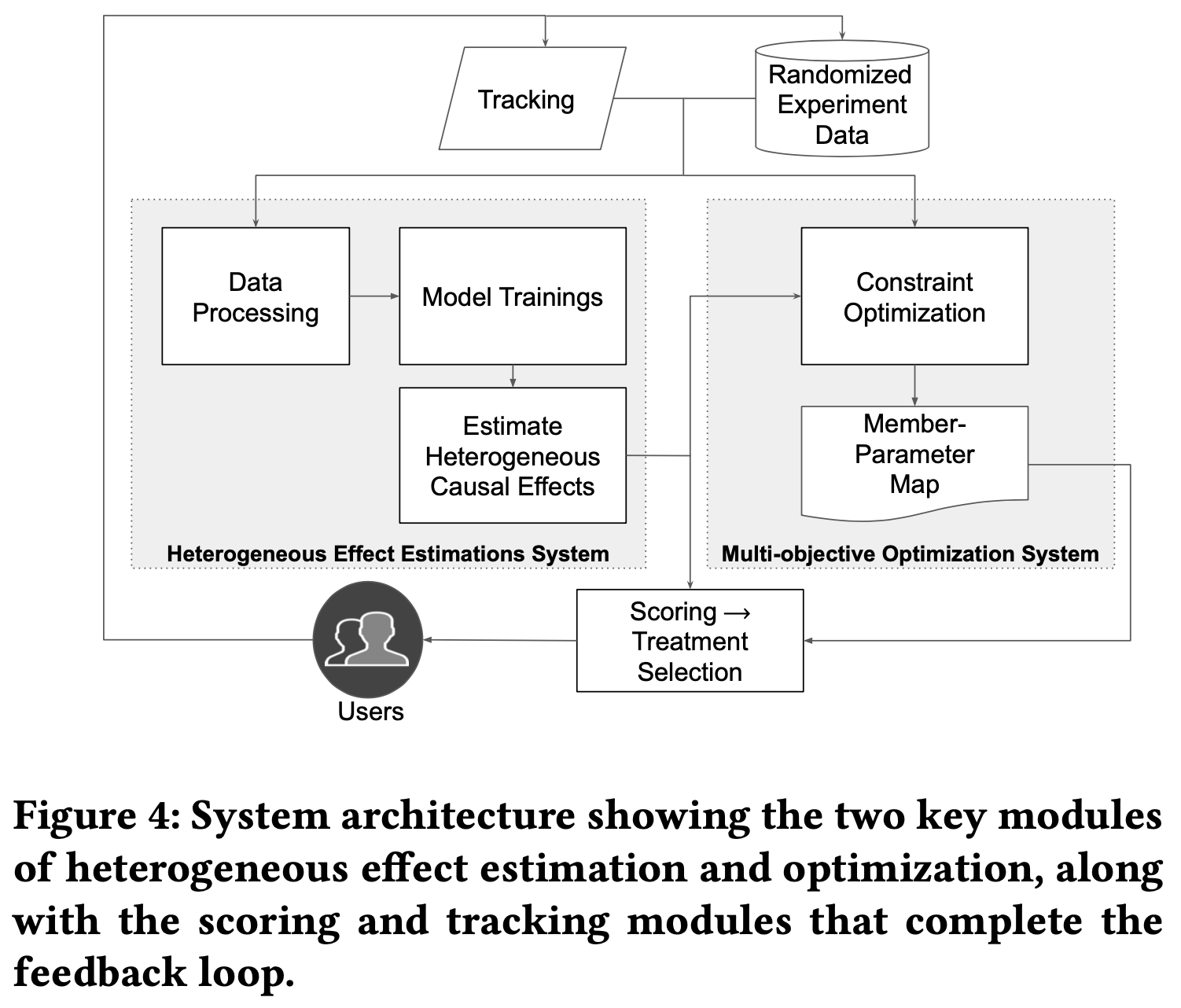
整个架构其实还比较中规中矩，相比一般系统会多随机实验数据处理以及优化求解部分，这个在相关场景下，大家的处理方式都差不多。

实验结果

仿真分析

文中构建了一份仿真数据来评测不同情况下算法的表现：

baseline为全局相同策略，Global
HT.ST，启发式群体划分，同时采用随机优化
CT.ST，用Causal Tree构建群组，采用随机规划
CF.DT，用Causal Forest估计个体异质性，然后采用确定性规划
TM.DT，用two-model的方式估计异质性，然后采用确定性规划

按照如下因果图随机生成数据，同时加入不确定性超参数来控制整个任务学习的难度

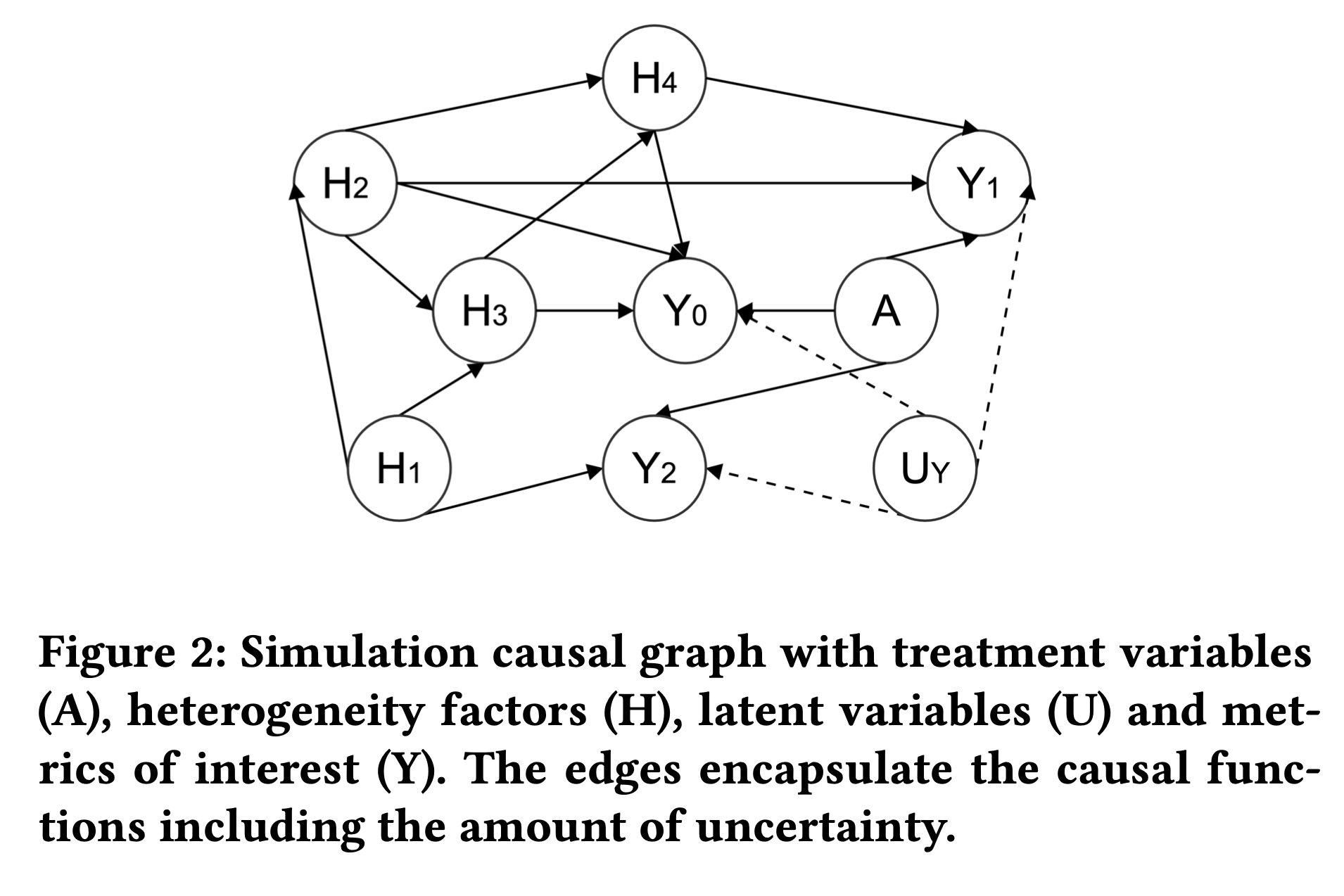
在优化问题中，我们希望最大化$Y_0$的lift，同时保证$Y_1$和$Y_2$的lift非负，对于HT.ST，生成了16个群组。对不不同的噪声水平（不确定性参数），计算不同方法所得到的最优解。指标$k$下标准化后的平均ITE \[ \tau(\mathrm{x}^*)_k=\frac{ \frac1n\sum_{i=1}^n\sum_{j=1}^3 (Y_{j,i,k} - Y_{0,i,k}) z_{i,j}^* }{\mu_{0,k}} \] 仿真中模拟了两个场景，分别是存在全局分配最优策略和个性化选择干预有更好结果的情形。

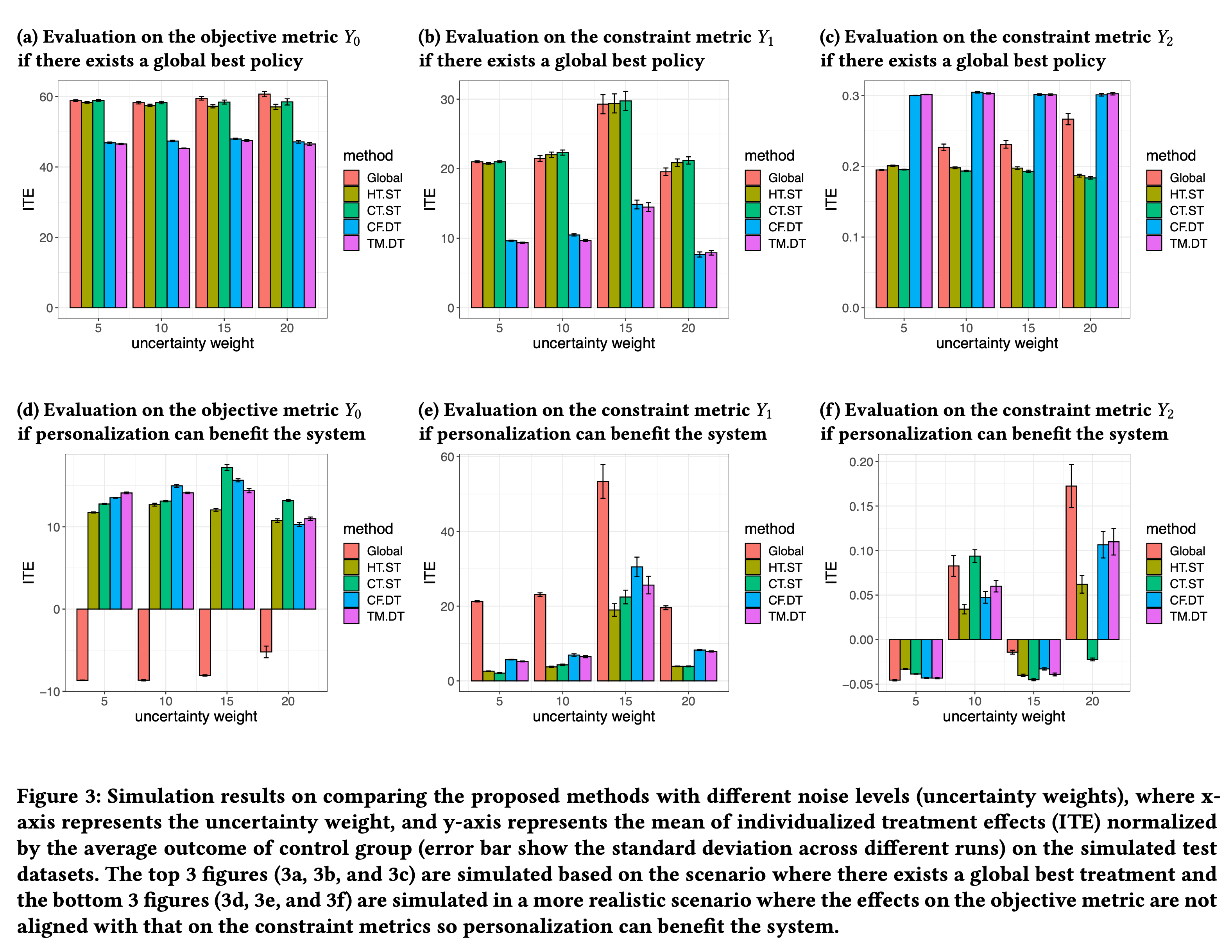
可以观察到：

随机优化会得到更好的结果，当存在全局最优干预时候，采用随机优化的方法，可以与最优解保持基本相同的水平，但是确定性规划的方法受到估计量高方差的影响，导致最终结果离最优解很远。
异质性估计和个性化带来的收益，对于后三张图，baseline策略，为了满足约束，会给出很差的结果，采用CF划分的群组会比启发式划分的群组有更好的结果。对于群体级别和个体级别的决策，在低噪声情况下，个体级别的决策会表现出更好的效果，但是随着噪声增加，方差增大，群体级别的决策会更占上风，随机规划对于高方差场景的处理会更好，算法整体鲁棒性更好。

实际业务场景

本文中提到实际上线应用的产品是LinkedIn的Notification System，为了避免过度打扰用户，会限制每天发送给用户的提醒数，但是不同用户会有不同偏好、广告承受度，相同的标准会导致一个次优的用户体验，所以我们希望能够个性化每个用户发放提醒的数量。

实际应用中，先小流量探测不同用户，收集了两周数据，特征考虑了：

用户属性，如国家区域、语言、工作职级等
干预相关特征，如过去提醒和邮件发送次数等
其他活动特征，如过去访问次数、点击、喜欢、分享、评论数
用户网络特征，如关注数和粉丝数

主要观测的指标：

Sessions数量，过去访问次数
Notification Sends，已经发送后的提醒数
Notification CTR，提醒的CTR
Total Disables，不喜欢提醒的数量

此处省略一下线上实验细节，在线实验结果

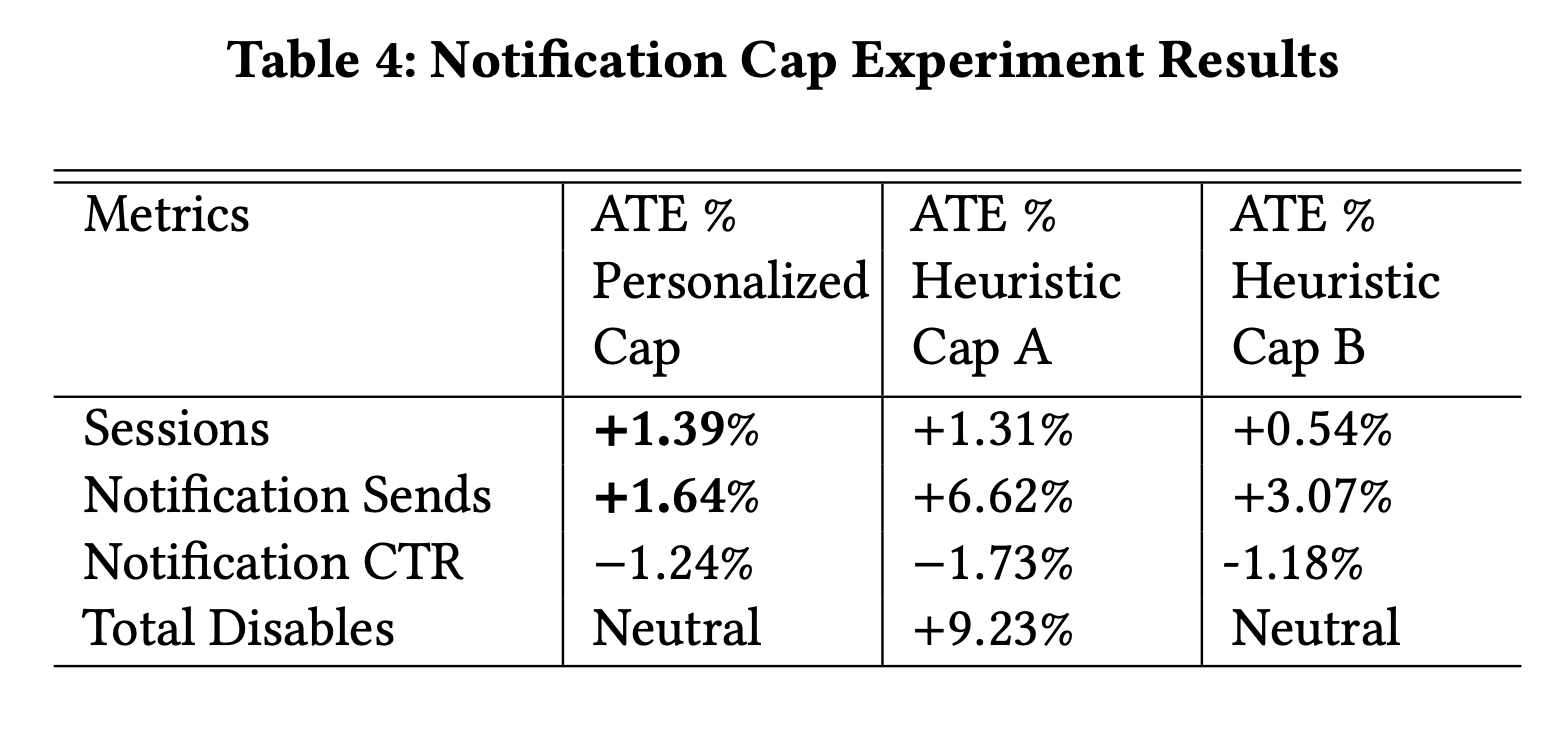
总结

文章整体写的“比较”扎实，是目前业界为数不多的、在HTE方面做的比较全面的工作，本文重点并没有放在如何得到更好的ITE or ATE的估计上，而是在整体框架以及优化求解策略上（虽然按我的经验来看，随机规划并没有在广泛业务场景中拿到收益，但这也可能是我之前打开方式不对），如果是这个方向想入门的同学，这的确是一篇值得精读一下的文章。

文中future work中也提到了一些目前业界共识的难题我也在此列出来：

收集随机实验数据的成本非常高，设计一个cost-efficient data collection framework 或者引入观测数据建模，是一个很重要的方向
用户会从不同的群组里进入或离开，也即动态多周期的决策，目前并没有过多考虑
如何直接面向多treatment、多metirc来生成分组，也是值得探索的