这篇文章仿佛是中了recsys2020,内容跟当前工作比较相关,所以拿出来写一写。
Introduction
现代在线旅游平台(OPT、)会提供各种产品和服务给旅行者,比如航班、住宿、地面交通等等,促销活动(promotion)如升舱、免费的午餐或者租车的折扣,都是非常常用的方式。一个促销活动应该有一个正向的平均处理效应(ATE,average treatment effect),比如说用户的增长或者满意度的提升,但是需要在一定的ROI(Return on Investment)约束下,ROI则是一个市场营销活动中常见的指标: \[ \text{ROI}=\frac{\Delta\text{Revenue} - \Delta\text{Investment}}{\Delta\text{Investment}} \] 为了确保促销活动是可持续的,ROI会有一个下限的约束,如\(\text{ROI}\geq0\),这就产生了一个促销活动花费和目标增量之间的权衡,一个很好的例子是,预定住宿的时候,一个促销活动经常会提供一顿免费的午餐作为补贴,只有当住宿预定率可以cover住提供免费午餐这额外的费用的时候,这个促销活动才是可持续的。
通过给一部分顾客提供促销活动,公司可以获得更多的价值,同时维持财务上的约束,来保证促销活动是可持续的。一个很流行的做法是选择出目标的用户群体,uplift model就是一个常用的建模方式,它可以估计出处理在产出上的期望因果效应,来辨识出哪些是自愿的买家,哪些是因为补贴行为才购买的顾客,这可以通过估计促销活动的条件平均处理效应(CATE,Conditional Average Treatment Effect)来实现,\(\text{CATE}_Y(x)\)被定义为条件下,是否购买概\(\text{Pr}(Y=1)\) 的增量。
本文中提出了一种新的建模方式,基于Retrospective Estimation(我也没查到资料这是个啥东西。。),仅依赖于正例样本。主要贡献有以下几点:
- 对于uplift和ROI约束的优化框架
- Retrospective Estimation,仅依赖于数据中的正例样本
- 线上动态模型校准
- 大规模的线上实验验证
Problem Formulation
我们关注于最大化完成交易的用户数量,同时决定是否提供促销款,来满足全局约束\(\text{ROI}\geq 0\),\(Y\)表示是否完成交易,\(R\)表示完成交易的收益,\(C\)表示促销活动的成本,我们假设,没有完成交易的话,就没有收益和成本。
对于一个用户\(i\),\(Y_i(1)\)表示当用户\(i\)被给予一个促销活动\(T=1\)时的潜在购买,相似的也有\(R_i(1)\)和\(C_i(1)\),与之相反的有\(Y_i(0)\)、\(R_i(0)\)和\(C_i(0)\)。我们定义每个变量上的的CATE: \[ \begin{aligned} \text{CATE}_Y(x)=\mathbb{E}[Y_i(1)-Y_i(0)|X_i=x]\\ \text{CATE}_R(x)=\mathbb{E}[R_i(1)-R_i(0)|X_i=x]\\ \text{CATE}_C(x)=\mathbb{E}[C_i(1)-C_i(0)|X_i=x]\\ \end{aligned} \] 我们定义利润为\(\Pi_i=R_i-C_i\),损失为\(\cal{L}=-\Pi\), \[ \text{CATE}_\Pi(x) = \text{CATE}_R(x)-\text{CATE}_C(x)=-\text{CATE}_\cal{L}(x) \] 我们的目标就是找到一个函数\(F\),对于给定\(x\),决定是否给一个客户提供促销活动,同时最大化总的增加的交易,在ROI的约束下。
我们用一个分数函数\(g\)和阈值\(\theta\)来建模这个函数\(F\),\(\mathbb{I}[g(x)\geq\theta]\),用\(z_i\in\{0,1\}\)表示是否给用户\(i\)促销活动,则有
\[ \begin{aligned} \max && \sum_{i\in U} z_i\cdot \text{CATE}_Y(x_i) \\ \text{s.t.} && \sum_{i\in U}z_i \cdot \text{CATE}_{\cal{L}}(x_i)\leq 0 \end{aligned} \]
其中目标函数为最大化总的teatment effect,约束为条件期望损失非正,等价于ROI非负。
我们由上面式子可以推导出,\(\text{CATE}_Y\leq0\Rightarrow\text{CATE}_{\cal{L}}\geq0\),因为收益只可能来自于额外完成的交易。用贪婪算法可以简单的解决这个背包问题,我们可以近似的根据\(\frac{\text{CATE}^i_Y}{\text{CATE}_{\cal{L}}^i}\)对用户\(U\)排序,对满足ROI约束的用户群体可以增加促销活动。用\(j\)表示最后一个施加促销活动的用户,我们可以定义\(g(x)=\frac{\text{CATE}_Y(x)}{\text{CATE}_{\cal{L}}(x)}\)和阈值\(\theta^*=\frac{\text{CATE}_Y^j}{\text{CATE}_{\cal{L}}^j}\),我们可以用上述规则来决策以后对谁来增加促销活动。这个框架将问题简化为学习\(\frac{\text{CATE}_Y(x)}{\text{CATE}_{\cal{L}}(x)}\)、\(\text{sign}[\text{CATE}_Y(x)]\)和\(\text{sign}[\text{CATE}_{\cal{L}}(x)]\)。
Method For Uplift Modeling Under ROI Constraints
文中主要对比了4种方式:
- Two-Model,分别对有无treatment建模
- Transformed outcome,单个模型估计\(\text{CATE}_Y(x)\)
- Fractional Approximation,贪婪排序,依赖于Two-Models产出的\(-\frac{\text{CATE}_Y(x)}{\text{CATE}_{\cal{L}}(x)}\)
- Retrospective Estimation,直接估计分数函数,只依赖于正例样本
文中所有的建模都依赖于随机实验的数据,随机实验的数据使得\(\mathbb{E}[Y_i(1)|X_i=x]=\mathbb{E}[Y_i|T_i=1,X_i=x]\),模型都采用xgboost模型,历史数据由100millions+。
定义\(\hat{C}(x)=\mathbb{E}[C|x,T=1,Y=1]\)和\(\hat{R}_t(x)=\mathbb{E}[R|x, T=t, y=1]\),则\(\frac{\text{CATE}_Y(x)}{\text{CATE}_{\cal{L}}(x)}\)可以写为 \[ \frac {\text{Pr}(Y=1|x, T=1)-\text{Pr}(Y=1|x, T=0)} {\text{Pr}(Y=1|x,T=1)[\hat{C}(x)-\hat{R}_1(x)]+\text{Pr}(Y=1|x,T=0)\hat{R}_0(x)} \] Retrospective Estimation,我们可以将下式写为 \[ \text{Pr}(Y=1|x, T=1)=\frac{\text{Pr}(T=1|x,Y=1)\text{Pr}(Y=1|x)}{\text{Pr}(T=1|x)} \] 其中分母是treatment propensity,我们可以设置为0.5。分母并不允许我们直接估计\(\text{CATE}_Y(x)\),但是提供了\(\text{Pr}(Y=1|x,T=1)\)和\(\text{Pr}(Y=1|x,T=0)\)的比例的表达式 \[ \frac{\text{Pr}(Y=1|x,T=1)}{\text{Pr}(Y=1|x,T=0}=\frac{\text{Pr}(T=1|x,Y=1)}{1-\text{Pr}(T=1|x,Y=1)}=\frac{S(x)}{1-S(x)} \] 此处\(S(x)=\text{Pr}(T=1|x,Y=1)\)表示受到促销活动\(T=1\)中的正例概率。所以有 \[ \begin{aligned} \frac{\text{CATE}_Y(x)}{\text{CATE}_{\cal{L}}(x)}=&\frac {2S(x)-1} {S(x)[\hat{C}(x)-\hat{R}_1(x)]+[1-S(x)]\hat{R}_0(x)}\\ \text{sign}[\text{CATE}_Y(x)]=&\text{sign}[S(x)-0.5]\\ \text{sign}[\text{CATE}_{\cal{L}}(x)]=&\text{sign}[\frac{\hat{R}_1(x)}{2\hat{R}_1(x)-\hat{C}(x)}S(x)]\\ \end{aligned} \] 其中估计\(S(x)\)、\(\hat{R}_1(x)\)、\(\hat{R}_0(x)\)和\(\hat{C}\)都只需要正例样本,这样可以避免大部分无用数据,同时解决样本不平衡的问题。如果我们假设每次预定的成本和收益都独立于\(x\),同时每次预定的收益独立于treatment \(T\),\(\hat{R}_t(x)=\hat{R},\hat{C}(x)=\hat{C}\),那么有 \[ \frac{\text{CATE}_Y(x)}{\text{CATE}_{\cal{L}}(x)}=\frac {2S(x)-1} {S(x)[\hat{C}-\hat{R}]+[1-S(x)]\hat{R}} \] 那么可以推导出,当\(S(x)<\frac{\hat{R}}{2\hat{R}-\hat{C}}\)时,\(\text{CATE}_{\cal{L}}(x)>0\),当\(S(X)>0.5\)时,\(\text{CATE}_Y(X)>0\)。这使得我们可以只对\(S(X)=\text{Pr}(T=1|x,Y=1)\)建模。
离线情况下,我们是可以找到\(g\)和\(\theta\),但是在线环境中,\(\theta\)可能会改变,文中提出了一种简单的曲线拟合的方法来解决这个问题,我们你和这个ROI曲线,来动态的修正\(\theta\)。
对于评估,文中采用Qini Curve和ROI Curve
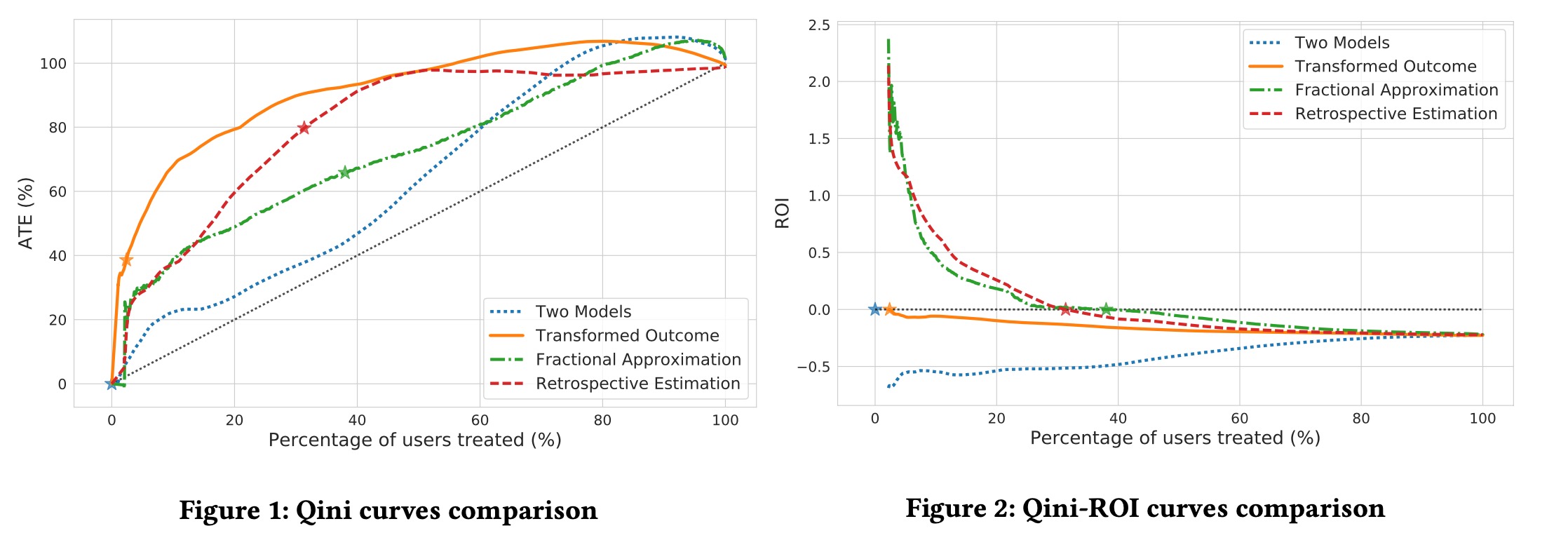
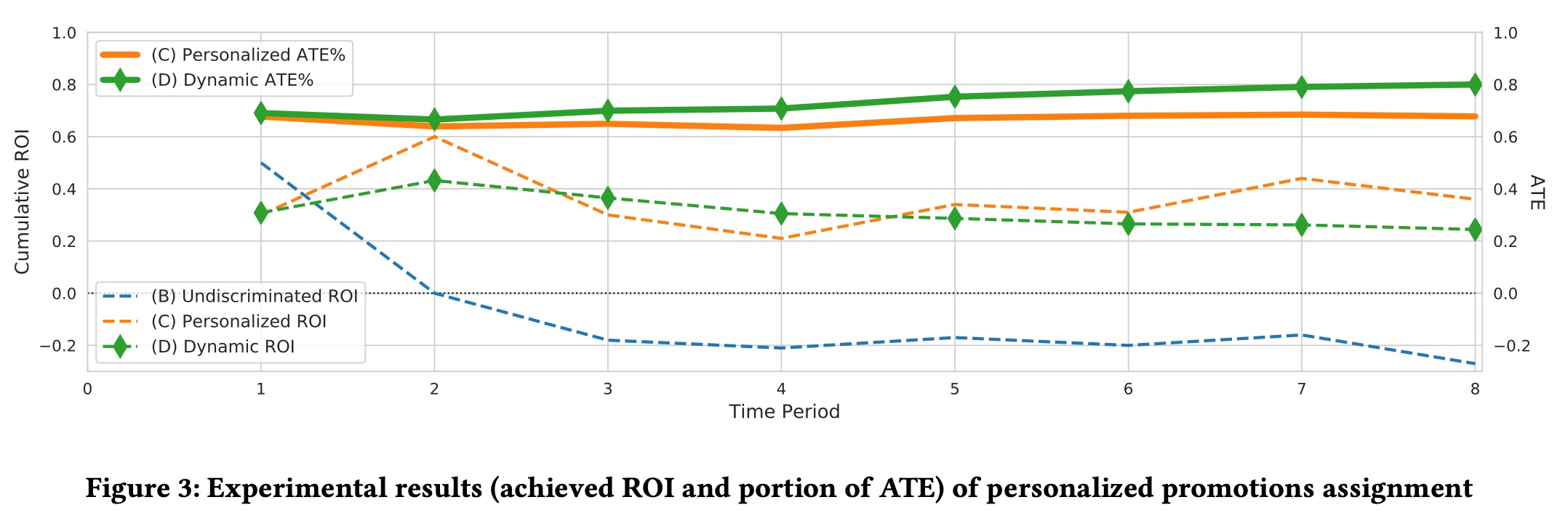
通过ROI Curve找到ROI=0的点,然后在Qini Curve上找到对应的ATE。
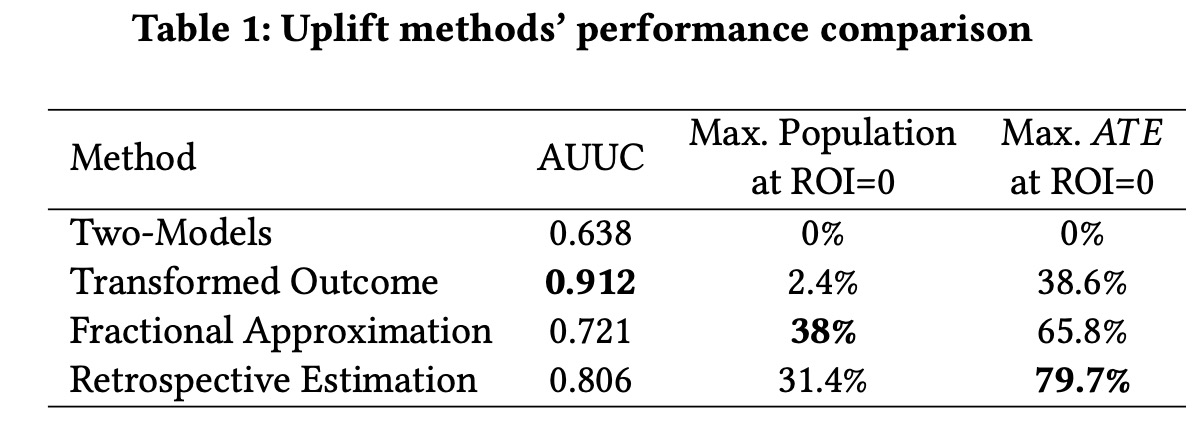
实验结果暂时列这里,感兴趣的同伴看原文,也太深我也要早些休息了。