TL;DR,
预算约束+效率成本约束下,最优广告出价策略,双PID在线调节超参数(对偶变量)
摘要
Real-Time Bidding (RTB) is an important paradigm in display advertising, where advertisers utilize extended information and algorithms served by Demand Side Platforms (DSPs) to improve advertising performance. A common problem for DSPs is to help advertisers gain as much value as possible with budget constraints. However, advertisers would routinely add certain key performance indicator (KPI) constraints that the advertising campaign must meet due to practical reasons. In this paper, we study the common case where advertisers aim to maximize the quantity of conversions, and set cost-per-click (CPC) as a KPI constraint. We convert such a problem into a linear programming problem and leverage the primal-dual method to derive the optimal bidding strategy. To address the applicability issue, we propose a feedback control-based solution and devise the multivariable control system. The empirical study based on real-world data from Taobao.com verifies the effectiveness and superiority of our approach compared with the state of the art in the industry practices.
实时竞价(RTB)是展示广告领域的一个重要形式,广告主利用需求方平台(DSP)提供的额外信息和算法来提高广告效果。
DSP的一个常见问题是帮助广告主在预算约束下获得尽可能多的价值。现实情况中,广告主也会为广告计划增加一些KPI约束。
在本文中,我们研究了一种常见的情况,即广告商主以转换数量最大化为目标,并将每次点击成本(CPC)作为KPI约束。我们将这样的问题建模为线性规划问题,并利用原始对偶方法得出最优竞价策略。为了解决适用性问题,我们提出了一个基于反馈控制的解决方案并设计了多变量控制系统。
基于淘宝实际数据的实证研究验证了我们的方法与行业实践中的技术现状相比具有有效性和优越性。
问题背景
在RTB的场景下,广告主除了关心预算的消耗情况外,同样关心一些效率指标,如CPM或者CPC,之前的方法都没有考虑这种约束,本文提出一种同时兼顾预算消耗约束和效率成本约束(CPC)的最优出价策略,帮助广告主最大化转化收益。
解决方法
假设一天存在\(N\)次竞价机会,每次竞价对于广告主而言都有不同的价值\(v_i\),基于价值\(v_i\),广告主会出价\(\text{bid}_i\)参与拍卖,每个曝光竞价都有有一个胜利价格\(\text{wp}_i\),\(\text{wp}_i\)是所有广告主的第二高出价(GSP机制下),如果出价\(\text{bid}_i\)高于\(\text{wp}_i\), 则会按照\(\text{wp}_i\)收费,如果竞得则\(x_i=1\),反之\(x_i=0\)。总收益和总成本为 \[ \text{Value} = \sum_i x_i\cdot v_i \\ \text{Cost} = \sum_i x_i\cdot \text{wp}_i \] CPC成本记作 \[ \text{CPC} = \frac{\sum_i x_i \cdot \text{wp}_i}{\sum_i x_i \cdot \text{CTR}_i} \] 当我们关心\(v_i\)是转化情况的时候,\(v_i=\text{CTR}_i \cdot \text{CVR}_i\),整个问题建模为 \[ \begin{aligned} \max && \sum_i x_i \cdot \text{CTR}_i \cdot \text{CVR}_i \\ \text{s.t.} && \sum_i x_i \cdot \text{wp}_i \leq B\\ && \frac{\sum_i x_i \cdot \text{wp}_i}{\sum_i x_i \cdot \text{CTR}_i} \leq C \\ && 0\leq x_i \leq 1,\forall i \end{aligned} \] 上式是一个线性规划问题,可以通过找到最优的\(x_i\)来得到满足约束条件情况下、最大化的目标函数,存在很多方式可以求解这个问题,但是我们想要的是最优的竞价策略而不是分配策略,即我们并不关心\(x_i\)的取值,更关注于什么样的竞价策略会影响\(x_i\) 。基于这种考虑,我们采用原始对偶法,通过将原问题转化成对偶问题以及考虑原问题的解和对偶问题的解存在互补松弛性,获得最优的竞价策略。
对偶问题写作 \[ \begin{aligned} \min && B\cdot p + \sum_i r_i \\ \text{s.t.} && \text{wp}_i \cdot p + (\text{wp}_i - \text{CTR}_i\cdot C)\cdot q +r_i \geq v_i && \forall i \\ && p\geq 0 \\ &&q\geq 0 \\ &&r_i \geq 0 &&\forall i \\ && v_i=\text{CTR}_i \cdot \text{CVR}_i && \forall i \end{aligned} \] 原问题最优解为\(x_i^*\),对偶问题最优解为\(p^*,q^*,r_i^*\),根据互补松弛性,有 \[ x_i^* \cdot \Big( v_i - \text{wp}_i \cdot p^* - (\text{wp}_i - \text{CTR}_i \cdot C) \cdot q^* - r_i^* \Big) = 0, \forall i\\ (x^*_i - 1) \cdot r_i^* = 0, \forall i \] 当\(x_i=1\)竞得时 \[ \begin{aligned} v_i - \text{wp}_i \cdot p^* - (\text{wp}_i - \text{CTR}_i \cdot C) \cdot q^* - r_i^* &= 0\\ v_i - \text{wp}_i \cdot p^* - \text{wp}_i \cdot q^* + \text{CTR}_i \cdot C \cdot q^* &= r_i^* \\ v_i - \text{wp}_i \cdot (p^* +q^*) + \text{CTR}_i \cdot C \cdot q^* &= r_i^* \\ \end{aligned} \] 当\(x_i^*=0\)非竞得时,\(r_i^*=0\)。
假设我们设定最优竞价策略为 \[ \begin{aligned} \text{bid}_i^* &= \frac{1}{p^*+q^*} \cdot v_i + \frac{q^*}{p^*+q^*} \cdot \text{CTR}_i \cdot C \\ &=\frac{1}{p^*+q^*} \cdot \text{CTR}_i\cdot \text{CVR}_i + \frac{q^*}{p^*+q^*} \cdot \text{CTR}_i \cdot C \end{aligned} \] 下式成立 \[ x_i^* \cdot \Big( (\text{bid}_i^* - \text{wp}_i)\cdot(p^* +q^*) - r_i^* \Big) = 0, \forall i\\ \] 如果\(x_i^*=1\),那么 \[ \begin{aligned} &(\text{bid}_i^* - \text{wp}_i)\cdot(p^* +q^*) - r_i^* \\ =& \Big( \frac{1}{p^*+q^*} \cdot \text{CTR}_i\cdot \text{CVR}_i + \frac{q^*}{p^*+q^*} \cdot \text{CTR}_i \cdot C - \text{wp}_i \Big) \cdot (p^* +q^*) - r_i^* \\ =& \text{CTR}_i\cdot \text{CVR}_i + \text{CTR}_i \cdot C\cdot q^* - \text{wp}_i \cdot (p^* +q^*) - r_i^* \\ =&0 \end{aligned} \] 其中\(p,q,r_i\geq0,\forall i\),所以\(\text{bid}_i^*-\text{wp}_i\geq0\),如果\(x_i^*=0\),\(r_i^*=0\),由对偶问题中的约束\(\text{wp}_i \cdot p + (\text{wp}_i - \text{CTR}_i\cdot C)\cdot q +r_i \geq v_i\)有\(\text{bid}_i^*-\text{wp}_i\leq 0\),所以这种出价策略能够使得竞得时,出价高于胜出价格,不竞得的时候,出价低于胜出价格。
有了最优出价策略后,剩下问题是如何得到最优的\(p^*\)和\(q^*\)。实际上,通过求解线性规划原问题和对偶问题都可以得到最优的结果,但是需要知道所有的竞价信息,包括每条流量的竞得价格、CTR、CVR的预估,同时由于环境的变动,采用历史数据可能无法得到当前环境的下的最优解,而我们需要在每个广告计划开始前确定竞价策略,所以本文提出了一种双变量控制的方法。
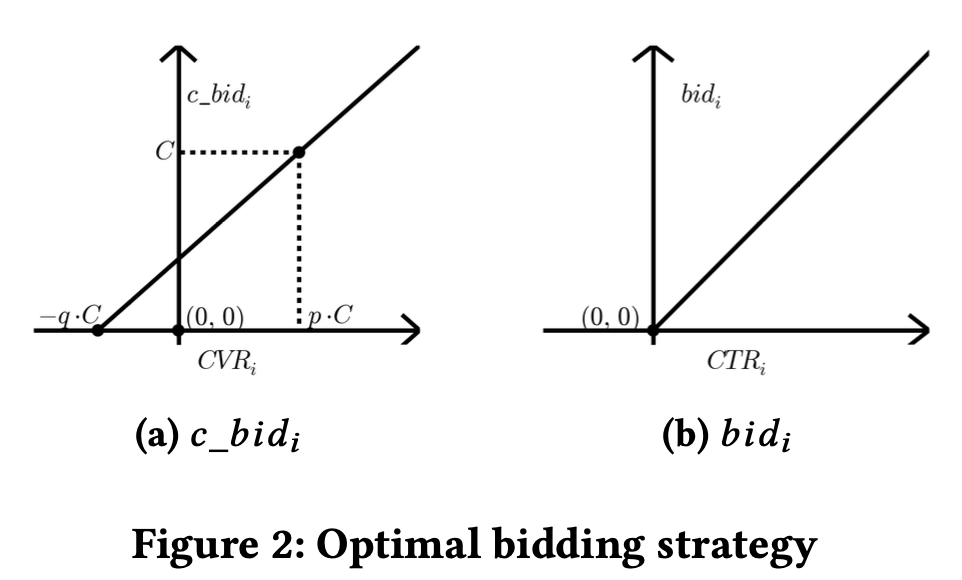
将出价策略拆分成两个阶段,\(\text{c\_bid}_i\)可以看作每次点击的出价,当每次竞价请求来的时候,我们优先确定单次点击的出价,最终出价由\(\text{c\_bid}_i\)乘以\(\text{CTR}_i\)得到。由于广义二价拍卖机制(GSP)的存在,点击的成本不会高于点击的出价,所以\(\text{c\_bid}_i\)直接影响CPC成本。 \[ \begin{aligned} \text{c\_bid}_i &= \frac{1}{p+q} \cdot\text{CVR}_i + \frac{q}{p+q} \cdot C \\ \text{bid}_i &= \text{c\_bid}_i \cdot \text{CTR}_i \\ &= \Big(\frac{1}{p+q} \cdot\text{CVR}_i + \frac{q}{p+q} \cdot C\Big) \cdot \text{CTR}_i \\ \end{aligned} \] 有几点值得注意的:
- 点击的出价,线性正比于转化率
- 点击出价的线会过两点,如下图所示,\((p\cdot C, C)\)和\((-q\cdot C, 0)\)
- 并不过原点,也好理解,在单位点击成本约束下,如果我们想对高转化的商品出更高的价格,必然需要用较少的出价来竞得一些“垃圾”流量
反馈系统通过系统输出来调整输入,以达成目标效果。在我们的场景中,竞价策略和RTB环境作为一个动态系统,超参数\(p\)和\(q\)作为系统的输入,这样整个问题就变成了一个前向反馈控制系统。我们的目标首先是希望最大化广告的价值,并且控制CPC成本,其次我们需要在时间维度上平滑预算,尽可能赢得有价值的展示机会。
反馈系统设计如下图所示
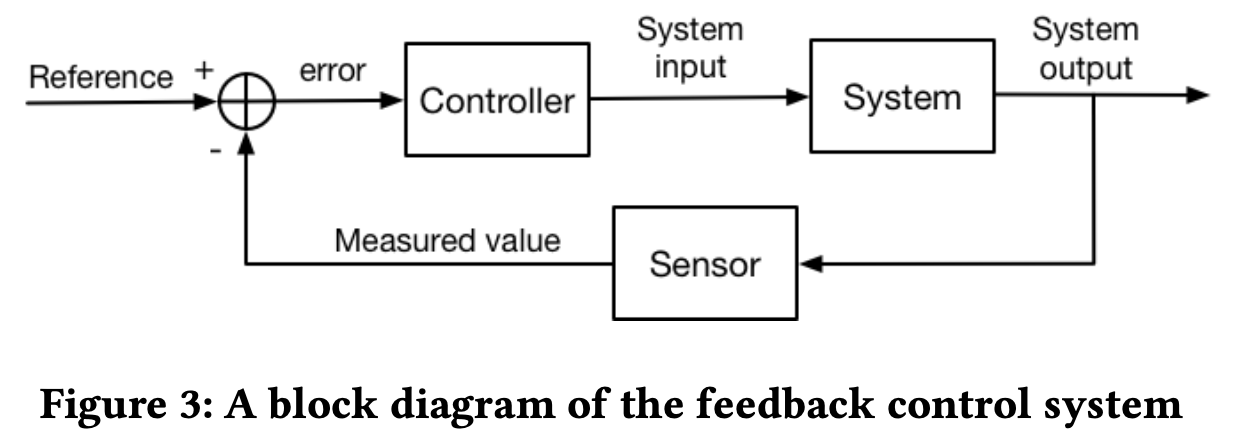
本文中我们采取PID作为反馈控制器,其通过连续计算误差\(e(t)\)来产生控制信号\(u(t)\),其中\(k_p,k_i,k_e\)为PID超参数,\(r(t)\)是系统输入,\(y(t)\)是系统输出 \[ \begin{aligned} e(t) &= r(t) - y(t)\\ u(t) &= k_p \cdot e(t) + k_i \sum_{i=1,\cdots t} e(i) + k_d\cdot\big(e(t) - e(t-1)\big) \\ x(t+1) &= \phi\big(x(0), u(t)\big)\\ \end{aligned} \] 我们已经把出价策略问题转化为一个前向反馈控制问题,如何通过调整\(p\)和\(q\)来同时控制预算的消耗和CPC成本是目前的难题。由于多个输入和多个输出的存在,我们没有办法直接使用PID算法。当然也存在一些解决多输出、多输出的PID衍生算法,本文并不在此讨论,下面着重介绍如何从最优的竞价策略出发来设计多变量控制系统。
上图展示了固定\(q\)时,随着\(p\)从\(0\)到\(\infty\),出价线围绕\((-q\cdot C,0)\)点做顺时针旋转,当\(p=\infty\)时,广告计划的出价为\(0\),此时受到预算约束,不能再多花钱,当\(p=0\)时说明预算并不是生效的约束,但是由于CPC约束的存在,出价并不会变成无穷大,竞价策略的斜率由\(q\)决定。我们认为参数\(p\)对于调节预算而言,非常直接有效,可以降低预算消耗速度。
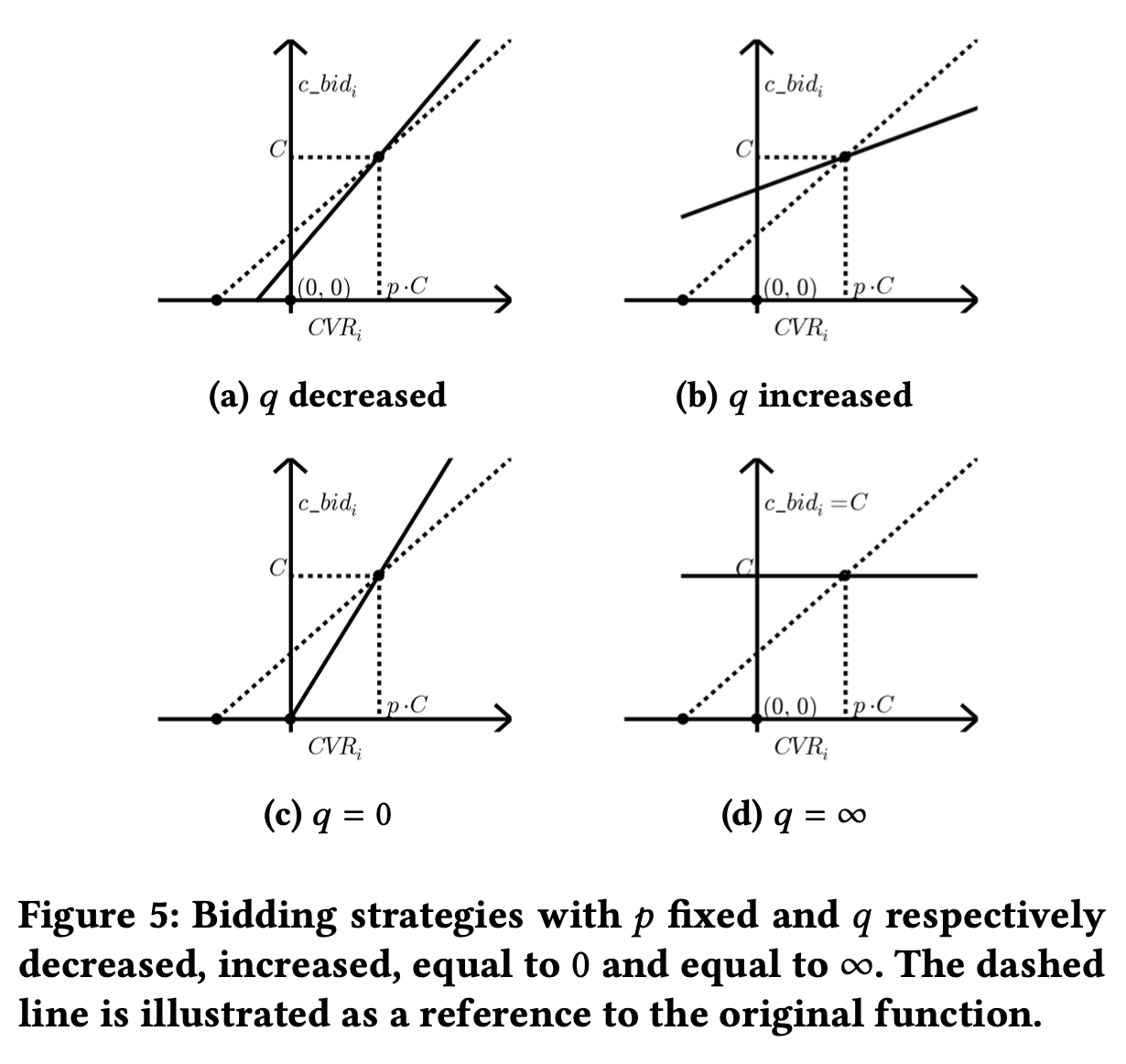
与之相似,我们固定\(p\)看\(q\)变化的影响,随着\(q\)从\(0\)到\(\infty\),出价线围绕\((p\cdot C,C)\)点做顺时针旋转,随着\(q\)增加,低于\(C\)成本的出价会更高,会赢得更多出价,高于成本C的出价会更低,赢得更少,这样会使得CPC更加倾向于低于C。当\(q=\infty\)时,出价必须等于CPC,当\(q=0\)时,CPC成本约束并不生效。
基于上述分析,我们认为\(p\)和\(q\)可以分别独立用于控制预算和成本,并将对方的变化视作外部的噪声,所以我们把多变量的控制问题转化成两个单变量的控制问题,此时就可以使用PID进行控制。
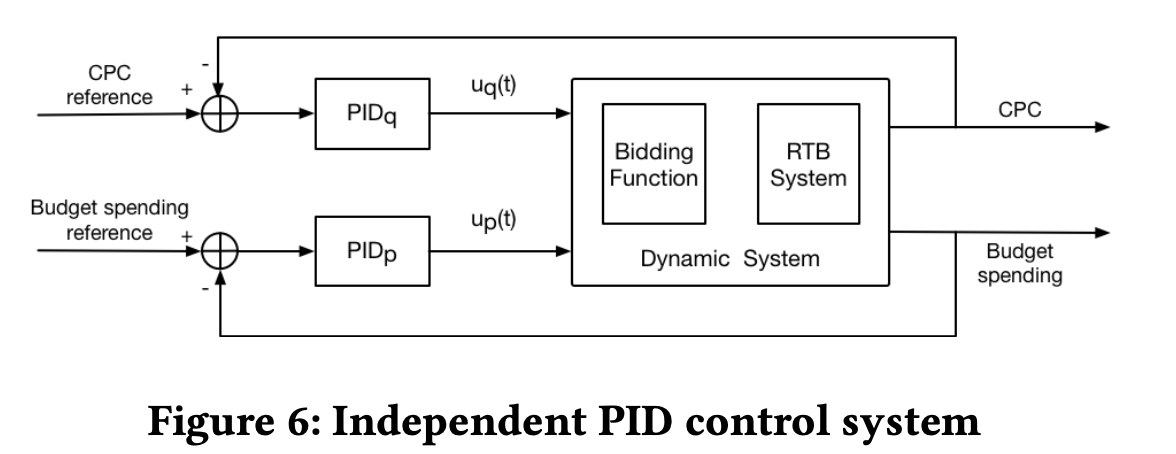
但是实际上\(p\)和\(q\)的变化,会影响成本和预算消耗。虽然PID可以将其视作环境系统的一部分,一定程度上减缓这种耦合效应的影响,但是这种耦合效应很难度量,同时我们对于整个动态系统并没有太多的了解,所以我们采用模型预测控制(Model Predictive Control)的思路尝试解决这个问题。值得一提的是,我们并没有想去建模RTB环境,而是结合人工知识,预测耦合效应的影响。
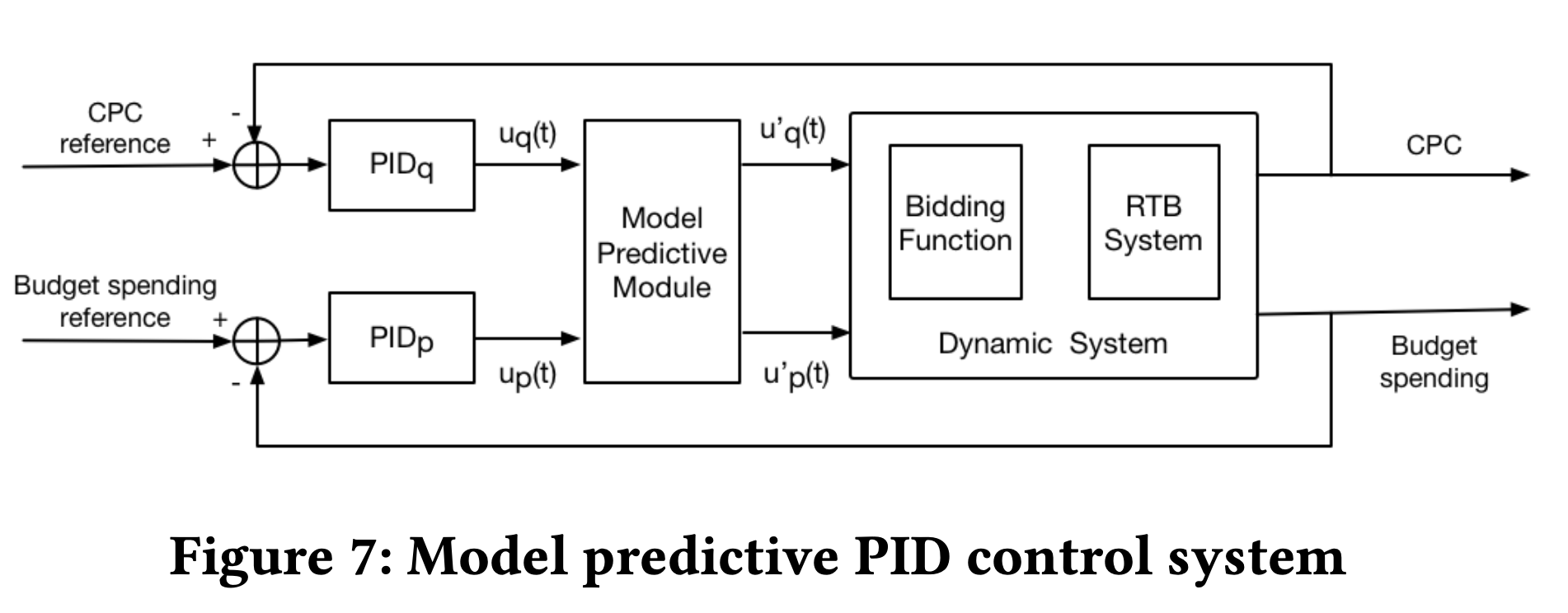
用简单的线性关系去做拟合,并且得到最终的调整系数 \[ \begin{aligned} \begin{bmatrix} \text{Cost}\\ \text{CPC} \end{bmatrix} &= \begin{bmatrix} \bf{X} & \bf{b} \end{bmatrix} \begin{bmatrix} p\\ q\\ 1 \end{bmatrix} \\ \begin{bmatrix} \Delta\text{Cost}\\ \Delta\text{CPC} \end{bmatrix} &= \begin{bmatrix} \bf{X} \end{bmatrix} \begin{bmatrix} \Delta p\\ \Delta q \end{bmatrix} \\ \begin{bmatrix} \Delta p\\ \Delta q \end{bmatrix} &= \begin{bmatrix} \bf{X} \end{bmatrix}^{-1} \begin{bmatrix} \Delta\text{Cost}\\ \Delta\text{CPC} \end{bmatrix} \\ \begin{bmatrix} u'_p(t)\\ u'_q(t) \end{bmatrix} &= \begin{bmatrix} \alpha & 1-\alpha \\ 1 - \beta & \beta \end{bmatrix} \begin{bmatrix} u_p(t)\\ u_q(t) \end{bmatrix} \\ \end{aligned} \]
实验分析
太长先不写。后面如果我自己要做的时候再回来补。
总结
文中关于最优出价的推导还是很精彩的,在满足最优竞得的情况下,从对偶问题出发,得到最优的竞价策略,同时经过分析(其实不用分析,对偶变量就是度量约束松紧的,如果有学运筹的同学,应该能够解读出更多信息)提出用双变量PID的方式来在线调节超参数,做到近似最优求解(目前PID仿佛也是在线背包问题的标准解法了,常用于在线权益方法、流量调控、预算控制等场景),保证出价策略的效率。