Purpose
采样(Sampling)是统计学底下一个比较热门的分支,采样的目的主要有两个:
- 生成服从某个概率分布\(P(x)\) 的样本\(\{x^{(r)}\}^R_{r=1}\)
- 估计某个分布\(P(x)\) 的期望
其中概率分布\(P(x)\) 被称为目标密度(target density),我们假设我们已知分布的概率密度,记为 \[ P(x)=\frac{P^*(x)}{Z} \] 即概率密度函数除以一个归一化常数。有些人会问,既然我们有\(P^*(x)\) ,为什么不能解决采样的问题?这其中存在两个困难,首先是我们并不知道其中的归一化常数 \[ Z=\int P^*(x)d^Nx \] 其次即使我们知道常数\(Z\) ,从\(P(x)\) 中采样得到样本仍然困难,特别是在高维空间中。
Bayesian Sampling
Inverse CDF Sampling
逆累计概率密度(Inverse CDF)是利用cdf来生成样本,生成一个均匀分布的随机数\(u\sim U(0,1)\) ,然后根据概率分布的cdf查找对应的采样值,是最简单的采样方法之一,但我们需要计算概率分布cdf的反函数。
Importance Sampling
重要性采样(Importance Sampling)重点是为了解决估计期望的问题。假设\(Q(x)\) 是一个容易采样的已知分布,对于期望的估计我们有 \[ E(X)=\int xp(x)dx=\int x\frac{p(x)}{q(x)}q(x)dx=\int xw(x)q(x)dx \] 其中\(w(x)=\frac{p(x)}{q(x)}\) ,对于分布\(P(x)\) 的期望我们通常可以这样计算 \[ \hat{E}(X)=\frac{1}{n}\sum_i^n x_i, x\sim P(x) \] 当我们加入分布\(Q(x)\) 时,期望就变成 \[ \hat{E}(X)=\frac{1}{n}\sum^n_ix_i*w(x_i),x_i\sim Q(x) \] 所以,对于易于采样的分布\(Q(x)\) 中采出\(x\) ,对\(x\) 进行加权\(w(x)\) 然后计算期望的估计。
Rejection Sampling
拒绝采样(Rejection Sampling)主要是为了解决第一个问题。我们假设我们找到了一个常数\(c\) 和一个易于计算的提案分布\(Q(x)\) (proposal distribution),使得 \[ \forall x,cQ^*(x)>P^*(x) \] 即如下图所示
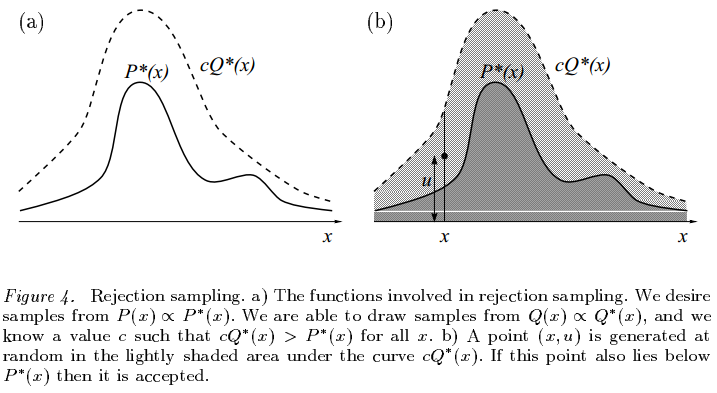
需要采样的时候,我们做两步:
- 在定义域上做均匀分布\(x\sim U(-\infty,+\infty)\) ;
- 做接受概率\(u\sim U(0,cq(x))\) ;
- 如果\(u<\frac{p(x)}{cq(x)}\) ,则接受这个采样的样本\(x\) ,反之则拒绝。
但拒绝采样也会有些许问题,如下图所示,首先我们并不知道常数\(c\) 使得提案分布恒大于目标分布,如果\(c\) 取得小了,则达不到采样的目的,\(c\) 取得大了,采样的效率就会比较低,采样大部分时候都会被拒绝。同时,对于提案分布,当提案分布与目标分布不相似时,采样的效率同样很低。

MCMC
马尔科夫链的蒙特卡洛方法(Markov chain Monte Carlo, MCMC)是一种基于马尔科夫链的蒙特卡洛方法,此篇就不讲解马尔科夫链的相关内容了,MCMC采样的主要思想就是利用马尔科夫的平稳分布来模拟目标分布,随机生成的初始分布并不重要,经过长时间的状态转移之后,初始分布慢慢变成平稳分布,也就是我们的目标分布,而难点就在于怎么构造马尔柯夫的状态转移矩阵。
Metropolis Hastings
Metropolis-Hastings算法的重点在于细致平稳条件的构造 \[ \pi(x)P(x'|x)=\pi(x')P(x|x') \] 状态\(\pi(x)\) 转换到\(\pi(x')\) 的概率和\(\pi(x')\) 转换到\(\pi(x)\) 的概率是相同的,在采样的问题中,也就是采样出\(x_i\) 再采出\(x_j\) 的概率和采样出\(x_j\) 再采出\(x_i\) 的概率相同,可是一般情况下,概率分布会满足细致平稳条件(detailed balance condition) \[ p(x_i)q(x_i,x_j)\neq p(x_j)p(x_j,x_i) \] 所以我们引入一个函数\(\alpha(x,y)\) 使得 \[ p(x_i)q(x_i,x_j)\alpha(x_i,x_j)=p(x_j)p(x_j,x_i)\alpha(x_j,x_i) \] 那么问题来了,这个\(\alpha(x,y)\) 该怎么取?最简单,取对称的函数,即 \[ \alpha(x,y)=p(y)q(y,x) \] 所以我们令 \[ Q'(x_i,x_j)=q(x_i,x_j)\alpha(x_i,x_j) \] 所以以\(Q'(x,y)\) 为转移矩阵,则目标分布\(P(x)\) 就是平稳分布。所以我们做均匀分布的随机数\(u\sim U(0,1)\) ,当\(u<\alpha(x_i,x_j)=p(x_j)q(x_i|x_j)\) ,接收转移,将\(x_j\) 作为采到的样本,重复此步骤,一段时间后,采到的样本就是服从平稳分布的,也就是服从我们的目标分布。
同时,如果\(\alpha(x_i,x_j)\) 过小,则不容易产生新的样本,我们给等号两边同时扩大一定倍数,这样不改变细致平稳条件,也会提高转化概率,所以我们取 \[ \alpha(x_i,x_j)=\min\{\frac{p(x_j)q(x_j,x_i)}{p(x_i)q(x_i,x_j)},1\} \] 注意在不断迭代后,我们只取后部分的样本作为采样得到的样本,因为前面的样本有可能还没有收敛到稳态分布,所以只取后面的样本。
Gibbs Sampling
吉布斯采样(Gibbs Sampling)是Metropolis Hastings的一种变种,当接受概率恒为\(1\) 的时候,同时改用采样于条件分布,Metropolis Hastings就变成了Gibbs Sampling,但适用于多维的分布。对于一组数\(\{x_1,...,x_n\}\) 进行以下迭代 \[ x_1^{t+1}\sim P(x|x_2^t,...,x_n^t) \]
\[ x_2^{t+1}\sim P(x|x_1^{t+1},x_3^t,...,x_n^t) \]
\[ ... \]
\[ x_n^{t+1}\sim P(x|x_1^{t+1},...,x_{n-1}^{t+1}) \]
如此更迭多次之后,得到的样本就是从我们的目标分布中采样得到的分布。
Slice Sampling
切片采样(Slice Sampling)也是一种比较简单的MCMC方法之一,如下图所示
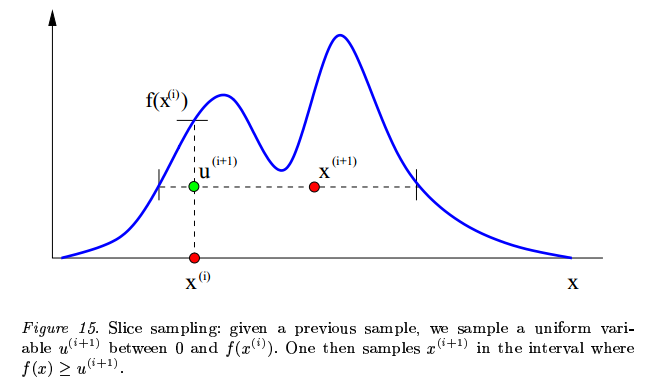
取均匀分布随机数\(x_i\) ,再做均匀分布随机数\(u\sim U(0,f(x_i))\) ,然后再取\(x_{i+1}\) ,如此不断迭代,则可以采样出所需分布的样本。Slice Sampling虽然简单,但是会陷入局部,即某个高峰点,然后难以继续采出下一个点。
Summary
总结了一下常见的采样方法,采样广泛用于图模型和贝叶斯方法,虽然现在传统的统计学习方法和贝叶斯方法现在不如深度学习热门,但这些方法的思想,却值得我们了解,博而广,方才能专而精。