以下内容选自Ensemble Methods Foundations and Algorithms (Zhihua Zhou) 。
A General Boosting Procedure
总的来说Boosting是一种将多个弱分类器(仅比随机猜测好)进行组合,通过对弱分类器的boosted变成强的分类器。一个广义的自助过程(the general boosting procedure)非常简单,可以在任意数据分布上使用,通过不断更正错误来获得新的数据分布,然后训练分类器,最后进行组合的输出。

Adaboost
定义损失函数为指数损失函数 \[ \ell_{\exp}(h|\mathcal{D})=\mathbb{E}_{x\sim\mathcal{D}}[e^{-f(x)h(x)}] \] 其中\(f(x)\) 是真实的标记函数,\(h(x)\) 是弱分类器的预测,弱分类器的加权结合记为 \[ H(x)=\sum^T_{t=1}\alpha_th_t(x) \] 当我们希望整体取得最优时,对损失函数求偏导 \[ \begin {aligned} \frac{\partial e^{-f(x)h(x)}}{\partial H(x)}&=-f(x)e^{-f(x)h(x)}\\ &=-e^{-H(x)}P(f(x)=1|x)+e^{-H(x)}P(f(x)=-1|x)\\ &=0 \end {aligned} \] 得到 \[ H(x)=\frac{1}{2}\ln\frac{P(f(x)=1|x)}{P(f(x)=-1|x)} \] 所以最终的预测结果写作 \[ \begin{aligned} sign(H(x))&=sign(\frac{1}{2}\ln\frac{P(f(x)=1|x)}{P(f(x)=-1|x)})\\ &= \begin{cases} +1,&P(f(x)=1|x)>P(f(x)=-1|x)\\ -1,&P(f(x)=1|x)<P(f(x)=-1|x)\\ \end{cases}\\ &= \underset{y\in\{+1,-1\}}{\arg\min} P(f(x)=y|x) \end{aligned} \] 可见,Adaboost所训练出来的分类器是贝叶斯最优分类器。分类器\(H(x)\) 是由\(h_t\) 和\(\alpha_t\) 迭代生成的,而\(h_t\) 是基于分布\(\mathcal{D}_t\) 生成的,所以我们将指数损失函数写作 \[ \begin{aligned} \ell_{\exp}(\alpha_th_t|\mathcal{D}_t)&=\mathbb{E}_{x\sim\mathbb{D}}[e^{-f(x)\alpha_th_t(x)}]\\ &=\mathbb{E}_{x\sim\mathbb{D}}[e^{-\alpha_t}\mathbb{I}(f(x)=h_t(x))+e^{\alpha_t}\mathbb{I}(f(x)\neq h_t(x))]\\ &=e^{-\alpha_t}P_{x\sim\mathbb{D}}(f(x)=h_t(x))+e^{\alpha_t}P_{x\sim\mathbb{D}}(f(x)\neq h_t(x))\\ &=e^{-\alpha_t}(1-\epsilon_t)+e^{\alpha_t}\epsilon_t \end{aligned} \] 我们对\(\alpha_t\) 求导令其值为\(0\) \[ \frac{\partial \ell_{\exp}(\alpha_th_t|\mathcal{D})}{\partial \alpha_t} =-e^{-\alpha_t}(1-\epsilon_t)+e^{\alpha_t}\epsilon_t=0 \] 得到权重的值应为 \[ \alpha_t=\frac{1}{2}\ln(\frac{1-\epsilon_t}{\epsilon_t}) \] 对于每一步的分类器的损失函数 \[ \begin{aligned} \ell_{\exp}(H_{t-1}+h_t|\mathcal{D})&=\mathbb{E}_{x\sim\mathcal{D}}[e^{-f(x)(H_{t-1}(x)+h_t(x))}]\\ &=\mathbb{E}_{x\sim\mathcal{D}}[e^{-f(x)H_{t-1}(x)}e^{-f(x)h_t(x)}] \end{aligned} \] 我们对其进行泰勒展开 \[ \begin{aligned} \ell_{\exp}(H_{t-1}+h_t|\mathcal{D})&\approx\mathbb{E}_{x\sim\mathcal{D}}[ e^{-f(x)H_{t-1}(x)}(1-f(x)h_t(x)+\frac{f(x)^2h_t(x)^2}{2}) ]\\ &=\mathbb{E}_{x\sim\mathcal{D}}[ e^{-f(x)H_{t-1}(x)}(1-f(x)h_t(x)+\frac{1}{2}) \end{aligned} \] 所以我们第\(t\) 代的分类器应该为 \[ \begin{aligned} h_t(x)&= \underset{h}{\arg\min}\ell_{\exp}(H_{t-1}+h|\mathcal{D})\\ &= \underset{h}{\arg\min}\mathbb{E}_{x\sim\mathcal{D}}[ e^{-f(x)H_{t-1}(x)}(1-f(x)h(x)+\frac{1}{2}) ]\\ &=\underset{h}{\arg\max}\mathbb{E}_{x\sim\mathcal{D}}[ e^{-f(x)H_{t-1}(x)}f(x)h(x) ]\\ &=\underset{h}{\arg\max}\mathbb{E}_{x\sim\mathcal{D}}[ \frac{e^{-f(x)H_{t-1}(x)}}{\mathbb{E}_{x\sim\mathcal{D}}[e^{-f(x)H_{t-1}(x)}]} f(x)h(x) ]\\ \end{aligned} \] 其中\(\mathbb{E}_{x\sim\mathcal{D}}[e^{-f(x)H_{t-1}(x)}]\) 为常数,我们将分布\(\mathcal{D}_t\) 记为 \[ \mathcal{D}_t(x)=\mathcal{D}(x)\frac{e^{-f(x)H_{t-1}(x)}}{\mathbb{E}_{x\sim\mathcal{D}}[e^{-f(x)H_{t-1}(x)}]} \] 所以 \[ \begin{aligned} h_t(x)&=\underset{h}{\arg\max}\mathbb{E}_{x\sim\mathcal{D}}[ \frac{e^{-f(x)H_{t-1}(x)}}{\mathbb{E}_{x\sim\mathcal{D}}[e^{-f(x)H_{t-1}(x)}]} f(x)h(x) ]\\ &=\underset{h}{\arg\max}\mathbb{E}_{x\sim\mathcal{D}_t}[ f(x)h(x) ]\\ \end{aligned} \] 记 \[ f(x)h_t(x)=1-2\mathbb{I}(f(x)\neq h(x)) \] 所以有 \[ h_t(x)=\underset{h}{\arg\min}\mathbb{E}_{x\sim\mathcal{D}_t}[\mathbb{I}(f(x)\neq h(x))] \] 所以每一代选出的弱分类器只跟迭代时的分布有关,而分布的迭代关系如下 \[ \begin{aligned} \mathcal{D}_{t+1}(x)&=\mathcal{D}(x)\frac{e^{-f(x)H_{t}(x)}}{\mathbb{E}_{x\sim\mathcal{D}}[e^{-f(x)H_{t}(x)}]}\\ &=\frac{\mathcal{D}(x)e^{-f(x)H_{t-1}(x)}e^{-f(x)\alpha_th_{t}(x)}}{\mathbb{E}_{x\sim\mathcal{D}}[e^{-f(x)H_{t}(x)}]}\\ &=\mathcal{D}(x)\cdot e^{-f(x)\alpha_th_{t}(x)} \frac{\mathbb{E}_{x\sim\mathcal{D}}[e^{-f(x)H_{t-1}(x)}]}{\mathbb{E}_{x\sim\mathcal{D}}[e^{-f(x)H_{t}(x)}]}\\ \end{aligned} \] 具体算法图下图所示

Theoretical Issues
AdaBoost的upper bound为 \[ \epsilon_{\mathcal{D}}\leq \epsilon_{D}+\tilde{O}(\sqrt{\frac{dT}{m}}) \] 其中\(d\) 是基本的弱分类器的VC维,\(m\) 是训练样本数量,\(T\) 是学习的迭代次数。所以我们易得,为了取得较好的泛化性能,限制基本弱分类器的复杂度和学习迭代的次数同样十分重要。有意思的是,对于AdaBoost这样的算法,即使训练误差接近于0,同样会使训练误差有一定减少
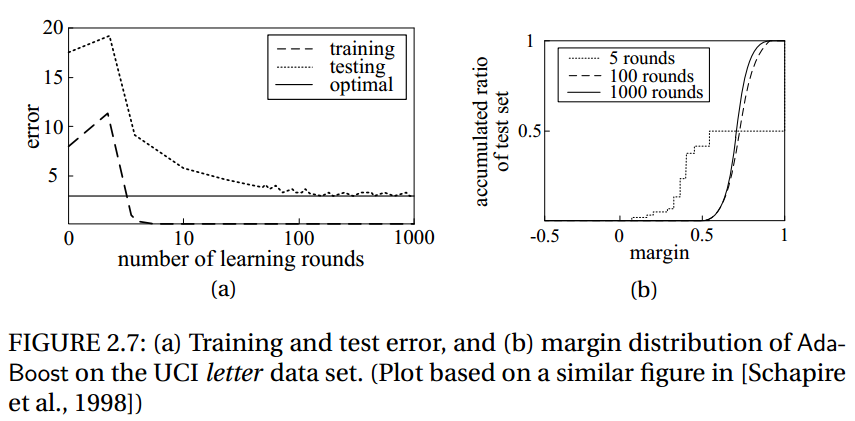
这看似违背了Occam’s Razor原则,即取得相同的效果时我们更偏好简单的模型,所以后人会比较关心为什么AdaBoost算法可以避免过拟合,详情参考ensemble margin等相关理论。
PAC学习理论的学者比较认同Margin理论,但是对于statistic的学者而言,显然这样做并不能让他们满足,他们认为AdaBoost算法可以解释为一种通过不断拟合叠加的对率回归模型的stagewise estimation procedure。

Multiclass Extension
