Benefits of Combination
当我们能够生成一堆基学习器后,与其尝试寻找最好的单个学习器,集成方法通过结合的方式产生更好的泛化性能,其中结合的方式是非常重要的一环。通过结合我们有以下的几个好处
- statistical issue:当我们的假设空间过大,而数据量受限的时候,会有多种不同的假设能够达到相同的准确度,如果学习算法选择了其中之一,就会有一定风险在真实数据上犯错,而通过结合的方式我们就可以尽量规避这种风险;
- computational issue:许多学习算法只是在局部进行搜索最优,即使有充足的训练数据,但是找到最好的假设仍然很困难。通过选择多个不同的起始点来寻找局部最优,结合的方法可以更接近去南局的最优,选择局部最优假设的风险可以被尽量减小;
- representational issue:在多数机器学习任中,当假设空间中不存在真正的标记函数时,通过结合的手段可以尽量去逼近真实标记函数
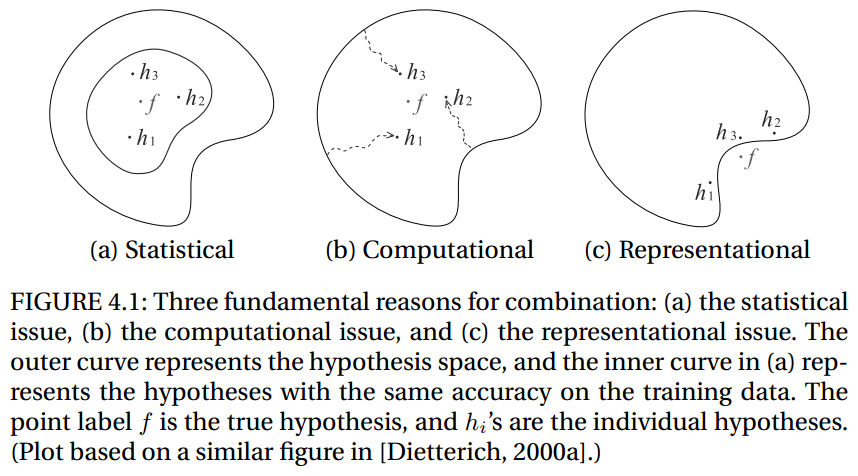
对于statistical issue,我们通常模型具有high variance,对于computational issue则会产生high computational variance,而representational issue会产生high bias。
Averaging
simple averaging
\[ H(x)=\frac{1}{T}\sum^T_{i=1}h_i(x) \]
每一个弱分类器可以写作 \[ h_i(x)=f(x)+\epsilon_i(x),i=1,...,T \] \(h_i(x)\) 的均方误差可以写作 \[ \int (h_i(x)-f(x))^2p(x)dx=\int\epsilon_t(x)^2p(x)dx \] 所以平均误差为 \[ \overline{err}(h)=\frac{1}{T}\sum^T_{i=1}\int\epsilon_t(x)^2p(x)dx \] 结合的学习器的期望误差为 \[ err(H)=\int(\frac{1}{T}\sum^T_{i=1}h_i(x)-f(x))^2p(x)dx =\int(\frac{1}{T}\sum^T_{i=1}\epsilon_i(x))^2p(x)dx \] 所以我们易得 \[ err(H)\leq\overline{err}(h) \] 即集成的误差会小于所有分类器的平均误差。当我们假设误差满足零均值且相互独立时,会有 \[ err(H)=\frac{1}{T}\overline{err}(h) \]
Weighted Averaging
\[ H(x)=\sum^T_{i=1}w_ih_i(x) \]
集成模型的误差为 \[ \begin{aligned} err(H)&=\int (\sum^T_{i=1}w_ih_i(x)-f(x))^2p(x)dx\\ &=\sum^T_{i=1}\sum^T_{j=1}w_iw_jC_{ij} \end{aligned} \] 其中 \[ C_{ij}=\int (h_i(x)-f(x))(h_j(x)-f(x))p(x)dx \] 所以最优的权重为 \[ w=\underset{w}{\arg\min}\sum^T_{i=1}\sum^T_{j=1}w_iw_jC_{ij} \] 求解得 \[ w_i=\frac{\sum^T_{j=1}C_{ij}^{-1}}{\sum^T_{k=1}\sum^T_{j=1}w_iw_jC_{kj}^{-1}} \] 此处注意是用拉格朗日乘子法,以及约束条件是\(\sum w_i=1\) 。虽然权重有解析解,但是实际中,不同基分类器并不会完全不相关,同时协方差矩阵\(C\) 往往是奇异的。
Voting
投票法也是很常用的结合方法,主要有
- Majority Voting 主要投票法
- Plurality Voting 多数投票法
- Weighted Voting 加权投票
- Soft Voting 软投票
Combining by Learning
Stacking
单独的一个学习器被叫做一级学习器(first-level learners),而结合的学习器被称为二级学习器(second-level learner or meta-learner),Stacking就通过多个基学习器联合学习的过程,主要的想法是用原始训练数据去训练一级学习器,然后生成新的学习数据来训练二级学习器,其中第一级学习器的输出作为第二级学习器的输入。

一方面,Stacking可以被看做是一个广义的集成学习方法的框架,另一方面,它也可以看做是特别的结合方式,通过学习来combine。
Other Combination Methods
除此之外,还有一些别的结合方式,此处只列举一二,不详细说明了
- Algebraic Methods
- Behavior Knowledge Space Method
- Decision Template Method