HoORaYs- High-order Optimization of Rating Distance for Recommender System

发表于 | 分类于
今天来看一部南大的发在KDD2017上的推荐系统的论文，HoORaYs。传统的推荐系统，不管是基于显示反馈还是隐式反馈的模型，都是在建立在一阶评分距离原则，而本篇论文是一个高阶评分距离的探索，目标不仅是最小化同个用户同个物品的估计评分与真实评分的距离（也就是一阶评分距离），还最小化同一用户不同物品之间，估计值与评分值之间的差异（二阶评分距离），并将该问题作为一个正则优化问题，并提出了解决算法。 $$ \[\begin{aligned} \min & \sum_{r_{ij}\in R}(r_{ij}-u_i^Tv_j)^2\\ s.t.& \sum_{i=1}^m (u_i)^2 \leq t_u\\ &\sum_{j=1}^n(v_j)^2\leq t_v\\ &\sum_{r_{i,j}}\sum_{r_{i',j'}}I_{iji'j'}(\sigma(u_i^Tv_j,r_{i'j'})-\sigma(r_{ij},r_{i'j'}))=0 \end{aligned}\] \[ 其中$\sigma(x,y)=1/(1+e^{-(x-y)})$ ，当$i'=i\wedge j'\neq j\vee i'\neq i\wedge j'=j$ 时$I_{iji'j'}=1$ （此处我并没有看懂这几个符号是啥意思...Orz，按照之前文章中的意思应该是取同用户不同物品或者同物品不同用户的组合），上式等同于优化： \] {r{ij}}(r_{ij}-u_iTv_j)2+um_{i=1}|u_i|2+v{j=1}n|v_j|2\+d{r{ij}}{r=1}{r_}I_{iji'j'}((u_iTv_j,r{i'j'})-(r_{ij},r_{i'j'}))^2 \[ 因为评分是固定的几个值，如1分到5分，所以我们可以对相同评分的行为进行合并，只计算一次即可，令$|\Omega_{r_{ij},r}|$ 为用户$i$ 给其它物品打$r$ 分或者物品$j$ 收到所有用户对其打$r$ 分的次数，更新方式为 \] \[\begin{aligned} u_i\leftarrow & \lambda_uu_i+(r_{ij}-u_i^Tv_j)v_j\\ & + \lambda_d\sum_{r=1}^{r_\max}|\Omega_{r_{ij},r}|(\sigma(r_{ij},r)\sigma(u_i^Tv_j,r)(1-\sigma(u_i^Tv_j,r))v_j\\ & -\sigma(u_i^Tv_j,r)^2(1-(u_i^Tv_j,r))v_j)\\ v_j\leftarrow & \lambda_vv_j+(r_{ij}-u_i^Tv_j)u_i\\ & + \lambda_d\sum_{r=1}^{r_\max}|\Omega_{r_{ij},r}|(\sigma(r_{ij},r)\sigma(u_i^Tv_j,r)(1-\sigma(u_i^Tv_j,r))u_i\\ & -\sigma(u_i^Tv_j,r)^2(1-(u_i^Tv_j,r))u_i)\\ \end{aligned}\]

$$ 作者还对这一算法进行了几何上的解释

1

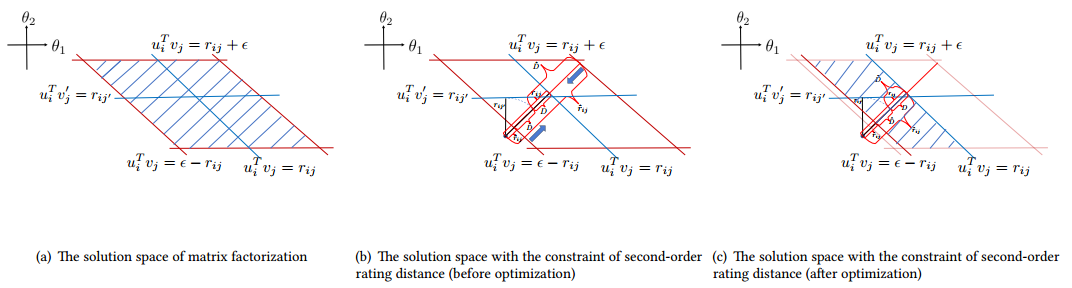
之后还给出了HoORaYs的概率图模型

2
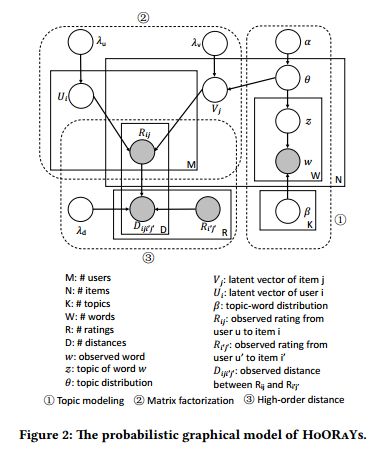
  • 对于每个用户\(i\) ，隐变因子\(u_i\sim\mathcal{N}(0,\lambda_u^{-1}I_K)\)
  • 对于每个物品\(j\) ，
    • topic属性\(\theta_j\sim \text{Dir}(\alpha)\)
    • 物品隐因子\(v_j=\epsilon_j+\theta_j,\epsilon_j\sim\mathcal{N}(0,\lambda_v^{-1}I_K)\)
    • 对于每个词\(w_{jn_w}\)
      • 从topic中指定\(z_{jn_w}\sim \text{Mult}(\theta_j)\)
      • 指定\(w_{jn_w}\sim\text{Mult}(\beta_{z_{jn_w}})\)
  • 对于每个评分项\(r_{ij}\sim\mathcal{N}(u_i^Tv_j,c_{ij}^{-1})\)
  • 对于距离\(d_{iji'j'}\sim\mathcal{N}(\sigma(u_i^Tv_j,r_{i'j'}),\lambda_d^{-1})\)

采用一种EM方式来最大化似然函数求解（具体的木有细看）。

总的来说，这篇文章还是诚意满满，虽然之前这种类似的优化方式也已经有了，比如之前一篇文章中利用item2vec来学习物品相似性来改进物品的隐向量，但这篇文章中作者还是对这种方法做了详细完整的描述，而后面给出了几何角度与概率图模型的分析也很干货满满，思路上还是很精彩的。