这篇文章是Airbnb的一篇文章,发在KDD2017上,介绍了一篇叫梯度提升决策表(Gradient Boosted Decision Tables)的方法。本文的motivation idea有以下几点:
- 可以更好的理解梯度提升bias和variance的权衡,在降低bias的同时,会造成variance的增加,正则化可以在一定程度上解决这些问题,如shrinkage、subsampling等等,传统的限制树模型的复杂度的方式是限制其深度,然而树模型仍然可以自由地划分特征空间,决策表模型可以通过限制切割的位置来控制模型复杂度,在切割位置划分特征空间;
- 对于回归树而言,做梯度提升时通常需要控制每一棵树的复杂度,往往需要在很大的参数空间中去搜索最优解,因此模型选择变得非常“昂贵”,然而由于受限于结构,维数是调整决策表模型的主要参数,因此在梯度提升时,模型选择就变得相对容易;
- 在部署一个集成模型时,往往需要权衡打分效率和模型准确度,决策表模型可以用紧凑的数据结构所表示,大大节约了内存空间,使得我们可以训练更大的模型,同时达到较高的精度,而不用担心打分的延迟。
一个通用的梯度提升框架如下所示:

一个\(d\) 维的决策表用一个\(d\) 维的数组来存储特征下标,另一个\(d\) 维数组来存储划分,一个\(2^d\) 的数组来存储存储预测值(\(d\) 的取值通常较小),预测值通过一个bit的向量来表示,用例子来说明
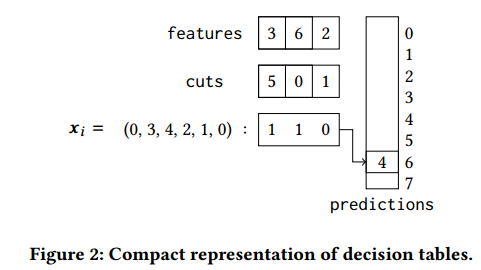
输入\(x_i=(0,3,4,2,1,0)\) ,经过\(d=3\) 个test:\(x_3\leq 5,x_6\leq0,x_2\leq1\)并且产生一个bit向量\([110]_2=[6]_{10}\) ,然后将它的值作为下标值存储。对于每次划分\(k\) ,用\(\mathcal{D}_k\) 表示划分点的子集,\(\mathcal{D}_k^L\) 和\(\mathcal{D}_k^R\) 分别表示划分后的两个集合,大于临界值\(c\) 的和小于等于的,用\(\mathcal{I}_k^L=\{i|x_i\in\mathcal{D}_k^L\}\) 和\(\mathcal{I}_k^R=\{i|x_i\in\mathcal{D}_k^R\}\) 表示划分点的下标,定义均方误差为\(\text{SE}_{\mathcal{D}_k}=\sum_{i\in\mathcal{I}_k}(y_i-\overline{y}_k)^2\) 其中\(\overline{y}_k=\frac{1}{|\mathcal{I}_k|}\sum_{i\in\mathcal{I}_k}y_i\) ,根据基尼系数来划分 \[ \begin{aligned} \text{Gain}(x_j,c)&= \text{SE}_{\mathcal{D}}-\sum_k(\text{SE}_{\mathcal{D}_k^L}+\text{SE}_{\mathcal{D}_k^R})\\ &=\sum_k(\frac{(\sum_{i\in\mathcal{I}_k^L}y_i)^2}{|\mathcal{I}_k^L|}-\frac{(\sum_{i\in\mathcal{I}_k^R}y_i)^2}{|\mathcal{I}_k^R|})-N\overline{y}^2 \end{aligned} \]
\[ \text{Gain}(x_j)=\max_{c\in dom(x_j)}\text{Gain}(x_j,c) \]
很容易看出,寻找最有决策是一个NP问题,所以作者提出了一个反向拟合(backfitting)的方法

首先用贪婪策略去寻找\(d\) 次划分,这样可能不会得到最优解,因此,一旦我们完成\(d\) 次划分的据侧标,用\(n\) 次检验的反向拟合算法来矫正一些次优的划分,每次检验时执行\(d\) 次划分,每次选择\(d\) 次划分之一时来优化划分临界值,并且从当前决策表中去除,计算当前最优化分,更新划分方式。最后,我们计算每次划分的均值来作为预测值。反向拟合主要有以下三种策略:
- 循环反向拟合,cyclic backfitting,从头开始进行划分和优化所有划分序列;
- 随机反向拟合,random backfitting,随机选择一次划分并优化;
- 贪婪反向拟合,gredy backfiting,贪婪策略,选择能最大程度降低variance的划分点。