这次来回顾一下另一个经典模型,Factorization Machine。
Factorization Machine
模型形式如下 \[ \hat{y}(x)=w_0+\sum^n_{i=1}w_ix_i+\sum^n_{i=1}\sum^n_{j=i+1}\langle v_i,v_j\rangle x_ix_j \] 包括对一阶和二阶特征的考虑,这样做是因为我们可以证明对于足够大的\(k\) 存在矩阵\(V\in\mathbb{R}^{n\times k}\) 有 \[ W=VV^T \] 即二阶的权重可以用矩阵分解的形式得到,并且潜在因子的数量决定了二阶权重的质量。这样做有很多好处,首先,在训练集中未出现的权重项就可以通过出现过的权重进行训练,即\(w_{ij}\) 未出现过,但\(v_i\) 和\(v_j\) 却是可以用通过别的项训练出来。同时,可以将计算开销降低至\(O(kn)\) ,证明如下 \[ \begin{aligned} &\sum^n_{i=1}\sum^n_{j=i+1}\langle v_i,v_j\rangle x_ix_j\\ =&\frac{1}{2}\sum^n_{i=1}\sum^n_{j=1}\langle v_i,v_j\rangle x_ix_j-\frac{1}{2}\sum^n_{i=1}\langle v_i,v_i\rangle x_ix_i\\ =&\frac{1}{2}(\sum^n_{i=1}\sum^n_{j=1}\sum^k_{f=1}v_{if}v_{jf}x_ix_j-\sum^n_{i=1}\sum^k_{f=1}v_{if}v_{if}x_ix_i)\\ =&\frac{1}{2}\sum^k_{f=1}(\sum^n_{i=1}\sum^n_{j=1}v_{if}v_{jf}x_ix_j-\sum^n_{i=1}v_{if}v_{if}x_ix_i)\\ =&\frac{1}{2}\sum^k_{f=1}((\sum^n_{i=1}v_{if}x_i)(\sum^n_{j=1}v_{jf}x_j)-\sum^n_{i=1}v_{if}^2x_i^2)\\ =&\frac{1}{2}\sum^k_{f=1}((\sum^n_{i=1}v_{if}x_i)^2-\sum^n_{i=1}(v_{if}x_i)^2)\\ \end{aligned} \] 可以看见里面变成和的平方减去平方的和的形式,大大简化了计算开销,求导更新权重也变得简单 \[ \frac{\partial}{\partial\theta}\hat{y}(x)= \begin{cases} 1&\theta \text{ is }w_0\\ x_i& \theta \text{ is } w_i\\ x_i\sum^n_{j=1}v_{jf}-v_{if}x_i^2&\theta \text{ is } v_{if} \end{cases} \] 同时FM也可以跟SVM一样用kernel的方法进行优化,文章后面作者还跟其他几个常用模型做了比较。
Field-aware Factorization Machines
FFM在FM的基础上提出了域(field)的概念,将不同类别的数据分入不同的field中,然后对每个field的特征作交叉,其实这么做就是为了独立latent factor的影响,论文中给出这样一个例子
| click number | not click number | Publisher | Advertiser |
|---|---|---|---|
| 80 | 20 | ESPN | Nike |
| 10 | 90 | ESPN | Gucci |
| 0 | 1 | ESPN | Adidas |
| 15 | 85 | Vogue | Nike |
| 90 | 10 | Vogue | Gucci |
| 10 | 90 | Vogue | Adidas |
| 85 | 15 | NBC | Nike |
| 0 | 0 | NBC | Gucci |
| 90 | 10 | NBC | Adidas |
预测这样一条数据被点击的概率时
| click | Publisher(P) | Advertiser(A) | Gender(G) |
|---|---|---|---|
| p | ESPN | Nike | Male |
对于FM模型,交叉项为 \[ w_{\text{ESPN}}\cdot w_{\text{Nike}}+w_{\text{ESPN}}\cdot w_{\text{Male}}+w_{\text{Nike}}\cdot w_{\text{Male}} \] 我们可以看出,每个特征的latent factor vector在相互匹配交叉配对的时候都是通用的,即我们训练出Publisher项的\(w_{\text{ESPN}}\) 既可以用在和Advertiser项的交叉中,又可以用在和Gender项的交叉中。而FFM做的就是,Publisher、Advertiser、Gender这三个field彼此两两交叉的时候,不共享同一个latent factor vector,所以就变成这样 \[ w_{\text{ESPN}}^{\text{PA}}\cdot w_{\text{Nike}}^{\text{PA}}+w_{\text{ESPN}}^{\text{PG}}\cdot w_{\text{Male}}^{\text{PG}}+w_{\text{Nike}}^{\text{AG}}\cdot w_{\text{Male}}^{\text{AG}} \] 权重的上标表示权重分解所属于的field,\(w_{\text{ESPN}}^{\text{PA}}\) 仅表示Publisher filed和Advertiser filed的交叉,训练出来的ESPN的latent factor vector。
FM与FFM相比,FM是做所有feature的交叉,所以二次项权重矩阵\(W\in\mathbb{R}^{n\times n}\) 的,其中\(n\) 为特征数,可以视作所有的feature属于一个field,而FFM相当于对\(W\) 的拆分,然后分别训练(自己目前的理解,不一定对,如果不对请各位看官指出) \[ W= \begin{bmatrix} w^{PP}& w^{PA} & w^{PG}\\ w^{AP}& w^{AA}& w^{AG}\\ w^{GP}& w^{GA}& w^{GG} \end{bmatrix} \] 其中每部分都是field交叉特征 \[ w^{PA}= \begin{bmatrix} w_{\text{ESPN,Nike}}&w_{\text{ESPN,Gucci}}&w_{\text{ESPN,Adidas}}\\ w_{\text{Vogue,ESPN}}&w_{\text{Vogue,Gucci}}&w_{\text{Vogue,Adidas}}\\ w_{\text{NBC,Nike}}&w_{\text{NBC,Gucci}}&w_{\text{NBC,Adidas}}\\ \end{bmatrix} \] 其中将\(w^{PA}\) 分解为矩阵相乘形式得到 \[ w_{\text{ESPN,Nike}}=w_{\text{ESPN}}^{\text{PA}}\cdot w_{\text{Nike}}^{\text{PA}} \] 此处等号右边的\(w\) 都是向量,等号左边的\(w\) 为标量,上面写得正式一点应该是 \[ v_{\text{ESPN}}^{\text{PA}}\cdot v_{\text{Nike}}^{\text{PA}}+v_{\text{ESPN}}^{\text{PG}}\cdot v_{\text{Male}}^{\text{PG}}+v_{\text{Nike}}^{\text{AG}}\cdot v_{\text{Male}}^{\text{AG}} =w_{\text{ESPN,Nike}}^{\text{PA}}+w_{\text{ESPN,Male}}^{\text{PG}}+w_{\text{Nike,Male}}^{\text{GA}} \] 讲清楚是什么之后我们再来看怎么算,论文里给出来的是用梯度下降进行迭代计算,计算其中非0值的梯度进行更新。此处我觉得这里依然可以按照FM的方法进行迭代更新,然后每次更新矩阵中的一部分而已。
可是FFM的强大并不在于将latent factor处理为相互的做法,而是提供了一个炒鸡快的多线程实现库libffm。嗯,算得快就是可以这么为所欲为,你快你强大。
Pairwise Interaction Tensor Factorization for Personalized Tag Recommendation
这里补充一下这篇文章,这篇文章是早于FFM提出来的,FFM就是根据这个思想提的,看完FFM再看这篇文章就很清楚了,这篇文章是分了3个field,user、item、tag三个维度做ffm。
Higher-Order Factorization Machines
这篇文章重点在于介绍如何把之前的二阶交叉特征再往高阶去提升,并引入了kernel的方法,引入ANOVA kernel来提升阶数(好像在SVM里见过?),有了高阶特征,如何训练就成了问题,作者在文中给出了多种训练方式,包括梯度下降、坐标上升等等。
Factorization Machines with libFM
这篇文章是对libFM的一个介绍,主要libFM中对于FM的三种计算方法:SGD、ALS和MCMC。其中SGD是原文中最普遍的一种迭代算法,ALS则相对麻烦一点,不断迭代的方式得到收敛解,而MCMC则是求解FM的图模型
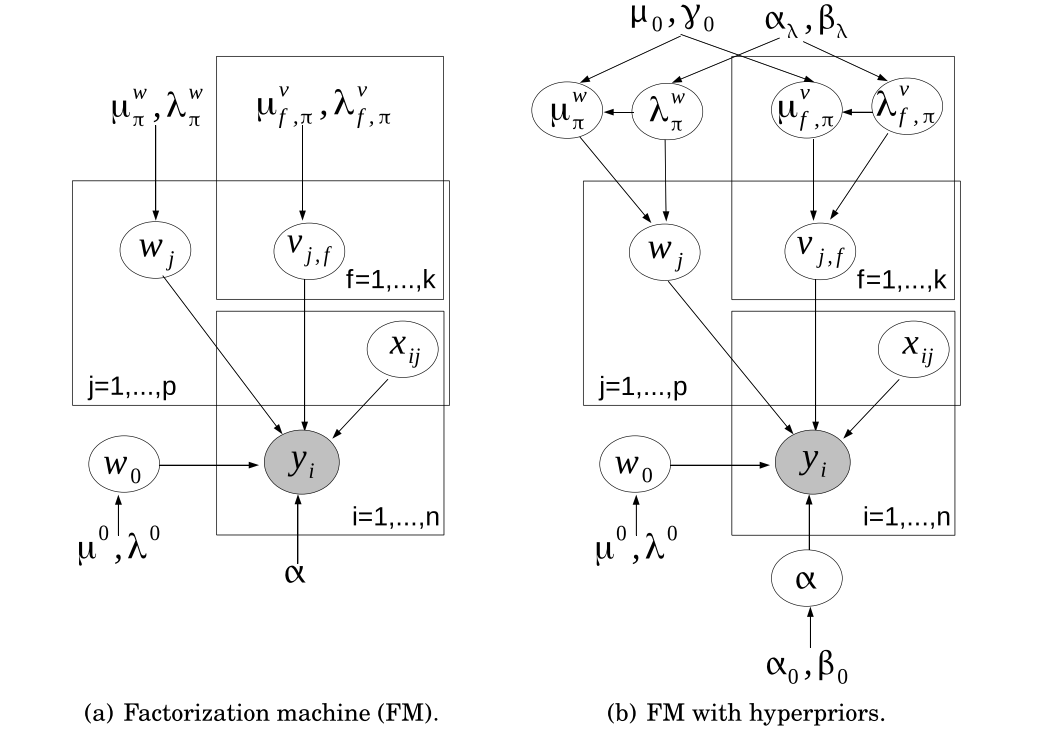
由于我还没怎么入门图模型,就不在这多解释了,不过FM的图模型相对简单很多,看着公式就可以理解。MCMC也在之前博客中讲过了,大家可以去看。
Gradient Boosting Factorization Machines
这篇文章是GBM+FM的组合,说实话前两天我也在想,GBM这么好用,为什么没人把GBM和FM结合或者是MF结合,肯定会有一定提升的,然后今天就读到这篇文章了。这篇文章主要的idea就是对于FFM,并不是所有的field都是有用的feature,所以如选择好的交互特征就需要我们研究,这篇文章就是从这个问题出发的。主要的迭代式为 \[ \hat{y}_s(x)=\hat{y}_{s-1}(x)+\sum_{i\in\mathcal{C}_p}\sum_{j\in\mathcal{C}_q}\mathbb{I}[i,j\in x]\langle V_p^i,V_q^j\rangle \] 其中的\(\mathcal{C}_p\) 和\(\mathcal{C}_q\) 为选取的交叉特征,其中如何选取好的特征则是我们模型的重点,文中采取的算法是选择尽可能使目标函数降低最快的特征,这点跟xgboost就非常相似,有兴趣的各位可以查阅一下(其实基本上完全相同的做法。。。),这里给出算法流程

Neural Factorization Machines for Sparse Predictive Analytics
这篇文章也是融合FM与DL方法的一篇文章,根据FM提出一种神似的叫Bi-Interaction Pooling的结构,用以刻画二阶特征,带入网络计算,网络结构如图所示
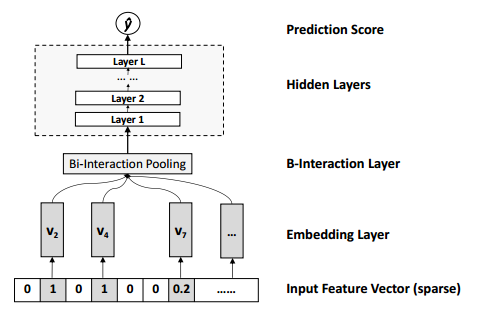
而这个Bi-Interaction Pooling层的计算方式为 \[ f_{\text{BI}}(\mathcal{V}_x)=\sum^n_{i=1}\sum^n_{j=i+1}x_iv_i\odot x_jv_j \] 与FM相似,可以改写为 \[ f_{\text{BI}}(\mathcal{V}_x)=\frac{1}{2}[(\sum^n_{i=1}x_iv_i)^2-\sum^n_{i=1}(x_iv_i)^2] \] 这个想法也还是挺好的,把FM当成pooling层来提取特征,感觉再深入一点应该效果会更好。