Benders Decomposition 总结

这次主要来总结一下这段时间研究的benders算法，主要是在做一个规模不算大的MIP问题，但是公司没有商业求解器用，很蛋疼。我主要参考一篇17年的综述文章[1]，翻译为主，而且仅写了最近浏览过和比较感兴趣的部分，并不全面，同时会写点自己的理解，但还是希望大家能去看一下原文。同时这次也是参考了QinHu老师之前的内容，在这放出链接，感觉他们写得比我的全面且详细：

Benders教学1

Benders教学2

Benders Decomposition简介

Benders Decompostion（BD）最早在[2]于1962年提出，是一种非常流行的解决含有复杂变量（当该变量固定后，原问题会变成一个易于求解）的问题，并且在很多小方向上都有广泛应用，如调度、运输等等。BD是基于一系列投影映射和松弛，原问题最先被影射到由复杂变量定义的子空间，然后再做对偶，通过极射线和极点来定义可行割（feasibility cut）和最优割（optimality cuts）来约束复杂变量，也就是枚举所有的极射线和极点。但枚举往往是不可行的，所以我们可以对可行割和最优割采用一种松弛的策略，建立主问题（Master Problem）和子问题（Subproblem），通过迭代求解的方式，来确定搜索的顺序，产生有效的割。跟B&B一样，也是一种“聪明”的“枚举”。

BD最早被应用在MIP问题上，其中固定了“复杂”的整数变量，原问题就成为一个LP问题，可以快速求解。考虑经典的MIP问题： \[ \begin{aligned} \min && f^Ty+c^Tx\\ \text{s.t.} && Ay=b\\ && By+Dx=d\\ && x \in \mathbb{R}_+^{n_2} \quad y \in \mathbb{Z}_+^{n_1}\\ \end{aligned} \] 上述模型可以简写为 \[ \min_{\bar{y}\in Y} \lbrace f^T\bar{y}+ \min_{x\geq0} \{c^Tx:Dx=d-B\bar{y} \} \rbrace \] 其中\(\bar{y}\)是给定值的复杂变量。内部是求最小的一个LP问题，令\(\pi\)为其约束\(Dx=d-B\bar{y}\)所对应的对偶变量，则有

\[ \max_{\pi\in\mathbb{R}^{m_2}_+}\{\pi^T(d-B\bar{y}):\pi^T D\leq c\} \]

根据对偶理论，我们有

\[ \min_{\bar{y}\in Y} \lbrace f^T\bar{y}+ \max_{\pi\in\mathbb{R}^{m_2}} \{\pi^T(d-B\bar{y}):\pi^TD\leq c\} \rbrace \]

内部的最大化问题的可行域\(F=\{\pi|\pi^TD\leq c\}\)是独立于\(\bar{y}\)的，因此，对于任意给定的\(\bar{y}\)，如果\(F\)非空，里面的最大化的问题要么是无界的，要么是可行的。对于前一种情况，极射线\(Q\)的集合，\(Q\subset F\)，定义了一个无界的方向\(r_q,q\in Q,r_q^T(d-B\bar{y})>0\)。为了避免这种情况（因为对偶出现无界解，原问题无最优解），所以我们需要避免这种情况的发生，在原问题中加割（cut） \[ r_q^T(d-B\bar{y})\leq 0\quad \forall q\in Q \] 对于后一种情况，内部最大化问题的解是一个极点\(\pi_e,e\in E\)，其中\(E\)是可行域\(F\)中极点的集合，所以原问题等价于 \[ \begin{aligned} \min_{\bar{y}\in Y} && f^T\bar{y} + \max_{e\in E}\{\pi_e^T(d-B\bar{y})\}\\ \text{s.t.} && r_q^T(d-B\bar{y})\leq 0\quad \forall q\in Q \end{aligned} \] 我们用变量\(\eta\in\mathbb{R}^1_+\)来获得其等价问题，定义主问题（MP）为 \[ \begin{aligned} \min_{y,\eta} && f^Ty + \eta \\ \text{s.t.} && Ay=b\\ && \eta \geq \pi_e^T(d-By) && e \in E\\ && 0 \geq \pi_q^T(d-By) && q \in Q\\ && y \geq 0 \quad \text{and integer} \end{aligned} \] 其中第二个和第三个约束被称为最优割和可行割。如果想完整枚举出所有的割是不现实的，所以[2]中提出了一种迭代的方式来产生割，BD重复求解MP问题，每次求解时候只加入可行割和最优割的一部分子集（初始的时候可以为空集），然后给定复杂变量\(\bar{y}\)通过求解子问题，逐步加入可行割或者最优割。通过迭代不断产生新的割，MP则会收敛至最优解，MP的目标函数值为原问题提供了一个有效的下界，而子问题对偶为原问题提供了一个有效的上界。

Benders Dcomposition实现

之前网上秦老师有一版java调用cplex的实现，但。。我java水平真一般。。看得很费劲，加上这次做项目，就同样的例子自己用python调用gurobi和谷歌的or-tools自己实现了一遍。用or-tools主要是因为公司目前还没有买开源求解器，目前还在用cbc，而or-tools提供了统一的接口封装，相对友好（但实现的功能也少了很多）。

还有，因为or-tools上暂时没找到cbc的相关api，所以基于or-tools里面只实现combinatorial benders cuts。

Gurobi实现

import numpy as np
from gurobipy import *

example = 1
cuts_type = "general"
# cuts_type = "cb"

if example == 1:
    # example 1, optimal 350
    num_s = 4
    num_d = 3
    supply = [10, 30, 40, 20]
    demand = [20, 50, 30]
    c = np.array([
        [2, 3, 4],
        [3, 2, 1],
        [1, 4, 3],
        [4, 5, 2]
    ])
    f = np.array(
        [[10, 30, 20] for _ in range(4)]
    )
    bar_y = np.array([
        [0, 1, 0],
        [0, 0, 1],
        [1, 1, 0],
        [0, 1, 0]
    ])
elif example == 2:
    # example 2, optimal 4541
    num_s = 8
    num_d = 7
    supply = [20, 20, 20, 18, 18, 17, 17, 10]
    demand = [20, 19, 19, 18, 17, 16, 16]
    c = np.array([
        [31, 27, 28, 10, 7, 26, 30],
        [15, 19, 17, 7, 22, 17, 16],
        [21, 17, 19, 29, 27, 22, 13],
        [9, 19, 7, 15, 20, 17, 22],
        [19, 7, 18, 10, 12, 27, 23],
        [8, 16, 10, 10, 11, 13, 15],
        [14, 32, 22, 10, 22, 15, 19],
        [30, 27, 24, 26, 25, 15, 19]
    ]).reshape(num_s, num_d)
    f = np.array([
        [649, 685, 538, 791, 613, 205, 467],
        [798, 211, 701, 506, 431, 907, 945],
        [687, 261, 444, 264, 443, 946, 372],
        [335, 385, 967, 263, 423, 592, 939],
        [819, 340, 233, 889, 211, 854, 823],
        [307, 620, 845, 919, 223, 854, 823],
        [560, 959, 782, 417, 358, 589, 383],
        [375, 791, 720, 416, 251, 887, 235]
    ])
    bar_y = np.array([
        [0, 1, 0, 0, 0, 0, 1],
        [0, 0, 1, 0, 0, 0, 0],
        [1, 1, 0, 1, 0, 0, 0],
        [0, 1, 0, 1, 1, 0, 0],
        [0, 0, 0, 0, 0, 1, 0],
        [1, 0, 1, 0, 1, 0, 1],
        [0, 1, 0, 1, 0, 1, 0],
        [0, 0, 0, 1, 1, 1, 0]
    ])
else:
    print("Example not found")

M = np.ones((num_s, num_d))
for i in range(num_s):
    for j in range(num_d):
        M[i, j] = min(supply[i], demand[j])

params = dict()
params["num_s"] = num_s
params["num_d"] = num_d
params["supply"] = supply
params["demand"] = demand
params["c"] = c
params["f"] = f
params["M"] = M

"""
# ====================== solve problem directly ====================== 
mip = Model()
x = mip.addVars([i for i in range(num_s)], [j for j in range(num_d)], vtype=GRB.CONTINUOUS, name="x")
y = mip.addVars([i for i in range(num_s)], [j for j in range(num_d)], vtype=GRB.BINARY, name="y")
mip.setObjective(
    quicksum(
        quicksum(
            x[i,j] * c[i,j] + y[i,j] * f[i,j]
            for j in range(num_d)
        )
        for i in range(num_s)
    ), GRB.MINIMIZE
)
u = mip.addConstrs((
    quicksum(
        x[i,j] for j in range(num_d)
    ) <= supply[i]
    for i in range(num_s) 
))
v = mip.addConstrs((
    quicksum(
        x[i,j] for i in range(num_s)
    ) >= demand[j]
    for j in range(num_d)
))
w = mip.addConstrs((
    x[i,j] <= M[i,j] * y[i,j]
    for i in range(num_s)
    for j in range(num_d)
))

mip.optimize()
"""

# ====================== benders decomposition ======================
def mp(Q, E, iter_i, parameter, cuts_type):
    # read parameters
    num_s = parameter["num_s"]
    num_d = parameter["num_d"]
    supply = parameter["supply"]
    demand = parameter["demand"]
    c = parameter["c"]
    f = parameter["f"]
    stop = False

    # master problem
    print("=" * 20 + " master problem " + "=" * 20)
    master = Model("master")

    y = master.addVars(
        [i for i in range(num_s)],
        [j for j in range(num_d)],
        vtype=GRB.BINARY, name="y"
    )

    q = master.addVar(vtype=GRB.CONTINUOUS, name="q")

    master.addConstrs((
        quicksum(y[i,j] for i in range(num_s)) >= 1
        for j in range(num_d)
    ))

    master.addConstrs((
        quicksum(y[i,j] for j in range(num_d)) >= 1
        for i in range(num_s)
    ))

    if cuts_type == "general":
        # benders feasiblity cut
        for item in Q.values():
            master.addConstr(
                quicksum(-1 * supply[i] * item["u"][i] for i in range(num_s)) +
                quicksum(demand[j] * item["v"][j] for j in range(num_d)) +
                quicksum(-1 * M[i, j] * item["w"][i, j] * y[i, j] 
                         for i in  range(num_s) 
                         for j in range(num_d)
                ) <= 0
            )
    elif cuts_type == "cb":
        # addConstraints do not support dict enumeration
        # combinatorial benders cut
        for item in Q.values():
            master.addConstr(
                quicksum(y[i, j] for (i, j) in item[0]) +
                quicksum(1 - y[i, j] for (i, j) in item[1]) >= 1
            )
    else:
        print("no available cuts types")

    # benders optimality cut
    for item in E.values():
        master.addConstr(
            quicksum(-1 * supply[i] * item["u"][i] for i in range(num_s)) +
            quicksum(demand[j] * item["v"][j] for j in range(num_d)) +
            quicksum(-1 * M[i, j] * item["w"][i, j] * y[i, j] for i in range(num_s) for j in range(num_d))
            <= q
        )

    master.setObjective(quicksum(
        f[i, j] * y[i, j]
        for i in range(num_s)
        for j in range(num_d)
    ) + q, GRB.MINIMIZE)

    master.optimize()
    bar_y = dict()
    if master.status == GRB.OPTIMAL:
        for i in range(num_s):
            for j in range(num_d):
                bar_y[i, j] = 1 if y[i, j].x > 0.01 else 0
    else:
        print("There is no feasible solution in primal problem")
        stop = True

    return master, bar_y, stop


def sp(Q, E, bar_y, iter_i, parameter):
    # read parameters
    num_s = parameter["num_s"]
    num_d = parameter["num_d"]
    supply = parameter["supply"]
    demand = parameter["demand"]
    c = parameter["c"]
    f = parameter["f"]
    M = parameter["M"]
    stop = False

    # dual problem of slave problem
    print("=" * 20 + " slave problem with general feasible cuts " + "=" * 20)
    dual = Model("dual_slave")

    # get unboundedRay
    dual.Params.InfUnbdInfo = 1

    u = dual.addVars([i for i in range(num_s)], name="u")
    v = dual.addVars([j for j in range(num_d)], name="v")
    w = dual.addVars([i for i in range(num_s)], [j for j in range(num_d)], name="w")

    dual.setObjective(
        quicksum(-1 * supply[i] * u[i] for i in range(num_s)) +
        quicksum(demand[j] * v[j] for j in range(num_d)) +
        quicksum(
            -1 * M[i,j] * bar_y[i,j] * w[i,j]
            for i in range(num_s)
            for j in range(num_d)
        ), GRB.MAXIMIZE
    ) 

    dual.addConstrs((
        -1 * u[i] + v[j] - w[i,j] <= c[i,j]
        for i in range(num_s)
        for j in range(num_d)
    ))

    dual.optimize()

    if dual.status == GRB.UNBOUNDED:
        item = dict()
        item["u"] = {i:u[i].unbdRay for i in range(num_s)}
        item["v"] = {j:v[j].unbdRay for j in range(num_d)}
        item["w"] = {(i,j):w[i,j].unbdRay for i in range(num_s) for j in range(num_d)}
        Q[iter_i] = item
        print("Add feasible cut")
    elif dual.status == GRB.OPTIMAL:
        item = dict()
        item["u"] = {i:u[i].x for i in range(num_s)}
        item["v"] = {j:v[j].x for j in range(num_d)}
        item["w"] = {(i,j):w[i,j].x for i in range(num_s) for j in range(num_d)}
        E[iter_i] = item
        print("Add optimal cut")
    else:
        print("wrong slave sub-problem status  " + str(dual.status))
        stop = True

    return dual, stop


def sp_cb(Q, E, bar_y, iter_i, parameter):
    # read parameters
    num_s = parameter["num_s"]
    num_d = parameter["num_d"]
    supply = parameter["supply"]
    demand = parameter["demand"]
    c = parameter["c"]
    f = parameter["f"]
    M = parameter["M"]
    stop = False

    # slave problem
    print("=" * 20 + " slave problem with cb feasible cuts " + "=" * 20)
    slave = Model("slave")

    x = slave.addVars(
        [i for i in range(num_s)],
        [j for j in range(num_d)],
        vytpe=GRB.CONTINUOUS, name="x"
    )

    con_u = slave.addConstrs((
        quicksum(
            -1 * x[i, j] for j in range(num_d)
        ) >= -1 * supply[i]
        for i in range(num_s)
    ))

    con_v = slave.addConstrs((
        quicksum(
            x[i, j] for i in range(num_s)
        ) >= demand[j]
        for j in range(num_d)
    ))

    con_w = slave.addConstrs((
        -1 * x[i, j] + bar_y[i, j] * M[i, j] >= 0
        for i in range(num_s)
        for j in range(num_d)
    ))

    slave.setObjective(quicksum(
        c[i, j] * x[i, j]
        for i in range(num_s)
        for j in range(num_d)
    ), GRB.MINIMIZE)

    slave.optimize()

    if slave.status == GRB.INFEASIBLE:
        item = dict()
        item[0] = [
            k for k, v in bar_y.items() if v < 0.001
        ]
        item[1] = [
            k for k, v in bar_y.items() if v >= 0.001
        ]
        Q[iter_i] = item
        print("Add feasible cut")
    elif slave.status == GRB.OPTIMAL:
        item = dict()
        item["u"] = {k: v.pi for k, v in con_u.items()}
        item["v"] = {k: v.pi for k, v in con_v.items()}
        item["w"] = {k: v.pi for k, v in con_w.items()}
        E[iter_i] = item
        print("Add optimal cut")
    else:
        print("wrong slave sub-problem status  " + str(slave_status))
        stop = True

    return slave, stop


# main iteration
E_set = dict()
Q_set = dict()

LB = -1 * 1e10
UB = 1e10

warm_start = True
feasible_cnt = 0
optimal_cnt = 0

for iter_i in range(1000):

    if np.abs(UB - LB) < 0.01:
        print("Optimal")
        break

    print("=" * 100)
    print("iteration at " + str(iter_i))

    if cuts_type == "general":
        dual, stop = sp(Q_set, E_set, bar_y, iter_i, params)
        
    elif cuts_type == "cb":
        slave, stop = sp_cb(Q_set, E_set, bar_y, iter_i, params)

    else:
        print("no available cuts type")
        break

    print("Q  " + str(len(Q_set.keys())))
    print("E  " + str(len(E_set.keys())))

    if stop:
        print("Wong slave problem")
        break

    item = E_set.get(iter_i, False)
    if item:

        dual_optimal = sum(
            [-1 * supply[i] * item["u"][i] for i in range(num_s)]
        ) + sum(
            [demand[j] * item["v"][j] for j in range(num_d)]
        ) + sum(
            [-1 * M[i, j] * bar_y[i, j] * item["w"][i, j]
            for i in range(num_s)
            for j in range(num_d)]
        )

        print("slave dual objective value")
        print(dual_optimal)

        UB = min(
            UB, dual_optimal + sum(
                [bar_y[i, j] * f[i, j]
                for i in range(num_s)
                for j in range(num_d)]
            )
        )
    
    master, bar_y, stop = mp(Q_set, E_set, iter_i, params, cuts_type)

    print("bar_y")
    print(bar_y)

    print("master objective value")
    print(master.objVal)

    if stop:
        print("wrong master problem")
        break

    LB = master.objVal

    print("UB " + str(UB))
    print("LB " + str(LB))

Or-tools(CBC)实现

import numpy as np
from collections import defaultdict
from ortools.linear_solver import pywraplp

example = 1

if example == 1:
    # example 1, optimal 350
    num_s = 4
    num_d = 3
    supply = [10, 30, 40, 20]
    demand = [20, 50, 30]
    c = np.array([
        [2, 3, 4],
        [3, 2, 1],
        [1, 4, 3],
        [4, 5, 2]
    ])
    f = np.array(
        [[10, 30, 20] for _ in range(4)]
    )
    bar_y = np.array([
        [0, 1, 0],
        [0, 0, 1],
        [1, 1, 0],
        [0, 1, 0]
    ])
elif example == 2:
    # example 2, optimal 4541
    num_s = 8
    num_d = 7
    supply = [20, 20, 20, 18, 18, 17, 17, 10]
    demand = [20, 19, 19, 18, 17, 16, 16]
    c = np.array([
        [31, 27, 28, 10, 7, 26, 30],
        [15, 19, 17, 7, 22, 17, 16],
        [21, 17, 19, 29, 27, 22, 13],
        [9, 19, 7, 15, 20, 17, 22],
        [19, 7, 18, 10, 12, 27, 23],
        [8, 16, 10, 10, 11, 13, 15],
        [14, 32, 22, 10, 22, 15, 19],
        [30, 27, 24, 26, 25, 15, 19]
    ])
    f = np.array([
        [649, 685, 538, 791, 613, 205, 467],
        [798, 211, 701, 506, 431, 907, 945],
        [687, 261, 444, 264, 443, 946, 372],
        [335, 385, 967, 263, 423, 592, 939],
        [819, 340, 233, 889, 211, 854, 823],
        [307, 620, 845, 919, 223, 854, 823],
        [560, 959, 782, 417, 358, 589, 383],
        [375, 791, 720, 416, 251, 887, 235]
    ])
    bar_y = np.array([
        [0, 1, 0, 0, 0, 0, 1],
        [0, 0, 1, 0, 0, 0, 0],
        [1, 1, 0, 1, 0, 0, 0],
        [0, 1, 0, 1, 1, 0, 0],
        [0, 0, 0, 0, 0, 1, 0],
        [1, 0, 1, 0, 1, 0, 1],
        [0, 1, 0, 1, 0, 1, 0],
        [0, 0, 0, 1, 1, 1, 0]
    ])
else:
    print("Example not found")

M = np.ones((num_s, num_d))
for i in range(num_s):
    for j in range(num_d):
        M[i, j] = min(supply[i], demand[j])

params = dict()
params["num_s"] = num_s
params["num_d"] = num_d
params["supply"] = supply
params["demand"] = demand
params["c"] = c
params["f"] = f
params["M"] = M

'''
# ====================== solve problem directly ======================
# init solver
solver = pywraplp.Solver("test", pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)
# solver = pywraplp.Solver("test", pywraplp.Solver.GLOP_LINEAR_PROGRAMMING)
# solver = pywraplp.Solver("test", pywraplp.Solver.CLP_LINEAR_PROGRAMMING)

# add variables
x = dict()
y = dict()
for i in range(num_s):
    for j in range(num_d):
        x[i, j] = solver.NumVar(0, solver.infinity(), 'x[%i,%i]' % (i, j))
        y[i, j] = solver.IntVar(0, 1, 'y[%i,%i]' % (i, j))

    # add objective
z = solver.Sum([
    solver.Sum([
        c[i, j] * x[i, j] + f[i, j] * y[i, j]
        for i in range(num_s)
    ]) for j in range(num_d)
])
objective = solver.Minimize(z)

# add constraints
st_s = dict()
for i in range(num_s):
    st_s[i] = solver.Add(solver.Sum([x[i, j] for j in range(num_d)]) <= supply[i])
st_d = dict()
for j in range(num_d):
    st_d[i] = solver.Add(solver.Sum([x[i, j] for i in range(num_s)]) >= demand[j])
st_f = dict()
for i in range(num_s):
    for j in range(num_d):
        st_f[i, j] = solver.Add(x[i, j] <= M[i, j] * y[i, j])

# optimize
solver.Solve()

print('z = ', solver.Objective().Value())
for i in range(num_s):
    for j in range(num_d):
        print("x%i%i  " % (i, j) + str(x[i, j].solution_value()))
        print("y%i%i  " % (i, j) + str(y[i, j].solution_value()))

'''


# ====================== benders decomposition ======================


def mp(Q, E, iter_i, parameter):
    # read parameters
    num_s = parameter["num_s"]
    num_d = parameter["num_d"]
    supply = parameter["supply"]
    demand = parameter["demand"]
    c = parameter["c"]
    f = parameter["f"]
    stop = False

    # master problem
    print(" === master problem ===")
    master = pywraplp.Solver("master%i" % iter_i, pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)

    y = dict()
    for i in range(num_s):
        for j in range(num_d):
            y[i, j] = master.IntVar(0, 1, "y[%i,%i]" % (i, j))

    q = master.NumVar(0, master.infinity(), "q")

    # other constraints
    for i in range(num_s):
        master.Add(master.Sum([y[i, j] for j in range(num_d)]) >= 1)
    for j in range(num_d):
        master.Add(master.Sum([y[i, j] for i in range(num_s)]) >= 1)

    # general benders optimality cut
    for item in E.values():
        master.Add(
            master.Sum([-1 * supply[i] * item["u"][i] for i in range(num_s)]) +
            master.Sum([demand[j] * item["v"][j] for j in range(num_d)]) +
            master.Sum([
                -1 * M[i, j] * item["w"][i, j] * y[i, j]
                for i in range(num_s)
                for j in range(num_d)
            ]) <= q
        )

    # general benders feasiblity cuts
    # add extreme ray
    # or-tools does not support getRay() 
    # combinatorial benders cuts
    for item in Q.values():
        master.Add(
            master.Sum([y[i, j] for (i, j) in item[0]]) +
            master.Sum([1 - y[i, j] for (i, j) in item[1]])
            >= 1
        )

    master.Minimize(master.Sum([
        f[i, j] * y[i, j]
        for i in range(num_s)
        for j in range(num_d)
    ]) + q)

    master_status = master.Solve()

    # if optimal or feasible
    bar_y = dict()
    if master_status == 0:
        for i in range(num_s):
            for j in range(num_d):
                bar_y[i, j] = 1 if y[i, j].solution_value() > 0.1 else 0
    else:
        print("There is no feasible solution in primal problem")
        stop = True

    return master, bar_y, stop


def sp(Q, E, bar_y, iter_i, parameter):
    # read parameters
    num_s = parameter["num_s"]
    num_d = parameter["num_d"]
    supply = parameter["supply"]
    demand = parameter["demand"]
    c = parameter["c"]
    f = parameter["f"]
    M = parameter["M"]
    stop = False

    # slave sub-problem
    print(" === slave sub-problem ===")
    slave = pywraplp.Solver("slave%i" % iter_i, pywraplp.Solver.CLP_LINEAR_PROGRAMMING)

    x = dict()
    for i in range(num_s):
        for j in range(num_d):
            x[i, j] = slave.NumVar(0, M[i, j], "x[%i,%i]" % (i, j))

    con_u = dict()
    for i in range(num_s):
        con_u[i] = slave.Add(slave.Sum([
            -1 * x[i, j] for j in range(num_d)
        ]) >= -1 * supply[i])

    con_v = dict()
    for j in range(num_d):
        con_v[j] = slave.Add(slave.Sum([
            x[i, j] for i in range(num_s)
        ]) >= demand[j])

    con_w = dict()
    for i in range(num_s):
        for j in range(num_d):
            con_w[i, j] = slave.Add(
                -1 * x[i, j] + M[i, j] * bar_y[i, j] >= 0
            )

    slave.Minimize(slave.Sum([
        c[i, j] * x[i, j]
        for i in range(num_s)
        for j in range(num_d)
    ]))

    slave_status = slave.Solve()

    if slave_status == slave.OPTIMAL:
        item = dict()
        item["u"] = {k: u.dual_value() for k, u in con_u.items()}
        item["v"] = {k: v.dual_value() for k, v in con_v.items()}
        item["w"] = {k: w.dual_value() for k, w in con_w.items()}
        E[iter_i] = item
    elif slave_status == slave.INFEASIBLE:
        # general benders feasiblity cuts should have been added
        # or-tools does not support getRay() which exists in cplex
        # so we add combinatorial cuts instead

        # combinatorial benders cuts
        item = defaultdict(list)
        for i in range(num_s):
            for j in range(num_d):
                if bar_y[i, j] > 0:
                    item[1].append((i, j))
                else:
                    item[0].append((i, j))
        Q[iter_i] = item
    else:
        print("wrong slave sub-problem status  " + str(slave_status))
        stop = True

    return slave, stop


# main iteration
Q_set = dict()
E_set = dict()

LB = -1 * 1e10
UB = 1e10

for iter_i in range(1000):

    if np.abs(UB - LB) < 0.01:
        print("Optimal")
        # break

    print("=" * 100)
    print("iteration at " + str(iter_i))

    slave, stop = sp(Q_set, E_set, bar_y, iter_i, params)

    print("Q  " + str(len(Q_set.keys())))
    print("E  " + str(len(E_set.keys())))

    if stop:
        print("Wong slave problem")
        break

    item = E_set.get(iter_i, False)
    if item:
        print("slave objective value")
        print(slave.Objective().Value())

        dual_optimal = sum(
            [-1 * supply[i] * item["u"][i] for i in range(num_s)]
        ) + sum(
            [demand[j] * item["v"][j] for j in range(num_d)]
        ) + sum(
            [-1 * M[i, j] * bar_y[i, j] * item["w"][i, j]
             for i in range(num_s)
             for j in range(num_d)]
        )

        print("slave dual objective value")
        print(dual_optimal)

        UB = min(
            UB, dual_optimal + sum(
                [bar_y[i, j] * f[i, j]
                 for i in range(num_s)
                 for j in range(num_d)]
            )
        )

    master, bar_y, stop = mp(Q_set, E_set, iter_i, params)

    print("bar_y")
    print(bar_y)

    print("master objective value")
    print(master.Objective().Value())

    if stop:
        print("wrong master problem")
        break

    LB = master.Objective().Value()

    print("UB " + str(UB))
    print("LB " + str(LB))

Benders Decomposition 改进优化

MP虽然提供了一个很好的求解MIP甚至是MNLP问题的框架，但也同时有很多问题：时间很长的迭代过程，产生的割有可能很弱，特殊情况收敛慢等等。很多文献都做了BD的优化，一方面是通过减少迭代的次数来改进算法的收敛性，另一方面是减少每次迭代的耗时，前者是通过改善产生解和割的质量，后者则是通过改善产生解的过程和每步求解主问题子问题的方式。

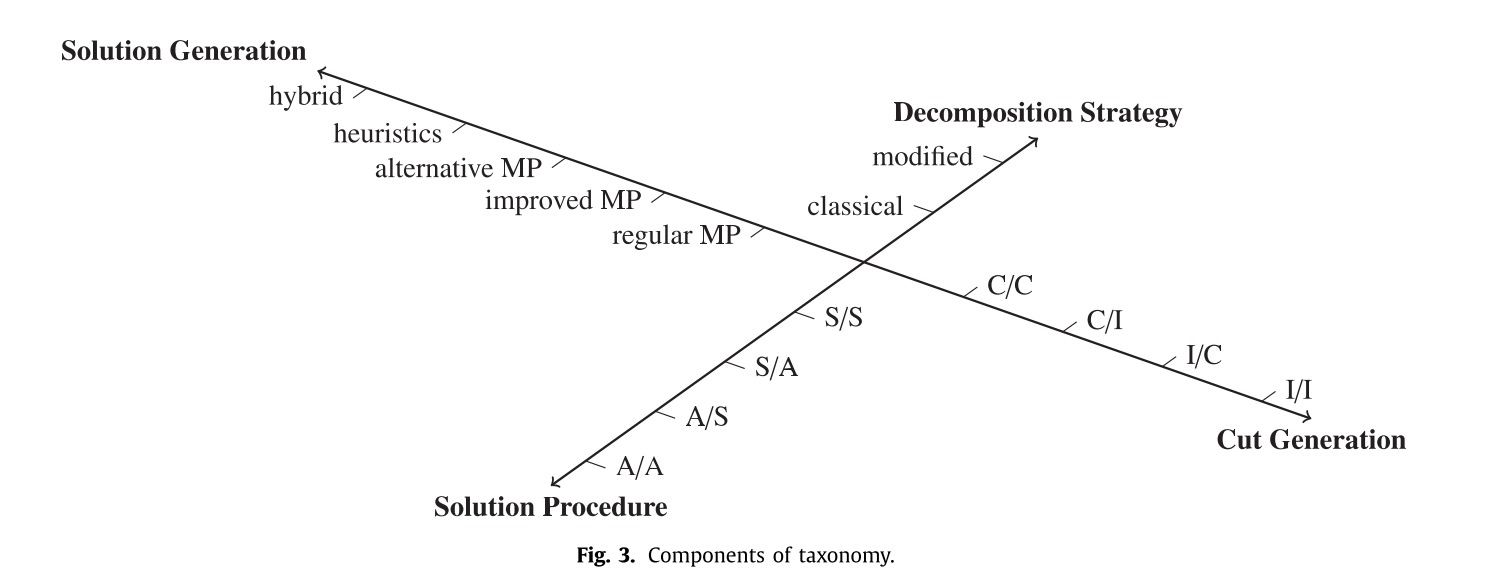
主要通过四个方向来改进BD：

主问题和子问题分解策略
主问题和子问题求解的过程，图中“S”之标准求解过程，“A”指特别的求解方式，“S/A”指标准的方式求解主问题，特别的方式求解子问题
主问题产生的解
子问题产生的割，图中“C”指普通的割，“I”指改进的割，“C/I”指普通的最优割，改进的可行割。

从求解过程优化

主问题和子问题迭代求解是主要的计算瓶颈之一，MP经常通过B&B来求解，子问题则用单纯形法。

MP层面

在BD算法中，往往90%的时间都花在求解MP上[3]。一般会从两个角度来降低其影响：问题规模算法本身。

限制问题规模

在任何MP的最优解中，有效的约束数量总是不超过决策变量的数量，因此，大部分产生的割都不会对算法的收敛起到作用，甚至起反作用（浪费计算时间与内存）。所以，割的清除策略也很重要，特别是每次迭代中都增加多组割的时候。然而并没有成熟的办法来鉴定一个割是否有用，所以往往割的清理删除策略都是启发式的，当一个约束的松弛变量太大的时候，则可以被移除，要注意被移除的割不应被重复加入MP。

有时，多个割会被加入MP，但是并不是全部都有用，[4]中提出如果当前的解绝对小于当前已知最好上界时，这时可以产生相对好的割。[5]中选择根据到不同的内点的距离，选择更紧的割。总的来说，这些方法通过移除不重要的割或者限制不必要割的加入来控制MP的问题规模，然而效果并不是很显著，一方面是会带来额外的难度来计算割的好坏，同时启发式的方法会移除一些有用的割。

算法本身改进

在求解MP问题中，每次迭代中并不需要求得最优解来得到全局的收敛，一些研究关注于如何快速找到次优解，其他的则关注于利用MP结构的优势高效求解。[6]中第一次指出计算MP的难度，他们发现迭代中每步求解MP的最优来产生割并不是必要的。实际中，在算法开始的时候并不需要这样做，所以他们求解MP问题采用\(\epsilon\text{-optimality}\)的策略。

我们也可以选择通过启发式来求解MP，这样不仅可以减少时间，还可以在每次迭代中产生多组割，更快的提高下界[7]。

约束规划（Constraint Programming）也是一种可行的方式[8]，但我对CP了解不多，也不赘述了。

列生成（Column Generation）算法也是一个求解MP问题的很好的选择，用CG来更高效地处理确定结构的问题，在根节点上更紧的bounds。[9]中提出利用BD来处理约束之间的连接，来处理航空路线规划和人员调度问题，将该问题处理成路径规划的主问题和一个人员配对的子问题。同时可以参考[10,11]。

在传统的BD算法中，主问题往往是利用B&B来求解，在迭代中，往往会花很多时间来访问之前被否决掉的节点，所以可以建立一个搜索树，并通过产生有效割来寻找最优解，这样的策略被称为Branch-and-Benders-cut（B&BC）。

子问题层面

子问题往往是规模很大的LP问题，[12]中表明子问题对偶问题的次优解也能产生有效的割，同时这些不精确的解的计算难度很低，却能产生很好的效果。[5]中提到这样的做法有可能会导致错误的解，因为有非极点的割加入MP，但[12]中inexact benders cuts却可以保证收敛。

同时CG也可以应用于子问题求解，对于特殊结构的问题，也可能会存在解析解。当子问题可以被分离时候，可以并行求解多个子问题。

优化子问题产生的割

迭代的次数与产生的割的强度是强相关的，以前有很多文章都有研究如何选择较强的割或者产生额外的有效割。

[3]是第一个考虑子问题退化情况的，当对偶子问题有多个最优解的时候，会产生并不同的割，文中提出Pareto-optimality割的概念，一个pareto-optimal的解会在核点（core point）处得到最大值，在解决常规的对偶子问题后，作者增加了一个辅助子问题来找pareto-optimal 最优割： \[ \max_{\pi\in \mathbb{R}^{m_2}}\lbrace \pi^T(d-B\hat{y}): \pi^TD\leq c, \pi^T(d-B\bar{y})=Q(\bar{y}) \rbrace \] 其中\(Q(\bar{y})\)表示对于主问题给定的\(\bar{y}\)，常规子问题的最优花费。这样做虽然很高效，但仍然带来了多余计算量，同时很难去找到核点，后续文章[13,14,15,16]都是基于此的改进。

[17]中提出一种针对于0-1变量的组合割（combinatorial benders cuts），是一种改进的可行割，作者发现由于大M的约束，产生的割会很弱，而这种方法可以有效提高模型的表现。[5]发现由于选择弱的可行割，会造成算法整体的收敛速度漫，所以提出了一种精确的更紧可行割，扩展了pareto-optimal cuts的概念，将其用于feasibility cuts上，根据可行点和不可行点，找出较合适的割加入子问题，效果提升的同时也带来了很多额外的计算。

还有很多关注于其他方面的，[19]中关注了产生的割一般是low-density的问题，MP中大部分变量在这些割中的系数都是0，这样的割就很弱，作者提出一种covering cut bundle cut-generation的方法，每次迭代产生多个割，这样一组割的cover程度高，有助于提高收敛速度（作者在文中指出，多个low-density的割效果比单个high-density的割效果好）。[20]中作者提出一种更少的计算量的方法，可以cover所有MP中的变量。[21]中关注了很难找到optimality cut的情况，通过求解一个最大可行问题（MFS，maximal feasible subsystem）来产生optimality cuts，[18]也采用相似的做法。

通过分解策略来优化

[22]中指出BD使得MP问题失去了简单变量的信息，所以提出了一种局部分解的策略。除此之外还有一些非标准的分解方式，我不是很了解就不在此罗列了，详细可以参考[1]的全文。

优化主问题产生的解

复杂决策变量的解的质量直接决定了迭代的次数，有三种方式来改善解的质量或提高求解速度：

使用非传统的形式
改善MP的形式
用启发式得到解或者改善已经找到的解

使用非传统的形式

[23]中指出从MP的LP松弛中也可以产生有效的割，所以将BD算法分成两个阶段，第一个阶段快速产生解，然后再加上整数的约束。[24]提出一种交叉分解的方式，将拉格朗日松弛和BD结合，给定整数变量\(y\)可以从BD的子问题求出拉格朗日乘子\(\pi\)，然后根据\(\pi\)，求解拉格朗日子问题产生新的\(y\)。这样的交替结束后，两个子问题的解都可以用来产生新的割给主问题。

优化主问题

优化住问题最有效的办法就是增加有效不等式，增加有效不等式来得到更紧的MP，同时当子问题可分的时候，也可以从每个子问题中都产生割来加入到MP中。

启发式

启发式可以作为“热启动”（warm-start）策略，在初始就得到一些约束较紧的割。同时启发式也可以用来生成解的近邻解作为一种增强策略。

Benders Decomposition 总结

总的来说BD是一种求解大规模MIP问题的利器，是一种基于松弛和投影的求解方式，一种聪明的加割的方式，某种程度上与分之定界类似，MP的求解依赖于最优割（分之定界法的可行解的作用，提供下界），而MP的求解就是松弛问题不断被压紧的过程（多种割来割掉解的空间，类似于分之定界的LP松弛通过不断branch而解空间缩小）。

说点我的直观感受，我一直觉得割平面法是一种从外往内找最优解的过程，而分之定界框架是一种由内到外找最优的方法，而BD就是提供了一种迭代的“割平面”框架。

参考

Rahmaniani, Ragheb, et al. “The Benders Decomposition Algorithm: A Literature Review.” European Journal of Operational Research, vol. 259, no. 3, Elsevier B.V., 2017, pp. 801–17, doi:10.1016/j.ejor.2016.12.005.
Benders, Jacques F. "Partitioning procedures for solving mixed-variables programming problems." Numerische mathematik 4.1 (1962): 238-252.
Magnanti, Thomas L., and Richard T. Wong. "Accelerating Benders decomposition: Algorithmic enhancement and model selection criteria." Operations research 29.3 (1981): 464-484.
Rei, Walter, et al. "Accelerating Benders decomposition by local branching." INFORMS Journal on Computing 21.2 (2009): 333-345.
Yang, Yu, and Jong Min Lee. "A tighter cut generation strategy for acceleration of benders decomposition." Computers & Chemical Engineering 44 (2012): 84-93.
Geoffrion, Arthur M. "Generalized benders decomposition." Journal of optimization theory and applications 10.4 (1972): 237-260.
Raidl, Günther R. "Decomposition based hybrid metaheuristics." European journal of operational research244.1 (2015): 66-76.
Benoist, Thierry, Etienne Gaudin, and Benoît Rottembourg. "Constraint programming contribution to benders decomposition: A case study." International Conference on Principles and Practice of Constraint Programming. Springer, Berlin, Heidelberg, 2002.
Cordeau, Jean-François, et al. "Benders decomposition for simultaneous aircraft routing and crew scheduling." Transportation science 35.4 (2001): 375-388.
Mercier, Anne, Jean-François Cordeau, and François Soumis. "A computational study of Benders decomposition for the integrated aircraft routing and crew scheduling problem." Computers & Operations Research 32.6 (2005): 1451-1476.
Restrepo, María I., Bernard Gendron, and Louis-Martin Rousseau. Combining Benders decomposition and column generation for multi-activity tour scheduling. CIRRELT, 2015.
Zakeri, Golbon, Andrew B. Philpott, and David M. Ryan. "Inexact cuts in Benders decomposition." SIAM Journal on Optimization 10.3 (2000): 643-657.
Papadakos, Nikolaos. "Practical enhancements to the Magnanti–Wong method." Operations Research Letters 36.4 (2008): 444-449.
de Sá, Elisangela Martins, Ricardo Saraiva de Camargo, and Gilberto de Miranda. "An improved Benders decomposition algorithm for the tree of hubs location problem." European Journal of Operational Research 226.2 (2013): 185-202.
Fortz, Bernard, and Michael Poss. "An improved benders decomposition applied to a multi-layer network design problem." Operations research letters 37.5 (2009): 359-364.
Naoum-Sawaya, Joe, and Samir Elhedhli. "An interior-point Benders based branch-and-cut algorithm for mixed integer programs." Annals of Operations Research 210.1 (2013): 33-55.
Codato, Gianni, and Matteo Fischetti. "Combinatorial Benders' cuts for mixed-integer linear programming." Operations Research 54.4 (2006): 756-766.
Fischetti, Matteo, Domenico Salvagnin, and Arrigo Zanette. "A note on the selection of Benders’ cuts." Mathematical Programming 124.1-2 (2010): 175-182.
Saharidis, Georgios K. D., et al. “Accelerating Benders Method Using Covering Cut Bundle Generation.” International Transactions in Operational Research, vol. 17, no. 2, 2010, pp. 221–37, doi:10.1111/j.1475-3995.2009.00706.x.
Saharidis, Georgios K. D., and Marianthi G. Ierapetritou. “Speed-up Benders Decomposition Using Maximum Density Cut (MDC) Generation.” Annals of Operations Research, vol. 210, no. 1, 2013, pp. 101–23, doi:10.1007/s10479-012-1237-8.
Saharidis, G. K. D., and Marianthi G. Ierapetritou. “Improving Benders Decomposition Using Maximum Feasible Subsystem (MFS) Cut Generation Strategy.” Computers and Chemical Engineering, vol. 34, no. 8, 2010, pp. 1237–45, doi:10.1016/j.compchemeng.2009.10.002.
Crainic, Teodor Gabriel, Mike Hewitt, and Walter Rei. Partial decomposition strategies for two-stage stochastic integer programs. CIRRELT, 2014.
McDaniel, Dale, and Mike Devine. "A modified Benders' partitioning algorithm for mixed integer programming." Management Science 24.3 (1977): 312-319.
Van Roy, Tony J. “Cross Decomposition for Mixed Integer Programming.” Mathematical Programming, vol. 25, no. 1, 1983, pp. 46–63, doi:10.1007/BF02591718.