Example Online Optimizers
对于FTL(Follow-The-Leader)算法, \[ \mathbf{w}_{t+1}=\underset{\mathbf{w}\in\mathcal{W}}{\arg\min}\sum^t_{s=1}f_s(\mathbf{w}) \equiv=\underset{\mathbf{w}}{\arg\min}f_{1:t}(\mathbf{w}) \] 当\(f_t\)是线性函数的时候,FTL算法最坏的可能悔恨为\(\mathcal{O}(T)\)。
对于另一个算法BTL(Be-The-Leader,不可实现,因为它利用了未来的信息),相比于FTL,在\(t\)轮的时候使用了\(\mathbf{w}_{t+1}\)。
定理1:对于任何有界的\(f_t\),\(\text{Regret}(\text{BTL})\leq 0\),即\(\sum^T_{t=1}f_t(\mathbf{w}_{t+1})\leq\sum^T_{t=1}f_t(\mathbf{w}_{T+1})\)。
证明:
当\(T=1\)时,\(f_1(\mathbf{w}_2)\leq f_1(\mathbf{w_2})\)显然成立,则对于\(T>1\)时, \[ \begin{aligned} \sum^{T+1}_{t=1}f_t(\mathbf{w}_{t+1}) &= \sum^{T}_{t=1}f_t(\mathbf{w}_{t+1}) + f_{T+1}(\mathbf{w}_{T+2})\\ &\leq \sum^{T}_{t=1}f_t(\mathbf{w}_{T+1}) + f_{T+1}(\mathbf{w}_{T+2})\\ &\leq \sum^{T}_{t=1}f_t(\mathbf{w}_{T+2}) + f_{T+1}(\mathbf{w}_{T+2})\\ &= \sum^{T+1}_{t=1} f_t(\mathbf{w}_{T+2}) \end{aligned} \] 由以上归纳法证得。\(\Box\)
定理2:对于\(\forall w^*\in\mathcal{W}\),当\(f_t\)有界时,有 \[ \text{Regret}(\text{FTL})\leq \sum^{T}_{t=1}(f_t(\mathbf{w}_t)-f_t(\mathbf{w}_{t+1})) \]
证明: \[ \begin{aligned} \text{Regret}(\text{FTL}) &= \sum^T_{t=1}f_t(\mathbf{w}_t)-\sum^T_{t=1}f_t(\mathbf{w}^*)\\ &\leq \sum^T_{t=1}f_t(\mathbf{w}_t)-\sum^T_{t=1}f_t(\mathbf{w}_{T+1})\\ &= \sum^T_{t=1}f_t(\mathbf{w}_t)-\sum^T_{t=1}f_t(\mathbf{w}_{T+1}) + \sum^T_{t=1}f_t(\mathbf{w}_{t+1})-\sum^T_{t=1}f_t(\mathbf{w}_{t+1}) \\ &= (\sum^T_{t=1}f_t(\mathbf{w}_{t+1})-\sum^T_{t=1}f_t(\mathbf{w}_{T+1}))+ (\sum^T_{t=1}f_t(\mathbf{w}_t) -\sum^T_{t=1}f_t(\mathbf{w}_{t+1}))\\ &= \text{Regret}(\text{BTL}) + (\sum^T_{t=1}f_t(\mathbf{w}_t) -\sum^T_{t=1}f_t(\mathbf{w}_{t+1}))\\ &\leq \sum^T_{t=1}f_t(\mathbf{w}_t) -\sum^T_{t=1}f_t(\mathbf{w}_{t+1}) \end{aligned} \] 证毕。\(\Box\)
Transformations in Online Optimization
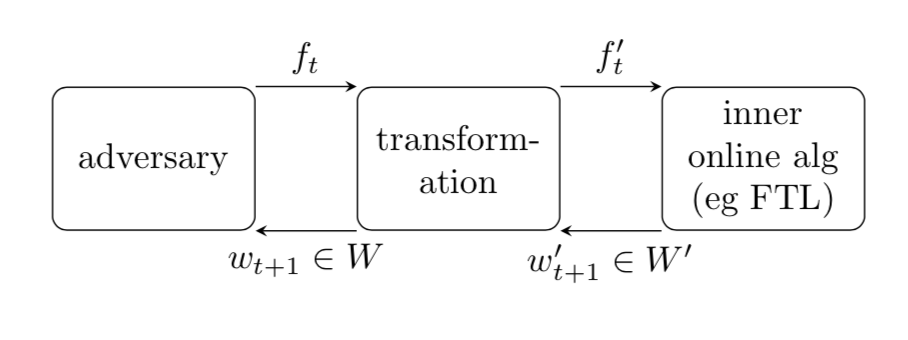
如上图所示,FTRL(Follow-The-Regularized-Leader,著名的在线 CTR预估模型)就是利用了这种转换,将FTL算法用在一个带正则项的损失函数上,每一轮的迭代式为 \[ \mathbf{w}_{t+1}=\underset{\mathbf{w}}{\arg\min}(f_{1:t}(\mathbf{w})+r(\mathbf{w})) \] 其中正则项函数\(r:\mathbb{R}^n\rightarrow\mathbb{R}\),满足\(r(\mathbf{w})\geq 0\),\(r(0)=0\)。
FTRL算法可以看作是在FTL算法的基础上做如下转换:给定函数\(f_t(\mathbf{w})\),令\(f'_t(\mathbf{w})=\mathbf{g}_t\cdot\mathbf{w}+r(\mathbf{w})\),然后令\[f'_t=f_t\]。
定理3:FTRL算法的悔恨界为 \[ \text{Regret}(\text{FTRL})\leq\sum^T_{t=1}(f_t(\mathbf{w}_t)-f_t(\mathbf{w}_{t+1})) +r(\mathbf{w}^*) \]
证明: \[ \begin{aligned} \sum_tf'_t(\mathbf{w}_t)-\sum_tf'_t(\mathbf{w}^*) &\leq \sum_tf'_t(\mathbf{w}_t)-\sum_tf'_t(\mathbf{w}_{t+1})\\ \sum_tf_t(\mathbf{w}_t)-\sum_tf_t(\mathbf{w}^*)+r(\mathbf{w}_1)-r(\mathbf{w}^*) &\leq\sum_t(f_t(\mathbf{w}_t)-f_t(\mathbf{w}_{t+1}))+r(\mathbf{w}_1)-r(\mathbf{w}_2)\\ \text{Regret}(\text{FTRL}) &\leq \sum_t(f_t(\mathbf{w}_t)-f_t(\mathbf{w}_{t+1}))+r(\mathbf{w}^*)-r(\mathbf{w}_2)\\ \text{Regret}(\text{FTRL}) &\leq \sum_t(f_t(\mathbf{w}_t)-f_t(\mathbf{w}_{t+1}))+r(\mathbf{w}^*) \end{aligned} \] 证毕。\(\Box\)
FTRL对于线性的\(f_t\):
- \(f_t(\mathbf{w})=\mathbf{g}_t\cdot\mathbf{w}\)
- \(\|\mathbf{g}_t\|\leq G\)(有界)
- \(\mathbf{w}_{t+1}=\underset{\mathbf{w}}{\arg\min}(\sum_t\mathbf{g}_t\cdot\mathbf{w}+\frac{\sigma}{2}\|\mathbf{w}\|^2)\),其中\(\sigma\in\mathbb{R}^+\)(二次正则项)
那么我们就有 \[ \begin{aligned} \text{Regret}(\text{FTRL}) &\leq \sum^T_{t=1}(f_t(\mathbf{w}_{t})-f_t(\mathbf{w}_{t+1}))+r(\mathbf{w}^*)\\ &=\sum_t\mathbf{g}_t\cdot(\mathbf{w}_t-\mathbf{w}_{t+1}) + r(\mathbf{w}^*)\\ &\leq \sum_t\|\mathbf{g}_t\|\|\mathbf{w}_t-\mathbf{w}_{t+1}\| +\frac{\sigma}{2}\|\mathbf{w}^*\|^2 \\ &\leq \sum_t G \|\mathbf{w}_t-\mathbf{w}_{t+1}\| +\frac{\sigma}{2}\|\mathbf{w}^*\|^2 \\ \end{aligned} \] 此时我们,当学习率为\(\frac{1}{\sigma}\)时,采用梯度下降法时,我们有 \[ \begin{aligned} \mathbf{w}_{t+1} &=\mathbf{w}_t-\gamma \frac{\part f_{1:t}(\mathbf{w}_t)}{\part \mathbf{w}_t} \\ \mathbf{w}_t-\mathbf{w}_{t+1} &=\frac{-\mathbf{g}_{1:t-1}+\mathbf{g}_{1:t}}{\sigma} =\frac{\mathbf{g}_t}{\sigma} \end{aligned} \] 将其带入上面不等式,得 \[ \begin{aligned} \text{Regret}(\text{FTRL}) &\leq \sum_t G \|\mathbf{w}_t-\mathbf{w}_{t+1}\| +\frac{\sigma}{2}\|\mathbf{w}^*\|^2 \\ &\leq\sum_t G \|\frac{\mathbf{g}_t}{\sigma}\| +\frac{\sigma}{2}\|\mathbf{w}^*\|^2 \\ &\leq \frac{TG^2}{\sigma} +\frac{\sigma}{2}\|\mathbf{w}^*\|^2 \\ \end{aligned} \]
定理4:对于\(\forall \mathbf{w}^*\),当\(\|\mathbf{w}^*\|\leq R\),如果损失函数是线性的\(f_t(\mathbf{w})=\mathbf{g}_t\cdot\mathbf{w}\),且\(\|\mathbf{g}_t\|\leq G\),正则项为\(r(\mathbf{w})=\frac{\sigma}{2}\|\mathbf{w\|^2}\),\(\sigma=\frac{G\sqrt{2T}}{R}\),我们有 \[ \text{Regret}(\text{FTRL})\leq GR\sqrt{2T} \]