Follow the Leader Against Quadratics
某些情况下,FTL是非常好的算法,比如一维的线性回归的情况,很容易推广到高维
- 每一轮选择\(w_t\in[-1,1]\)
- 对手选择\(y_t\in[-1,+1]\)
- 计算\(f_t(w)=\frac{1}{2}(w-y_t)^2\)
\[ 我们的目标就是求 \] w_{t+1}=f_{1:t}(w) \[ 对$w$求导并令导数为$0$,我们有 \] w_{t+1}= $$
定理1:如果\(f\)是一个凸函数,那么\(\forall w,w_t\in\mathcal{W}\),有 \[ \begin{aligned} f(w)& \geq f(w_t)+\triangledown f(w_t)(w-w_t) \\ \end{aligned} \]
所以我们有 \[ \begin{aligned} f(w_t) - f(w_{t+1}) & \leq \triangledown f(w_t)(w_t-w_{t+1}) \\ &\leq \|\triangledown f(w_t)\|\|w_t-w_{t+1}\| \end{aligned} \] 我们可以发现上述不等式右边,第一项小于梯度的界,第二项小于两次迭代间距离的界。现在我们可以计算二次情况下的悔恨值的界 \[ \begin{aligned} w_t-w_{t+1} &= \frac{y_{1:t-1}}{t-1}-(\frac{y_{1:t-1}}{t-1}\cdot\frac{t-1}{t}+\frac{y_t}{t})\\ &=\frac{y_{1:t-1}}{t(t-1)}-\frac{y_t}{t}\\ &\leq \frac{t-1}{t(t-1)}+\frac{1}{t}\\ &\leq \frac{2}{t} \end{aligned} \] 其中第三步是因为\(y_t\in[-1,+1]\),所以可以得到悔恨的界为 \[ \text{Regret} \leq\sum_t f_t(w_t)-f_t(w_{t+1}) \leq\sum_t2(\frac{2}{t}) \leq4\sum_t\frac{1}{t} \leq 4(\log(T)+1) \]
Playing Against Linear Functions
Linearizing Convex Functions
线性化一个凸函数会让在线学习变得更难,对于任意\(w^*\),\(g_t\in\part f_t(w_t)\), \[
\begin{aligned}
w^* &= \underset{w\in\mathcal{W}}{\arg\min}f_{1:t}(w^*) \\
\text{Regret}(T)
&= f_{1:t}(w_t)-f_{1:t}(w^*)\\
&=\sum^T_{t=1}[f_t(w_t)-f_t(w^*)]\\
&\leq \sum^T_{t=1}[w_t\cdot g_t-w^*\cdot g_t]
\end{aligned}
\] 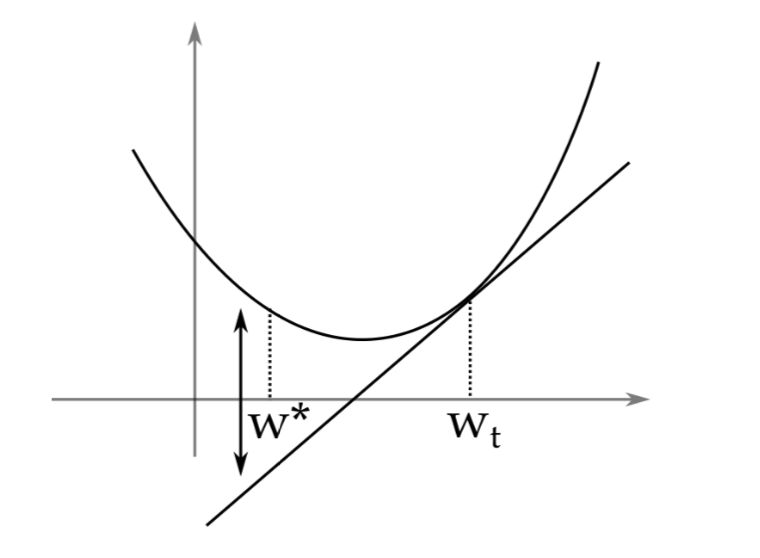
正如上图所示,用线性近似的话,其他选择的损失是被降低的,因此会导致悔恨的增加。因此,线性情况下的悔恨(linearized regret)是凸函数情况下的悔恨(convex regret)的上界。使用这个性质,通过变换凸在线学习问题到线性在线学习问题,我们可以得到有界的悔恨值。线性情况下,我们最优的情况是\(\sqrt{T}\)的悔恨,在有严格凸的假设下,可以做得更好。
定义1:一个函数\(f:\mathbb{R}^n\rightarrow\mathbb{R}\),如果\(\forall w, w'\in\mathbb{R}^n\),有 \[ \|f(w)-f(w')\|\leq G\|w-w'\| \] 那么这个函数\(f\)是G-Lipschitz的。
定理2:对于一个凸函数\(f:\mathbb{R}^n\rightarrow\mathbb{R}\),如果是G-Lipschitz,当且仅当对于\(\forall w\in\mathbb{R}^n\),\(\forall g\in\part f_t(w_t)\),有\(|g|\leq G\)。
证明:
必要性,选择\(w\in\mathcal{W}\),\(g\in\part f_t(w_t)\), \[ G\|w-w-\frac{g}{\|g\|}\|\geq f(w+\frac{g}{\|g\|})-f(w) \] 根据次梯度的定义 \[ f(w+\frac{g}{\|g\|})-f(w) \geq (w+\frac{g}{\|g\|}-w)g =\frac{g\cdot g}{\|g\|} =\|g\| \] 充分性,选择\(w'\in\mathcal{W}\),\(g\in\part f_t(w_t)\) \[ f(w')-f(w)\leq(w'-w)\cdot g\leq\|w'-w\|\cdot\|g\|\leq\|w'-w\|G \] 证毕。\(\Box\)
所以当我们用一个凸的Lipschitz函数时候,FTRL可以达到\(\mathcal{O}(\sqrt{T})\)的悔恨值。