最近要写几个滴滴相关的论文的笔记,顺便解读一下目前的拼车算法等策略,顺带着科普。今天这篇是KDD2017的《A Taxi Order Dispatch Model based On Combinatorial Optimization》,这篇文章是比较早时候的分单算法的文章,跟现在的算法略有差异。
简介
传统的拼车算法是一种顺序的分配策略,在乘客周围选择最近的车辆,最大化每个司机对每个订单的接受概率,这样做有可能会导致一个较低的全局匹配成功率,本篇文章中提出了一种最大化全局的匹配概率的方法,改善用户体验,同时文中还提出一种基于贝叶斯框架的预测用户目的地的方法。
订单分配系统
我们的目标是最大化匹配成功率,记为\(E_{SR}\),\(N\)个订单分配给\(M\)个司机,分配结果矩阵为 \[ \left\{ \begin{matrix} a_{11} & \cdots & a_{1M} \\ \cdots & a_{ij} & \cdots \\ a_{N1} & \cdots & a_{NM} \end{matrix} \right\} \] 期中\(1\leq i\leq N\),\(1\leq j \leq M\),当\(a_{ij}=1\)的时候表示订单\(i\)分配给司机\(j\),在这种场景中,每个司机最多只能接一个订单,所以\(\forall j,\sum^N_{i=1}a_{ij}\leq1\)。在每轮的分配中,每个订单会分配给一些司机,每个司机根据自己的意愿决定是否接受这个订单。所以,订单分配的关键问题在于估计每个司机接受这个订单的概率,因此我们把分单模型分成两个子模型,一个模型用来估计司机接受订单的概略,另一个模型用估计的概率来最大化我们的目标\(E_{SR}\)。
预测司机行为模型
我们用\(0-1\)变量\(y\)来表示司机接受或者拒绝,假设每个司机的行为都是独立同分布的。我们用\(p_{ij}\)表示订单\(o_i\)被司机\(d_j\)接受的概率,有很多因素都会影响这个概率,如这一单能赚的钱、行驶距离、目的地等等,这些因素记为特征向量\(\bf{x_{ij}}\),则接受概率可以表示为 \[ p_{ij}=p(y=1|\bf{x_{ij}}) \] 这个问题可以描述为一个典型的二分类问题,所以我们用历史数据进行模型训练。我们尝试了LR和GBDT,具体效果如下图所示:
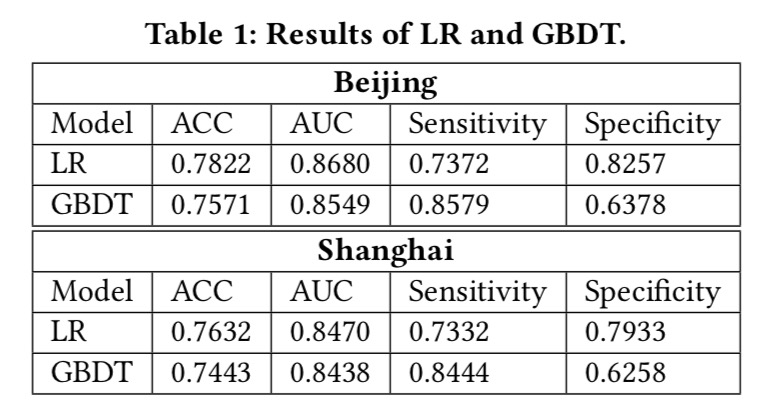
实验结果表明LR的效果稍微好一点,所以我们选择LR作为预测模型,采用SGD训练模型。特征方面主要包括四方面:
- 订单-司机相关的特征,接人的距离、订单通知司机数量、订单是否在司机的行驶方向上等等;
- 订单相关特征,距离和ETA、目的地类型、路线上交通情况等等;
- 司机相关特征,司机长期表现、司机之前接受订单概率、司机行驶偏好等等;
- 附加特征,天气、时间、周围司机和订单数等等。
组合优化模型
假设\(N\)个订单需要被分配,订单\(i\)被接受的概率为: \[ E_i=1-\prod_{j=1}^M(1-p_{ij})^{a_{ij}} \] 其中\(p_{ij}\)就是之前估计的骑手接受概率,所以我们可以把我们的全局目标表示出来: \[ E_{SR}=\frac{\sum^N_{i=1}[1-\prod_{j=1}^M(1-p_{ij})^{a_{ij}}]}{N} \] 其中还有约束为: \[ \sum^N_{i=1}a_{ij}\leq 1,\forall j \] 这样的组合优化问题往往是NP-Hard的,通常采用启发式的方式求解,如爬山法、遗传算法、模拟退火等等。为了平衡精确度和算法的性能,我们选择爬山算法来求解这个问题:

目的地预测
通过长期的观察,我们发现几个有趣的现象:
- 同一个乘客会在相近的时间去同一个目的地;
- 同一个乘客会去固定几个地方;
- 订单的位置会对目的地的预测提供很多有效的信息。
鉴于以上几个现象,我们先将时间划分成工作日和节假日两个部门,工作日的目的地通常是家或者公司,节假日则更多的是购物中心或者娱乐场所,我们发现贝叶斯模型会更适合这样的场景。我们先做如下的标记:
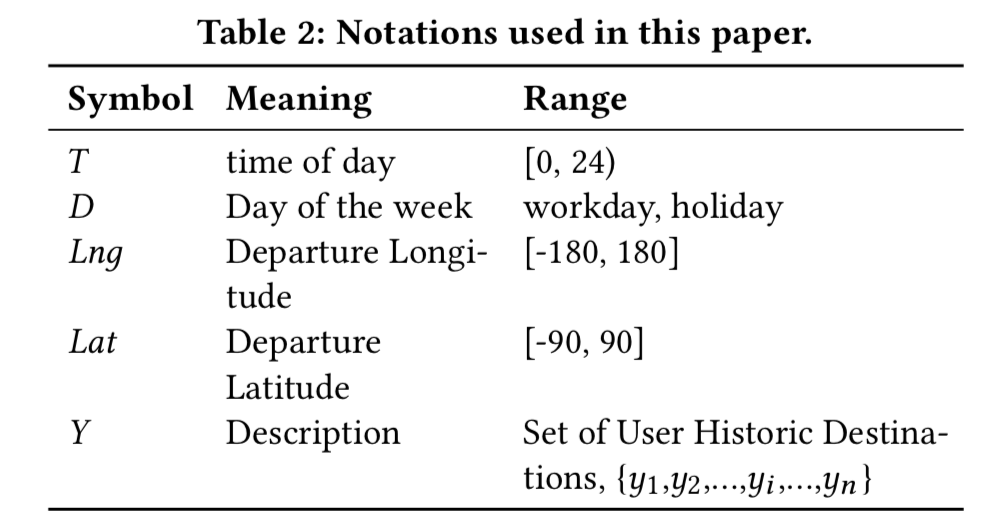
因为\(D\)仅有两类,所以我们先以此把用户历史数据划分成两类,除此之外,我们根据时间对训练的历史数据进行加权,削弱历史对现在的影响。我们定义如下贝叶斯模型: \[ p(Y=y_i|X)=\frac{p(X|Y=y_j)p(Y=y_j)}{\sum^n_{j=1}p(X|Y=y_j)p(Y=y_j)} \] 其中\(X=(T,Lng,Lat)\)表示出发时间、经度和纬度。我们用乘客的历史数据估计\(p(Y=y_j)\): \[ p(Y=y_j)=\frac{\text{freq}(y_j)}{\sum^n_{j=1}\text{freq}(y_j)} \] 剩下的问题就是如何去估计出发时间和位置的联合分布了。通过分析数据,我们发现给定\(y_j\)之后,时间的分布近似正态分布,因此我们用正态分布来估计出发时间的条件概率 \[ T|Y=y_i\sim N(\mu_i,\sigma_i^2) \] 因为时间变量是从\(0-23\)变化然后重复的,所以\(\mu_i\)和\(\sigma_i\)并不能用传统的方式进行估计,比如如果时间是8:00,9:00,10:00,他们的均值就是9:00,但是如果是3:00,15:00,21:00,,他们的均值是21:00,而不是\((3+15+21)/3=13\)。时间变量是一个循环的量,一种常用的方式是将其转化到单位向量上,计算向量的均值,然后再转换回去。给定时间\(t_1,t_2,\cdots,t_m\),他们的均值\(\mu\)可以表示成: \[ \mu=\frac{24}{2\pi}\cdot\arctan[\frac{1}{m}\sum^m_{k=1}\sin(\frac{2\pi}{24}\cdot t_k), \frac{1}{m}\sum^m_{k=1}\cos(\frac{2\pi}{24}\cdot t_k)] \] 这种方法足够简单明了,但会有略微的偏差,比如00:00:00,00:00:00,03:00:00的均值应该是01:00:00,这种方法计算出来是00:58:33。为了解决这个问题,我们提出了另一种计算出发时间均质的方法。出发时间的均值可以表示成如下二次优化问题: \[ \left\{ \begin{aligned} \min_\mu &&& \sum^m_{k=1}[\text{distance}(t_k,\mu)]^2 \\ \text{s.t.} &&& \mu\in[0,24) \end{aligned} \right. \] 其中\(\text{distance}(t_1,t_2)\)表示两个循环变量\(t_1\)和\(t_2\)之间的距离: \[ \text{distance}(t_1,t_2)=\left\{ \begin{aligned} |t_1-t_2| &&& \text{if}\quad |t_1-t_2|\leq12 \\ 24-|t_1-t_2| &&& \text{if}\quad |t_1-t_2|>12 \end{aligned} \right. \] 上面式子可以写为 \[ \text{distance}(t_1,t_2)=-|(|t_1-t_2)-12|+12 \] 则约束问题可以写成 \[ \left\{ \begin{aligned} \min_\mu &&& \sum^m_{k=1}[|(|t_1-t_2|)-12|-12]^2 \\ \text{s.t.} &&& \mu\in[0,24) \end{aligned} \right. \] 通过求解上述问题我们可以得到均值\(\mu\),同样的方法也可以用来估计方差, \[ \sigma^2=\frac{1}{m-1}\sum^m_{k=1}\sum^m_{k=1}[|(|t_1-t_2|)-12|-12]^2 \] 为了找到一个近似的模型来描述三维的联合分布,我们观察了大部分用户的散点图,基本上与三维的高斯分布相同,因此我们假设对于一个给定的用户和一个预期的目的地, \[ Lat,Lng,T|Y=y_j\sim N_3(\pmb{\mu}_i,\Sigma_i) \] 为了证实我们的假设,我们做了正态性检验。完整的计算方法如下:

实验
具体细节参考论文。