这篇文章是用MDP方式去考虑车辆调度的分单算法,发表在KDD2018上,《Large-Scale Order Dispatch in On-Demand Ride-Hailing Platforms: A Learning and Planning Approach》。
这篇文章给我感觉真的是十分精彩,从解决方案到后面实验部分都写的很充实,而且方法朴实却又新颖,作为RL或者说是MDP的一个非游戏类的应用,可以说是很成功的,advantage function的设计很漂亮,真的能体现“数学之美”了。
简介
传统的订单分配方式往往关注于乘客当下的满意度,本文提出一种高效的方式来优化资源的利用效率和全局用户的体验,我们将订单分配作为一个序列决策问题来研究,总体来说分为两部分,第一部分是基于历史数据,我们研究了再时空维度上,供需变化的模式,这个阶段称为Learning,另一部分我们做了一个实时订单-司机对匹配的算法,同时考虑司机当前的收益和未来的收益,这个阶段称为Planning。
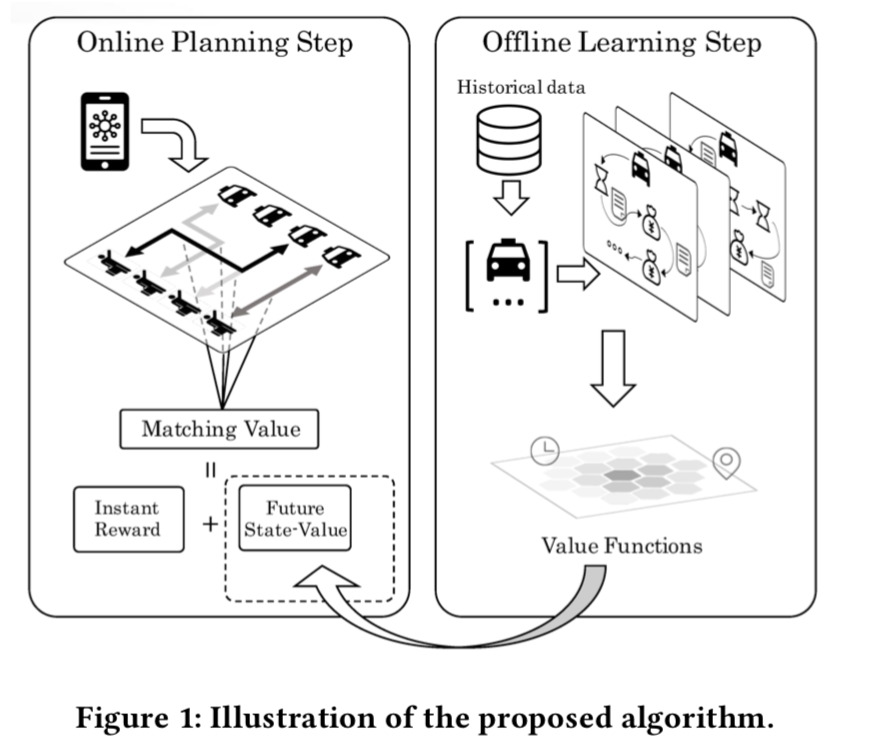
根据滴滴内部的统计数据,从传统的司机选择订单的方式到中心化派单的方式,平台效率会有一个显著的提升,超过10%的订单完成率。传统的订单分配方式,不管是基于位置的局部贪婪匹配法还是基于排队策略先到先服务,这些方法都很容易实现和管理,他们优先满足当前情况下乘客的满意度,由于时空的约束,司机和乘客的供需在时间和空间上是不匹配的,这会导致这些方法在长期上只能取得次优的效果。
我们的目标是在长时间的维度上来优化订单分配过程,既要满足乘客当前的需求,也要考虑未来的收益。我们将这个问题描述成一个序列决策问题,每个司机与订单的匹配决策都依赖于两部分:一部分是当前的收益,另一部分是这个决策在未来的收益。基于乘客的需求和司机的供给的历史数据,我们建立了一个通用的评估方式来评估时空状态(spatiotemporal states)来量化未来的收益,而实时的匹配则是一个组合优化问题。
Learning
Learning阶段目标是学习乘客需求和司机供给之间的一个可量化可理解的时空关系,我们根据历史数据建立了一个MDP模型,得到的价值函数用以刻画每个时空状态下的价值。
MDP通常用来建模序列决策问题,在MDP中,一个agent(翻译成智能体?)在environment(环境)中根据一个policy(策略)来进行行动,每轮次选择一个action(行为),会从当前state(状态)转移到下一个状态,并有一个gain(收益),智能体的目标是最大化长期的收益\(G_t=\sum^T_{i=t}R_{t+1}\),解决MDP通常的做法是寻找一个value function(价值函数),包括state-value function(状态价值函数)\(V_\pi(s)\)和aciton-value function(行为价值函数)\(Q_\pi(s,a)\),其中\(V_\pi(s)=\mathbb{E}_{\pi}[G_t|s_t=s]\),\(Q_\pi(s,a)=\mathbb{E}_\pi[G_t|s_t=s,a_t=a]\)。在我们的场景中,每一个独立的司机我们认为是一个agent,尽管这种设定会导致一个多智能体问题,但相较于把整个平台作为一个智能体,这种设定的优势在于状态的转移、行为和奖励都可以简单地简化定义出来。
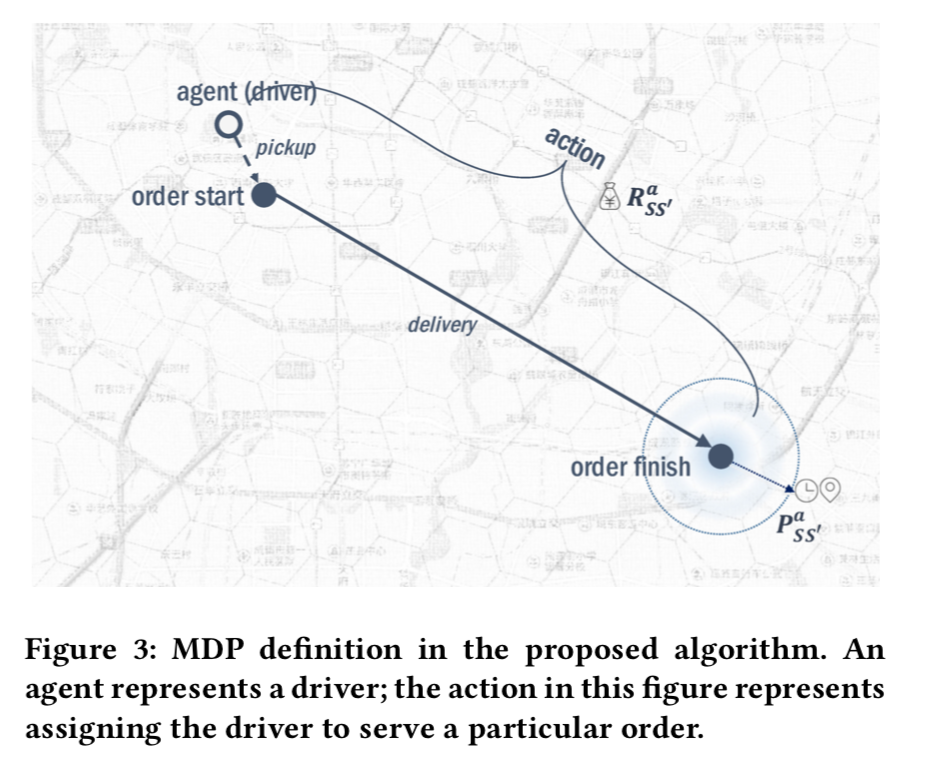
我们继续做以下定义:
- State,状态,每个司机的状态被定义成一个二维的向量,\(s=(t,g),t\in T,g\in G\),其中前者是时间信息,后者是位置信息;
- Action,行为,有两种行为,司机选择去服务一个乘客或者是空跑。司机选择接乘客会产生收益,而空跑则表明这个司机并没有匹配到订单,当司机选择空跑行为时,从一个状态转移到另一个状态,不会产生收益;
- Reward,奖励,定义为GMV;
- State transition,状态转移,定义状态转移概率为\(P_{ss'}^a\);
- Reward distribution,奖励分布,定义奖励分布为\(R_{ss'}^a\);
- Discount factor,折扣因子,折扣因子可以控制MDP对于未来收益的重视程度,在我们的应用中,最好使用较小的折扣因子,因为长时间周期会产生较大的价值函数的方差。定价的价值也应该被降低,对于一个长须时间为\(T\)的订单,价格为\(R\),折扣因子\(\gamma\),最终的奖励为\(R_\gamma=\sum^{T-1}_{t=0}\gamma^t\frac{R}{T}\)。
做个举例,一个司机在A接到一个B到C的订单,时间为00:00,10分钟接乘客,20分钟送乘客,订单收益30元,折扣因子\(\gamma=0.9\),初始状态\(s=(A,0)\),结束状态\(s'=(B,3)\),收益\(r=10+10*0.9+10*0.9^2=27.1\)。
MDP问题的核心就是去做策略的估计,policy evalution。我们将历史交易数据整理成\((s,a,s',r)\)的形式,注意此处我们并不区分司机。我们假设online policy产生交易数据并且保持不变,因此,\(\pi\)在此处为了简洁先不写。一次转移可能从行为“服务乘客”或者是“空跑”中产生,,对于空跑造成的转移,司机并不会立获得当前的奖励,更新表达式为 \[ V(s)\leftarrow V(s) +\alpha[0 + \gamma V(s')- V(s)] \] 其中\(s'=(t+1,g)\),表示下一个时刻司机空跑到的状态,如果是服务乘客,则司机会获得奖励并转移状态 \[ V(s)\leftarrow V(s) + \alpha [R_\gamma + \gamma^{\Delta t}V(s'')-V(s)] \] 其中\(s''=(t+\Delta t, g_{\text{dest}})\)表示结束服务这个乘客时候的司机的状态。\(\Delta t\)表示接乘客、等待和送乘客的总时间,以及\(\Delta t(\text{idle})=1\)。

这种更新方式并不是sample-effcient的,特别是我们这种状态超过百万个的情况,所以我们采用一种动态规划的方式计算价值函数。

Planning
在online planning的阶段,我们利用学到的价值函数作为输入,并且决定哪些司机和哪些订单进行匹配,在每轮匹配中,我们目标也可以认为是为每个司机寻找最好的动作来优化未来全局的收益。
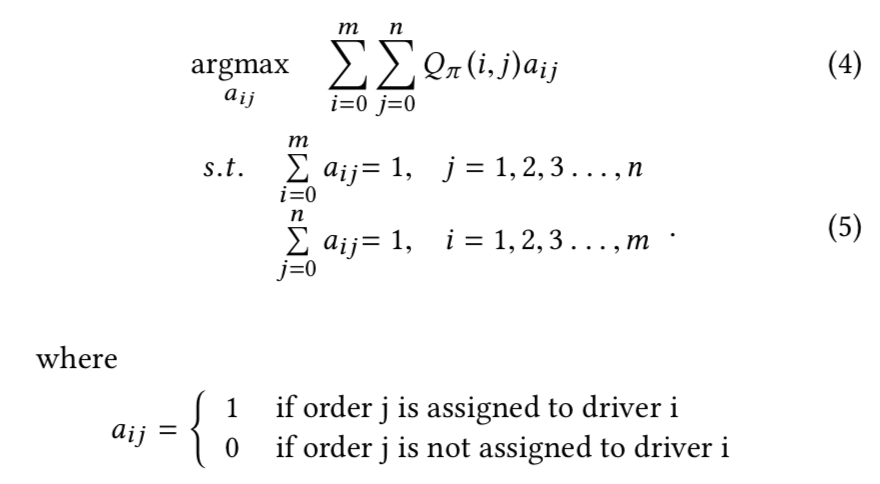
我们采用KM算法来求解上述问题。因为一个司机要么选择接单要么选择空跑,所以这个二分图时完全图,每个边都是可以存在的。为了降低计算的复杂度,我们消除了所有默认行为的边。因为在实践中,每两轮之间的间隔远远小于价值函数中考虑的时间长度,一个司机不做任何行为可以认为是保持在原状态,因此行为价值函数\(Q(i,0)\)实际上等于状态函数,这使得我们可以取消掉所有司机的不作为的动作,这使得边的数量大大减少。
通过上述技巧,模型变成
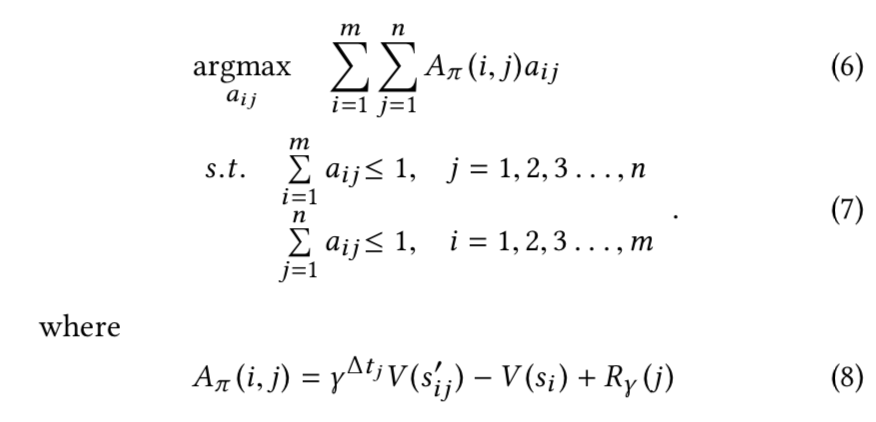
其中\(A_\pi(i,j)\)称为advantage function,这个函数可以通过计算服务乘客的期望收益得出。
我们继续分析advantage function,它包含了我们需要考虑的四个因素:
- 订单价格,高价格订单会更具有优势,\(R_\gamma(j)\);
- 司机位置,司机当前的位置有一个负的影响,\(-V(s_i)\),因此,在相同的条件下,司机在更小价值的位置更容易被选择服务订单;
- 订单目的地,选择高价值地区的目的地的订单更有优势,因为它会有一个更大的\(V(s'_{ij})\);
- 接乘客的距离,接乘客的距离也会影响advantage function,更长的距离需要更多的时间来接乘客,使得订单的未来价值降低,总体的值降低。
除此之外,实际中还会通过一系列超参数,来平衡用户体验和平台效率,达到用户和平台的双赢。
实验部分详见论文。