Scalable Training of L1-Regularized Log-Linear Models

最近重读了一下之前阿里的MLR，又仔细研究了一下里面的优化算法，然后发现也是对之前的一个叫Orthant- Wise Limited-memory Quasi-Newton（下文中称OWL-QN，这个owl让我想起了哈利波特的Ordinary Wizarding Level...）的方法进行的一点小改动，所以今天来读一下OWL-QN的原文。

Introduction

log-linear的模型十分常见，被广泛用于机器学习的各种模型中，经常可以写成以下形式： \[ \min f(x)=\ell(x)+r(x) \] 其中\(\ell\)是negative log-probability（可以理解为负的似然函数），\(r\)为正则项（我们更希望得到简单的模型）。一般在广告CTR领域常用的是L1正则项 \[ r(x)=C\|x\|=C\sum_i |x_i| \] 如果模型是线性模型那么上述形式就成了Lasso，当大部分变量都是不相关的时候，Lasso会得到一个较好的模型估计，产生的稀疏解让模型更具可解释性，同时也对计算更友好。

优良的性质也伴随着种种不便，在0处不可导使得大部分基于梯度的优化算法并不适用于它，包括L-BFGS、拟牛顿法等等，而这些优化算法在有L2正则的大规模log-linear模型上表现优异。

为了方便，先做以下定义，记凸函数\(f:\mathbb{R}^n\mapsto\mathbb{R}\)和向量\(x\in\mathbb{R}^n\)，用\(\partial_i^+f(x)\)表示\(f\)在\(x_i\)处的右导数： \[ \partial_i^+f(x)=\lim_{\alpha\rightarrow0}\frac{f(x+\alpha e_i)-f(x)}{\alpha} \] 其中\(e_i\)表示第\(i\)个分量上的单位向量，同样的方式可以定义左导数\(\partial_i^-f(x)\)。\(f\)在\(x\)的关于方向\(d\in\mathbb{R}^n\)的导数记为\(f'(x;d)\) \[ f'(x;d)=\lim_{\alpha\rightarrow0}\frac{f(x+\alpha d)-f(x)}{\alpha} \] 当\(f'(x;d)<0\)时，方向\(d\)被称为下降方向。符号函数\(\sigma:\mathbb{R}\mapsto\{1,0,-1\}\)表示一个实值的符号，投影函数\(\pi:\mathbb{R}^n\mapsto\mathbb{R}^n\) \[ \pi_i(x;y)=\left\{ \begin{aligned} x_i && \sigma(x_i)=\sigma(y_i) \\ 0 && \text{otherwise}\\ \end{aligned} \right. \]

拟牛顿法和L-BFGS

在介绍OWL-QN之前先回顾一下L-BFGS，与牛顿法相似，拟牛顿法在每一步的迭代中都构造一个二阶近似，然后通过这个近似的二阶函数来搜寻迭代方向。\(\mathbf{B_k}\)表示函数\(f\)在\(x^k\)的Hessian矩阵（或者是近似Hessian矩阵），\(g^k\)表示函数\(f\)在\(x^k\)的梯度，局部的二阶近似函数可以表示成 \[ Q(x)=f(x^k)+(x-x^k)^\mathsf{T}g^k+\frac{1}{2}(x-x^k)^\mathsf{T}\mathbf{H_k}(x-x^k) \] 如果\(\mathbf{B_k}\)是正定的，使得\(Q\)最小的\(x^*\)可以通过下式计算得到 \[ x^*=x^k-\mathbf{H_k}g^k \] 其中\(\mathbf{H_k}=\mathbf{B_k}^{-1}\)，拟牛顿法沿着\(x^k-\alpha\mathbf{H_k}g^k,\alpha\in(0,\infty)\)的方向寻找\(x^{k+1}\)。牛顿法使用精确的二阶导数来做某个点处的二阶泰勒展开，拟牛顿法则是使用之前探索过的点的一阶导的信息来近似的Hessian矩阵，L-BFGS，最多使用之前m个点的信息，即在第\(k\)步，存储\(s^k=x^k-x^{k-1}\)和\(y^k=g^k-g^{k-1}\)，忽略最开始的\(k-m\)轮迭代的数据，然后根据\(\{s^i\}\)和\(\{y^i\}\)来估计\(\mathbf{H_k}\)，因为完整的Hessian矩阵可能太大难以计算，也可以选择直接估计\(-\mathbf{H_k}g^k\)。

Orthant-Wise Limited-memory Quasi-Newton

假设损失函数\(\ell\)为凸，有阶，连续可导，梯度\(\triangledown\ell\)为L-Lipschitz连续的，我们的目标是最小化\(f(x)=\ell(x)+C\|x\|_1\)。OWL-QN的想法来自于对L1正则的思考：给定任意象限的一些点，如果这些点不改变象限，那么目标函数就是可微的，所以带正则项的目标函数\(f\)的二阶情况取决于每一部分的loss。对于任意符号向量\(\xi\in\{-1,1,0\}^n\)，定义 \[ \Omega_\xi=\{x\in\mathbb{R}^n:\pi(x;\xi)=x\} \] 其为某些象限和某些坐标为0的超平面的交集，对于任意\(x\in\Omega_\xi\)， \[ f(x)=\ell(x)+C\xi^\mathsf{T}x \] 定义\(f_\xi\)为这个函数在\(\mathbb{R}^n\)上的扩展，用L-BFGS的近似\(\mathbf{H_k}\)来近似损失函数的Hessian矩阵，\(v^k\)为函数\(f_\xi\)在\(x^k\)的负梯度在自空间\(\Omega_k\)上的投影，则在空间\(\Omega_k\)上可以得到\(f_\xi\)的二阶近似\(Q_\xi\)，此处我们限制搜索方向为 \[ p^k=\pi(\mathbf{H_k}v^k;v^k) \]

象限选择

在迭代的时候，给定迭代的点\(x^k\)，有太多相邻或者包含这个点的象限，为了确定下次迭代探索哪个象限，我们定义函数\(f\)在\(x\)处的伪梯度（pseudo-gradient） \[ \diamond f(x)=\left\{ \begin{aligned} \partial_i^-f(x) && \text{if }\partial_i^-f(x)>0\\ \partial_i^+f(x) && \text{if }\partial_i^+f(x)<0\\ 0 && \text{otherwise} \end{aligned} \right. \] 此处解释一下，当左导数大于0的时候，向左是下降方向，右导数小于零，向右是下降方向，否则，梯度为0，如下图所示

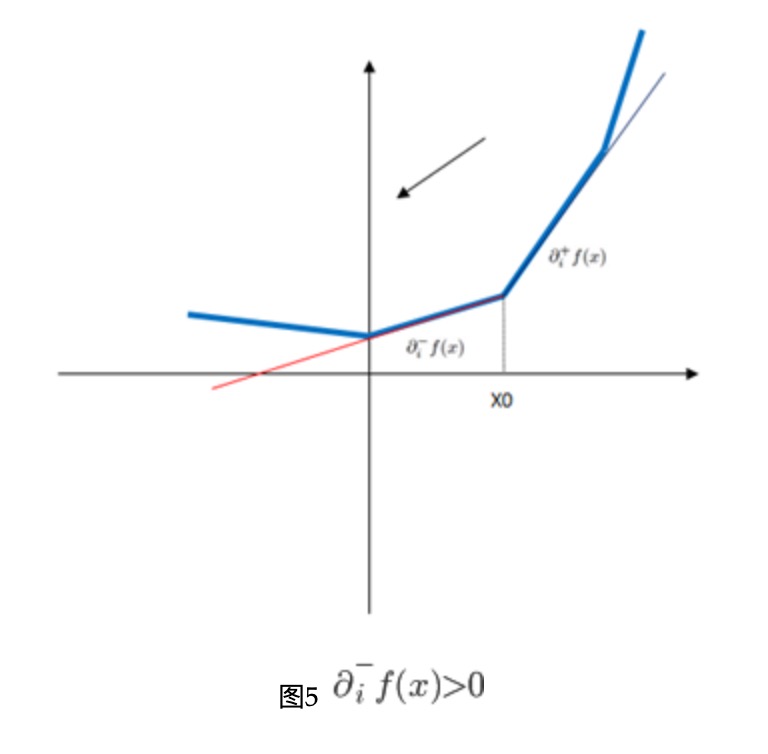
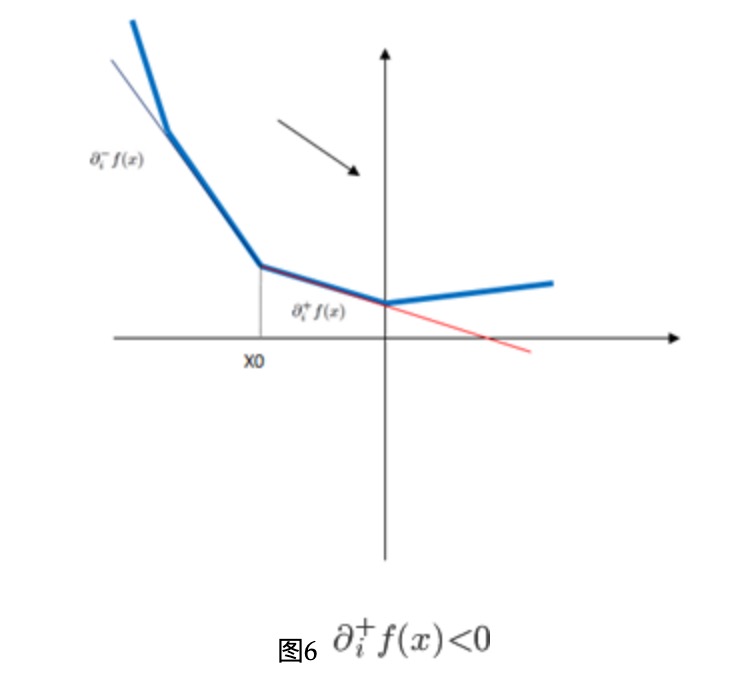
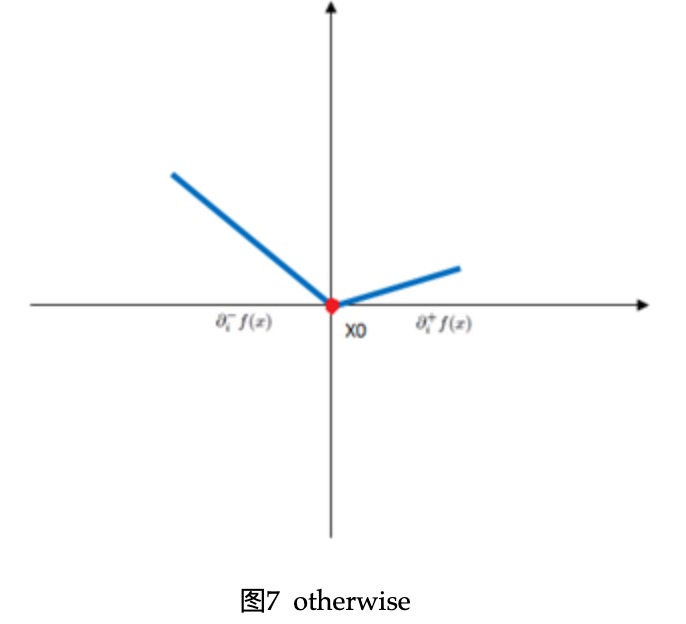
\(f\)的左右偏导为 \[ \partial_i^{\pm}f(x)=\frac{\partial}{\partial x_i}\ell(x)+\left\{ \begin{aligned} C\sigma(x_i) && \text{if } x_i\neq0\\ \pm C && \text{if } x_i=0 \end{aligned} \right. \] 注意此处有\(\partial_i^-f(x)\leq\partial_i^+f(x)\)。当需要选择下一个象限去探索的时候，选择包含\(x^k\)且伪梯度所指向的方向： \[ \xi_i^k=\left\{ \begin{aligned} \sigma(x_i^k) && \text{if } x_i^k\neq0\\ \sigma(-\diamond_if(x^k)) && \text{if } x_i^k=0 \end{aligned} \right. \] 这样选择方式使得\(-\diamond_if(x^k)\)等于\(v^k\)，\(f_\xi\)在\(x^k\)处的负梯度对于空间\(\Omega_\xi\)投影。

带约束的线搜索（line search，感觉一维搜索更贴切）

在搜索下一个点\(x^{k+1}\)的时候，为了确保不离开\(Q_\xi\)的可行域，我们将所有探索的点投影回\(\Omega_\xi\) \[ x^{k+1}=\pi(x^k+\alpha p^k;\xi^k) \] 超过边界的点的坐标都会被置为0。\(\alpha\)可以用很多方法进行设置，论文中采用的是回溯线搜索，选择任意常量\(\beta,\gamma\in(0,1)\)，对于\(n=0,1,2,\cdots\)，\(\alpha=\beta ^n\)，选择第一个使得下式成立的\(n\)： \[ f(x^{k+1})\leq f(x^k)-\gamma v^\mathsf{T}(x^{k+1}-x^k) \] 完整的OWL-QN算法描述如下图

相较于标准的L-BFGS，仅有几个不同：

伪梯度\(\diamond f(x)\)替代梯度
线搜索方向需要与伪梯度一致，保持象限不变
下一个所选择的点与当前点的象限一致
构造\(y^k\)的时候采用不带正则项损失函数的梯度（L1正则项不影响Hessian矩阵的估计）

总结

此处列举这篇文章的几个关键点：

利用了L1正则在某个象限中可导的性质
利用伪梯度选择方向（左右偏导）
单次搜索不跨越象限