[KDD2019] A Unified Framework for Marketing Budget Allocation
这次是kdd2019的论文分享,本篇是做预算分配的,因为跟我最近做的工作有些关系,所以刚好整理一下。
背景
预算分配核心是解决该把钱投在哪的问题,本篇文章意在提出一种做预算分配的通用框架,包括两个步骤,首先通过历史数据去学习需求曲线,也可称为市场响应模型(market response model),然后基于模型进行优化预算分配。
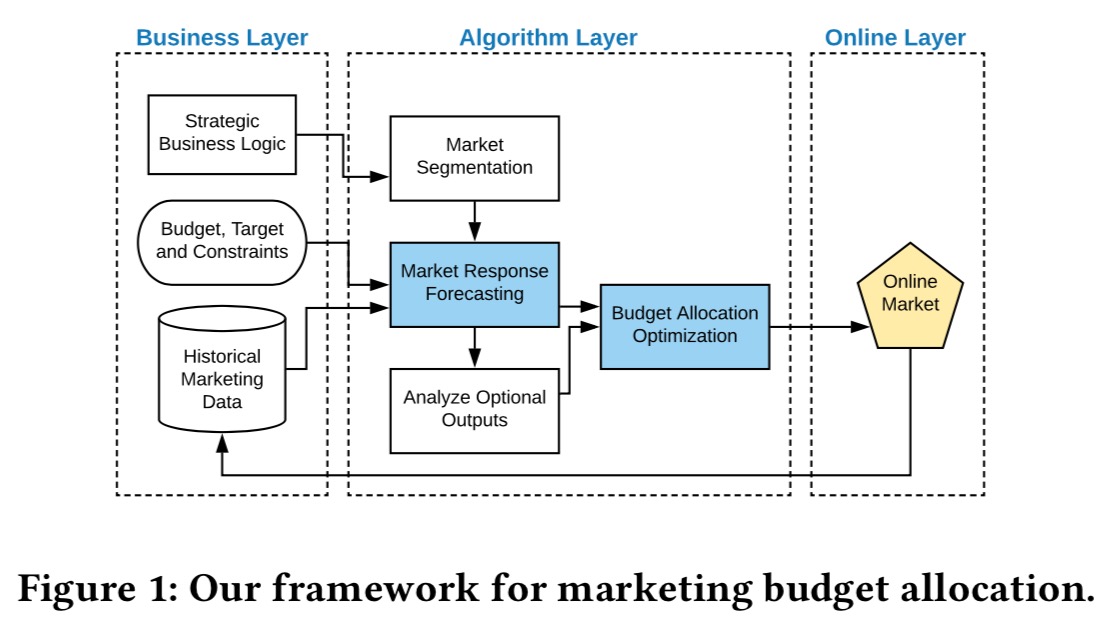
整个市场可以根据不同的商品、客户、消费习惯等维度分为多个组(定价歧视的分组,segment),为了将预算分配给各个组,我们需要根据每个组的预算来预测每个组的销量变化情况。尽管一些黑盒的预测方法,如深度学习,已经广泛应用于一些预测问题,但是这样预测和制定决策之间还有很大的gap,其中一个重要的问题就是很难将黑盒的预测结果转化成分配决策。相反,如logit demand curve有明确的表达形式,并且广泛应用于经济学之中,它的缺点则是智能对于每一个市场分组来拟合,并不能利用不同分组下的通用的信息,这会造成很严重的数据分离的问题,因此文中提出一种半黑盒的预测模型,用神经网络来扩展logit demand curve的能力。预测模型的输入被分成两部分:独立的变量和环境变量(上下文变量)。环境变量是市场本身的属性,比如商品品牌、顾客属性、消费时间等等。同时可以证明market cost(市场对于价格最敏感的点)只跟bias parameter有关,所以可以用相同的神经网络来计算不同segment的bias parameter,而弹性参数可以在拟合数据的时候求出,这样销量和花费的变动关系可以有一个显示的表示。
一旦需求曲线确定了,预算分配则可以表示成一个优化问题。用\(N\)表示segment数量,预算分配需要优化\(N\)个变量,在一定预算约束下最大化销量。由于logit demand cruve是非凸的,所以优化问题也是非凸的,文中提出一种办法可以将该问题转化成等价的凸问题。
同时,这个框架可以兼容多种业务约束,包括花费上限、利润下限、或者roi下限。因为有时候价格需要以99结尾,比如19.99,所以有时候变量需要从一个固定的集合取值,本框架也支持对于离散问题的优化求解,可以将该问题转化成一个多选择的背包问题(MCKP,Multiple Choice Knapsack Problem),近似在\(\mathcal{O}(N)\)的时间复杂度下求解。
市场响应(Market Response)
Logit Response Model
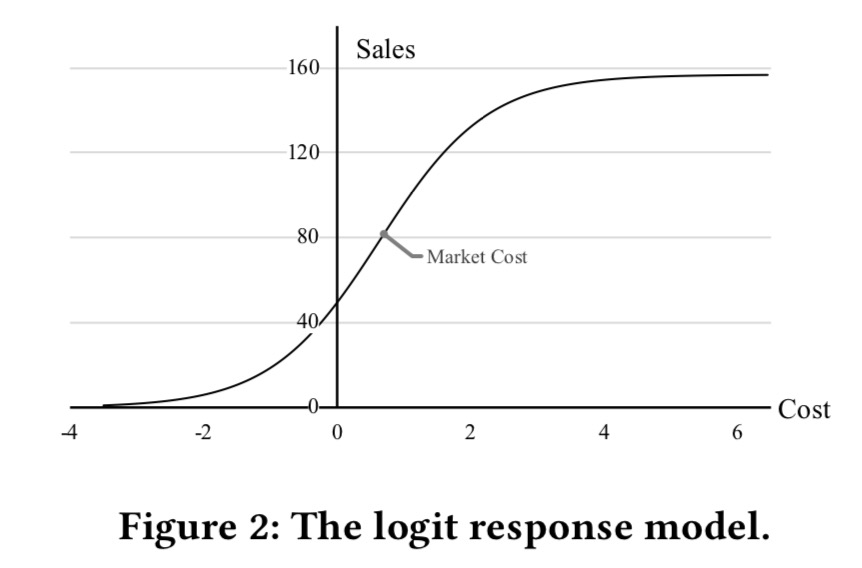
第\(i\)个segment的logit model定义为 \[ d_i(c):=\frac{D_i}{1+\exp{\{-(a_i+b_ic\}}},i=1,\cdots,N \] 其中\(c\)是该市场上的单位花费,\(D_i>0\)表示第\(i\)个segment的全部市场销量,\(c\)既可以大于0也可以小于0,正的花费表示价格折扣,负的花费表示增加附加费。因为每个市场分组都很稳定,所以\(D_i\)可以通过统计的方式得到。\(b_i\)表示敏感度,在一般的情况下,\(b_i>0\)。需求曲线最陡点在\(\hat{c}_i=-a_i/b_i\),我们成这个点为市场花费(market cost),它表示了市场上的平均花费,同时销量在其附近变动时候变化最敏感。随着花费增加,销量会逐渐降低,这是由于边际效应递减。
衡量敏感度的通用方式为弹性,类比价格弹性,我们定义花费弹性为销量变化百分比与花费变化百分比的比值: \[ e_i(c_1,c_2)=\frac{[d_i(c_2)-d_i(c1)]c_1}{[c_2-c_1]d_i(c_1)} \] \(c\)处的弹性可以使得\(c_2\rightarrow c_1\)时取得 \[ e_i(c)=\nabla_cd_i(c)\frac{c}{d_i(c)} \] 根据以上我们可以推 \[ \begin{aligned} \nabla_cd_i(c)=&\frac{D_ib_i\exp{\{-(a_i+b_ic\}}}{[1+\exp{\{-(a_i+b_ic\}}]^2}\\ e_i(c)=&\nabla_cd_i(c)\frac{c}{d_i(c)}\\ =& \frac{D_ib_i\exp{\{-(a_i+b_ic\}}}{[1+\exp{\{-(a_i+b_ic\}}]^2} \cdot \frac{(1+\exp{\{-(a_i+b_ic\}})c}{D_i} \\ =& \frac{b_ic}{1+\exp{\{(a_i+b_ic\}}} \end{aligned} \] 所以当\(\hat{c}_i=-a_i/b_i\)时,\(e_i(\hat{c}_i)=-a_i/2\)
Semi-black-box Model
logit对于数据的使用能力有限,当我们对于每个segment都学习出一个\(a_i\)和\(b_i\),并没有使用segment之间相同的数据,所以认为此处的\(c\)为独立变量,环境变量用\(\mathbf{x}_i\)表示,环境变量对于所有segment是通用的,并不会因为segment不同而改变(此处指的应该是有控制的改变,如对于某个segment人为改变花费,而环境变量contextual variables并不能控制),传统的神经网络可以将\(\mathbf{x}_i\)和\(c\)都作为输入,而logit只能利用\(c\)作为输入。
假设1:弹性是由环境变量决定的。
相比于直接预测最终的销量,我们用神经网络\(e(\mathbf{x}_i)\)来估计market cost处的的弹性,基于\(e(\mathbf{x}_i)\),弹性的信息可以在不同segment间共享,传统的logit model可以扩展成 \[ d_i(c):=\frac{D_i}{1+\exp{\{2e(\mathbf{x}_i)-b_ic\}}} \] 同时利用了神经网络的表达能力,也显式地表示了价格弹性。
\(e(\mathbf{x}_i)\)的参数需要学习,定义市场份额\(q_i(c)\): \[ q_i(c):=\frac{d_i(c)}{D_i}=\frac{1}{1+\exp{\{-(a_i+b_ic)\}}} \] 其中\(a_i=-2e(\mathbf{x}_i)\)。因为\(D_i\)可以从历史数据上统计得到,所以可以构造训练数据\(\{([\mathbf{x_i}, c_1],\hat{q}_{i1}),\cdots,([\mathbf{x_i}, c_{M_i}],\hat{q}_{i{M_i}})\},i=1,\cdots,N\)。参数可以通过梯度下降来最小化负似然函数 \[ \mathcal{J}=-\frac{1}{\sum_{i=1}^NM_i}\sum_{i=1}^N\sum_{j=1}^{M_i}[ \hat{q}_{ij}\log q_{ij}+(1-\hat{q}_{ij})\log (1-q_{ij}) ] \]
预算分配
对于\(N\)个segments,预算分配需要决定每个segment的花费\(c_i\),用\(\mathbf{c}:=[c_1,\cdots,c_N]\),我们的目标是找到一个最优的\(\mathbf{c}\)在预算约束下来最大化总销量, \[ \begin{aligned} \min_\mathbf{c} && -\sum_{i=1}^N d_i(c_i)\\ \text{s.t.} && \sum_i^Nd_i(c_i)\leq B \end{aligned} \] 其中\(B\)表示预算上限,它既可以为正也可以为负,正的表示花费上限约束,负的表示利润下限约束。
因为\(\sum_{i=1}^Nd_i(c_i)c_i=\sum_{i=1}^ND_iq_i(c_i)c_i\)是一个非凸的函数,直接求解过于困难,所以可以把这个问题转换成等价的凸优化问题。因为\(q_i(c_i)\)是一个严格递增的函数(一般情况下\(b_i>0\)),我们可以得到它的反函数 \[ c_i(q_i)=-\frac{a_i}{b_i}-\frac{1}{b_i}[\ln(1-q_i)-\ln q_i], q_i\in(0,1),i=1,\cdots,N \] 定义\(\mathbf{q}:=[q_1,\cdots,q_N]\),约束\(g(\mathbf{q})\)可以表示为 \[ g(\mathbf{q}):=\sum_{i=1}^ND_iq_ic_i(q_i)-B \] 对其求导之后可以发现\(g(\cdot)\)是个凸函数,所以原问题可以写成凸优化问题 \[ \begin{aligned} \min_\mathbf{q} && \sum^N_{i=1} D_iq_i \\ \text{s.t.} && g(\mathbf{q})\leq 0 \end{aligned} \] 通过引入一个对偶变量\(\lambda\),使用拉格朗日乘子法来优化这个问题 \[ \begin{aligned} \mathcal{L}=& -\sum^N_{i=1}D_iq_i + \lambda (\sum^N_{i=1}D_iq_ic_i(q_i)-B) \\ =& \sum^N_{i=1}(\lambda D_iq_ic_i(q_i)-D_iq_i)-\lambda B \end{aligned} \] 根据KKY条件有 \[ \begin{aligned} g(\mathbf{q}^*) \leq &0\\ \lambda^*\geq& 0\\ \lambda^*g(\mathbf{q}^*)=&0\\ \nabla_{q_i}(\lambda^*D_iq_i^*c_i(q_i^*)-D_iq_i^*)=&0\\ i=1,\cdots,N \end{aligned} \] 其中\(\mathbf{q}^*\),\(\lambda^*\)是原问题和对偶问题的最优解。
令\(g(\tilde{q})\)表示表示\(g(\mathbf{q})\)的最小值,对\(g(\mathbf{q})\)求\(q_i\)的偏导,并令其为0: \[ \ln\frac{\tilde{q}_i}{1-\tilde{q}_i} + \frac{\tilde{q}_i}{1-\tilde{q}_i}=a_i-1,i=1,\cdots,N \] 利用Lambert W函数,\(g(\tilde{\mathbf{q}})\)是唯一的 \[ \tilde{\mathbf{q}}_i=\frac{W(\exp(a_i-1))}{W(\exp(a_i-1))+1},i=1,\cdots,N \] 当\(g(\tilde{\mathbf{q}})>0\),无解,当\(g(\tilde{\mathbf{q}})=0\),\(\mathbf{q}^*=\tilde{\mathbf{q}}\),当\(g(\tilde{\mathbf{q}})<0\),则以下假设成立
假设2:存在\(\mathbf{q}\)使得\(g(\mathbf{q})<0\)。
当以上假设成立时,约束函数\(g(\mathbf{q})\)满足Slater’s condition,而KKT条件提供了最优的充分必要条件。
又根据KKT条件有 \[ \begin{aligned} \nabla_{q_i}(\lambda^*D_iq_i^*c_i(q_i^*)-D_iq_i^*)=&0\\ \lambda^*(c_i(q_i^*)+q_i\nabla_{q_i}c_i(q_i^*))=&1\\ \lambda^*(c_i(q_i^*i)+q_i\nabla_{q_i}c_i(q_i^*))=&1\\ \lambda^*( -\frac{a_i}{b_i}-\frac{1}{b_i}[\ln(1-q_i^*)-\ln q_i^*] + q_i^* (-\frac{1}{b_i}[\frac{-1}{1-q_i^*}-\frac{1}{q_i^*}]) )=&1 \\ \lambda^*( -a_i+\ln\frac{q_i^*}{1-q_i^*} + q_i^* ([\frac{1}{1-q_i^*}+\frac{1}{q_i^*}]) )=&b_i \\ \lambda^*( -a_i+\ln\frac{q_i^*}{1-q_i^*} + \frac{1}{1-q_i^*} )=&b_i \\ \lambda^*( -a_i+\ln\frac{q_i^*}{1-q_i^*} + \frac{1-q_i^*+q_i^*}{1-q_i^*} )=&b_i \\ \lambda^*( 1-a_i+\ln\frac{q_i^*}{1-q_i^*} + \frac{q_i^*}{1-q_i^*} )=&b_i \\ \end{aligned} \] 因为\(b_i>0\),所以我们有\(\lambda^*\neq0\)。
定义\(x_i:=\frac{q_i^*}{1-q_i^*}\),带入上式有 \[ \begin{aligned} \ln x_i+x_i=&a_i+\frac{b_i}{\lambda^*}-1\\ x_ie^{x_i}=&\exp(a_i+\frac{b_i}{\lambda^*}-1) \end{aligned} \] 因为等式右边恒大于0,有 \[ x_i=W(\exp(a_i+\frac{b_o}{\lambda^*}-1)) \] 其中\(W(\cdot)\)是Lambert W函数,所以 \[ q_i^*=\frac{x_i}{x_i+1}=\frac{W(\exp(a_i+\frac{b_o}{\lambda^*}-1))}{W(\exp(a_i+\frac{b_o}{\lambda^*}-1))+1} \] 因为\(\lambda^*\neq0\),根据KKT条件,我们有\(g(\mathbf{q}^*)=0\),所以最优性条件为 \[ \begin{aligned} g(\mathbf{q}^*)=&\sum^N_{i=1}D_iq_i^*c_i(q_i^*)-B=0\\ q_i^*=&\frac{W(\exp(a_i+\frac{b_o}{\lambda^*}-1))}{W(\exp(a_i+\frac{b_o}{\lambda^*}-1))+1}, i=1,\cdots,N\\ \lambda^*\geq&0 \end{aligned} \] 可以发现所有原始变量都可以被同一个对偶变量表示出来,定义 \[ q_i(\lambda):=\frac{W(\exp(a_i+\frac{b_o}{\lambda}-1))}{W(\exp(a_i+\frac{b_o}{\lambda}-1))+1},\lambda\in(0,+\infty),i=1,\cdots,N \] 和 \[ \begin{aligned} f(\lambda):=&\sum^N_iD_iq_i(\lambda)\\ g(\lambda):=&g(\mathbf{q}(\lambda)),\lambda \in(0,+\infty) \end{aligned} \] 所以找到使得\(g(\lambda)=0\)的根\(\lambda^*\)就可以得到原问题的最优解\(\mathbf{q}^*=\mathbf{q}(\lambda^*)\)。
通过分别对\(f(\lambda)\)和\(g(\lambda)\)求导,可得两个函数的导数都是恒小于零,所以两个函数严格单调递减,所以可以通过二分法来找到最优解。

总结
文章后面给出了几种扩展以及实验,实验先是利用模拟的数据和离线数据集做了验证,之后在淘票票上做了ab测试,roi有40%的提升。
本篇意在提出一个通用的预算分配的框架,同时为了解决数据分离的问题,引入了神经网络构造了半黑盒的预测模型,在之后优化阶段,通过一些比较好的性质,比如对bias parameter的性质假设,构造了高效、简单的求解算法,避免了预测阶段使用黑盒模型导致优化困难的问题。