这篇文章第一次看见比较早了，当时看着感觉总体思路还不错，就是最后的实验做的不是很solid，所以也没写，最近发现这篇文章中了nips2020，就拿出来写一写。

Introduction

近几年，对treatment effect的关注越来越多，异质处理效应分析，也叫subgroup analysis，用于找到拥有相似协变量和相同的处理反应的子群体，这样可以更好的的解释不同子群体上的处理效应，也能更好的设计未来的实验。

构建一个可信赖的个体处理效应（ITE，Individual Treatment Effect）的估计器对于识别出拥有相似协变量和相近的处理反应的目标是十分重要的，目前较为成熟的HTE分析是在对ITE进行估计的同时，递归划分目标人群（各类树模型）。在这些HTE分析的方法中，它们假设子群体内的处理效应是同质的，采用样本均值作为群体处理效应，划分群体的指标是最大化不同子群体之间的异质性。在这样的设定中，任意一个群体都会被划分成两个字群体，因为不管怎么划分，两个子群体的处理效应都会是有差别的，也就是说这些方法只考虑组间的差异性，却没有考虑到组内的同质性。

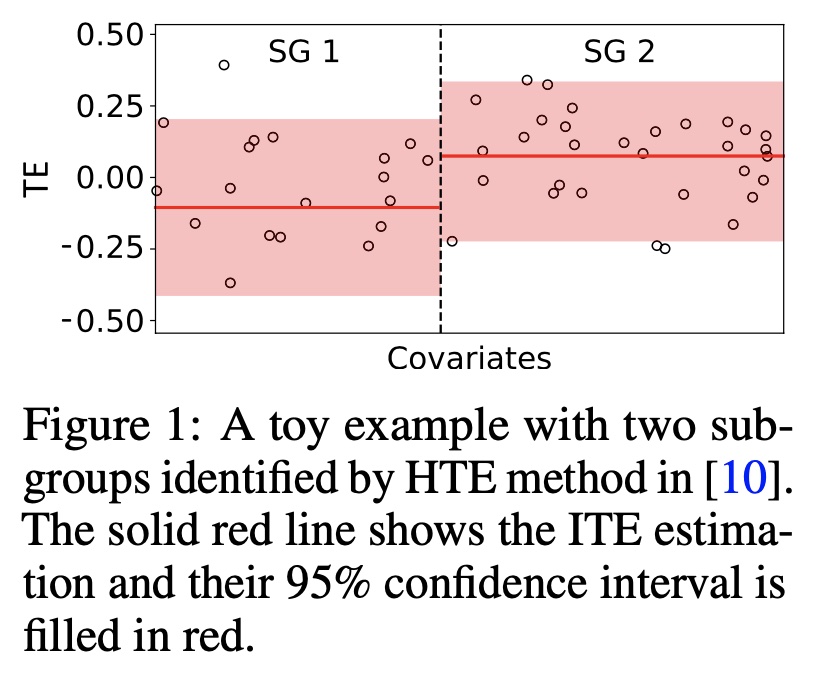
这样只依赖于组间的异质性的划分方式，会导致一些错误的发现。上图中是一个例子，真实的处理效应是一个均值为0标准差为0.1的正态分布，但是采用最大化组间异质性的划分方式，依然是可以划分出两个子组拥有不同的处理效应，这样就产生了一个错误的、虚假的群体划分。基于这样的群体划分做出的决策必然是无效的，甚至更糟糕。

这篇文章提出了一个鲁棒性递归划分（robust recursive partitioning，R2P）方法来避免这种错误的发现，它具有以下特性：

R2P挖掘异质性群体的时候并不依赖于任何特定的ITE估计方法，可以采用各种各样的方式来构造ite的估计，十分灵活。
R2P在保证子群体内的同质性的同时，最大化子群体间的异质性。
R2P相比之前的各种方法，提供了一个相对较窄的置信区间的预测。

Robust Recursive Partitioning with Uncertainty Quantification

考虑一个标准的回归问题，d维协变量\(\cal{X}\in\mathbb{R}^d\)和1维的结果\(\cal{Y}\in\mathbb{R}\)，给定数据集\(\cal{D}=\{(x_i,y_i)\}^n_{i=1}\)，我们假设样本是独立同分布，从\(\cal{X}\times\cal{Y}\)的分布\({\cal{P}}_{X,Y}\)采样得到。我们感兴趣于估计\(\mu(x)=\mathbb{E}[Y|X=x]\)，，\(X=x\)时的条件期望结果。我们把估计器表示为\(\hat{\mu}:\cal{X}\rightarrow\cal{Y}\)，\(\hat{\mu}\)的预测结果为\(\hat{y}=\hat{\mu}(x)\)。为了量化预测的不确定性，我们采用分割共型预测（split conformal regression，SCR，没有找到相关的中文翻译资料，下面缩写为SCR）来构建置信区间\(\hat{\cal{C}}\)。

在SCR中，给定一个覆盖率\(\alpha\in(0,1)\)，我们将数据集\(\cal{D}\)分割为训练集\(\cal{I}_1\)和验证集\(\cal{I}_2\)，互斥且拥有相同的大小，在训练集\(\cal{I}_1\)上训练预测模型\(\hat{\mu}^{\cal{I}_1}\)，然后对\(\cal{I}_2\)上的每个样本计算\(\hat\mu^{\cal{I}_1}\)的残差，对于测试集样本x的置信区间为 \[ \hat{\cal{C}}^{\cal{I}_1,\cal{I}_2}(x)=[\hat{\mu}^{lo}(x),\hat\mu^{up}(x)]=\bigg[\hat{\mu}^{\cal{I}_1}(x)-\hat{Q}^{\cal{I}_2}_{1-\alpha},\hat{\mu}^{\cal{I}_1}(x)+\hat{Q}^{\cal{I}_2}_{1-\alpha}\bigg] \] 其中\(\hat{Q}^{\cal{I}_2}_{1-\alpha}\)定义为残差集合中\(\{|y_i-\hat{\mu}^{\cal{I}_2}(x_i)|\}_{i\in\cal{I}_2}\)的第\((1-\alpha)(1+1/|\cal{I}_2|)\)的分位数。假设训练集和测试集的样本是独立同分布，上面定义的置信区间感满足收敛\(\mathbb{P}\big[y\in \hat{\cal{C}}^{\cal{I}_1,\cal{I}_2}\big]\geq1-\alpha\)。

简单解释一下，假设\(\alpha=0.05\)，给定1000个测试样本，SCR可以产出一个置信区间，使得至少950个样本会存在于置信区间内（我们经常说这样的样本被覆盖了）。然而，这个收敛保证的是整个协变量的空间，当我们在进行子群体分析时候，我们将协变量空间\(X\)分成\(X_1,X_2\)，使得\(X_1\)上存在800个样本，\(X_2\)上存在200个样本，可能\(X_1\)上存在\(790\)个样本被覆盖，\(X_2\)上只有160个样本被覆盖，在这个例子上，\(X_2\)上80%的样本被覆盖，这种情况并不是我们想要的，我们想在任意子人群上都得到相应收敛的置信区间，而不是整体变量空间上，R2P就解决了这个问题。

用\(\Pi\)表示协变量空间\(\cal{X}\)上的一个划分，\(|\Pi|\)为子组的数量，\(l_j\)为\(\Pi\)的元素，\(l(x;\Pi)\)为包含样本x的子组。记\(\cal{D}_l=\{(x_i,y_i)\in\cal{D}|x_i\in l\}\)为子组\(l\)上的样本集合。我们用结果变量的中心化程度来评估子组\(l\)上的同质性，用SCR将样本\(D_l\)分割为\(\cal{I}_1\)和\(\cal{I}_2\)，用\(\hat{\mu}_l(x)\)表示在训练集\(\cal{I}_1\)上的结果变量均值，我们可以在子组\(l\)上构建置信区间\(\hat{\cal{C}}_l(x)\)，其中\(\hat{\mu}^{up}_{l}(x)=\hat{\mu}_l+\hat{Q}^{\cal{I}_2}_{1-\alpha}\)和\(\hat{\mu}^{lo}_{l}(x)=\hat{\mu}_l-\hat{Q}^{\cal{I}_2}_{1-\alpha}\)。为了方便下面去掉样本集的标记\(\cal{I}_1^l\)和\(\cal{I}_2^l\)。子组\(l\)上的平均结果为\(\hat{\mu}_{l,mean}=\mathbb{E}\big[\hat{\mu}_l(x)\big]\)，我们定义子组\(l\)上的期望绝对偏差为\(S_l=\mathbb{E}[v_l(x)]\)，其中 \[ v_l(x)=\big(\hat{\mu}_{l,mean}-\hat{\mu}^{up}_l(x)\big)\mathbb{I}\big[\hat{\mu}_{l,mean}>\hat{\mu}^{up}_l(x)\big] +\big(\hat{\mu}^{lo}_l(x) - \hat{\mu}_{l,mean}\big)\mathbb{I}\big[\hat{\mu}_{l,mean}<\hat{\mu}^{lo}_l(x)\big] \] 当置信区间\(\hat{C}_l(x)=\big[\hat{\mu}_l^{lo}(x),\hat{\mu}_l^{up}(x)\big]\)包含均值\(\hat{\mu}_{l,mean}\)，则\(v_l(x)=0\)。\(v_l(x)\)表征了子组\(l\)上的同质性，同时相比于\(|\hat{\mu}_l(x)-\hat{\mu}_{l,mean}|\)更具有鲁棒性。

然而最小化\(S_l\)并不足够最大化子组的同质性。如果置信区间\(\hat{C}_l(x)\)非常宽，这样也使得\(S_l=\mathbb{E}[v_l(x)]\)为0，为了避免这个问题，当分割协变量时，也要降低置信区间宽度\(W_l=\mathbb{E}\big[|\hat{C}_l(x)|\big]\) \[ \underset{\Pi}{\min} \sum_{l\in\Pi}\lambda W_l + (1-\lambda)S_l \] 其中\(\lambda \in[0,1]\)是平衡\(W_l\)和\(S_l\)的超参数，这个指标称之为Confident Homogeneity。

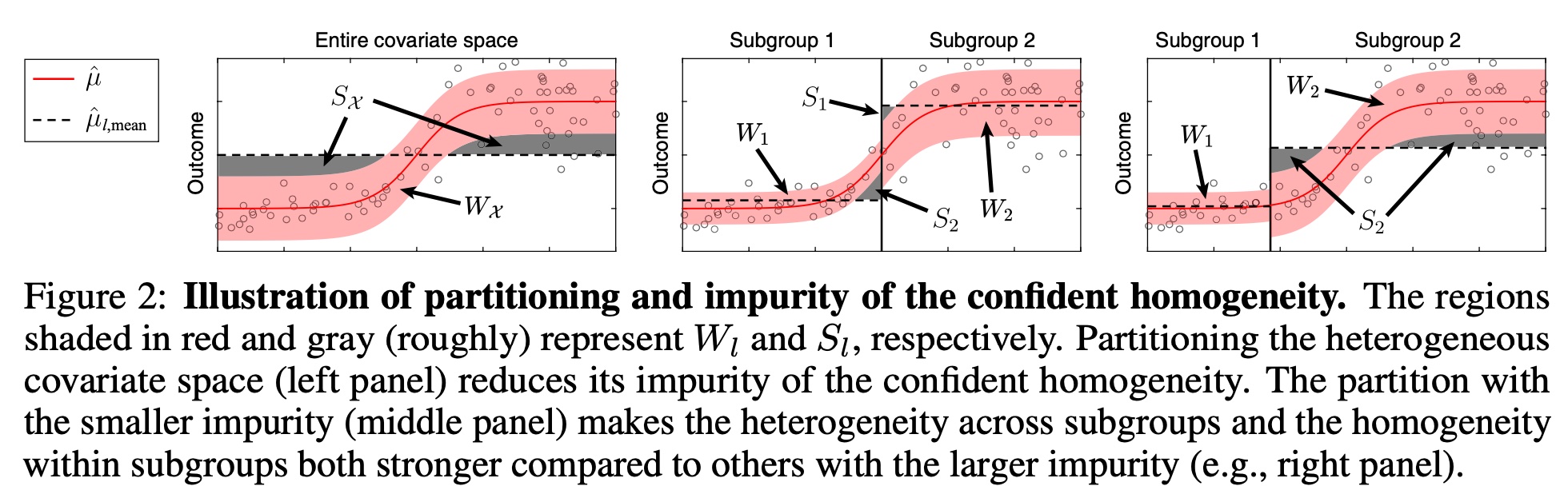
如上图所示，在最小化组内的同质性的同时，最大化组间的异质性。

初始化的时候，定义划分为\(\Pi=\{\cal{X}\}\)，存在使得上述指标更小的划分\(\Pi_c\)，最开始时候我们令\(\Pi_c=\Pi\)，然后用SCR在数据集\(\cal{D}\)上构建置信区间，基于这个置信区间我们计算\(\hat{\cal{W}}_\cal{X}\)和\(\hat{\cal{S}}_\cal{X}\)，即对于任何群体\(l\)我们有\(\hat{\cal{W}}_l=\frac{1}{N_2^l}\sum_{i\in\cal{I}_2^l}|\hat{\cal{C}_l(x_i)|}\)和\(\hat{S}_l=\frac{1}{N_2^l}\sum_{i\in\cal{I}_2^l}v_l(x_i)\)，其中\(N_2^l\)是验证集\(\cal{I}_2^l\)的样本数量。

在初始化之后我们尝试递归划分变量空间，来最小化上面的指标，对于每个群体\(l\)，我们考虑两个互斥相邻的群体\(l_k^+(\phi)=\{x\in l|x_k\geq\phi\}\)和\(l_k^-(\phi)=\{x\in l|x_k<\phi\}\)，其中\(\phi\in(x_k^{l,\min},x_k^{l,\max})\)是划分的阈值，\(x_k\)是第\(k\)维的变量，然后我们分别对两个子集使用SCR构建置信区间，嫁给将样本做如下切割\(\cal{D}_{l_k^+(\phi)}=\cal{I}_1^{l_k^+(\phi)}\cup \cal{I}_2^{l_k^+(\phi)}\)和\(\cal{D}_{l_k^-(\phi)}=\cal{I}_1^{l_k^-(\phi)}\cup \cal{I}_2^{l_k^-(\phi)}\)，在计算残差的时候，我们并不训练新的模型，直接采用上一个节点的预测模型\(\hat\mu_{\cal{X}}\)，这使得组内和组间的预测更具有一致性，同时大大降低了计算开销。利用残差我们可以得到置信区间\(\hat{\cal{C}}_{l_k^+(\phi)}\)和\(\hat{\cal{C}}_{l_k^-(\phi)}\)，然后计算出\(\hat{W}_{l_k^+(\phi)}\)、\(\hat{S}_{l_k^-(\phi)}\)、\(\hat{W}_{l_k^+(\phi)}\)、\(\hat{S}_{l_k^-(\phi)}\)，找到最优化划分变量\(k_l^*\)和阈值\(\phi_l^*\) \[ (k_l^*,\phi_l^*)=\underset{k,\phi}{\arg\min} \quad \lambda \bigg(\hat{W}_{l_k^+(\phi)}+\hat{W}_{l_k^-(\phi)}\bigg) + (1-\lambda)\bigg(\hat{S}_{l_k^+(\phi)}+\hat{S}_{l_k^-(\phi)}\bigg) \] 当满足一定置信度的时候我们进行空间的分割 \[ (1-\gamma)\bigg[\lambda \hat{W}_l + (1-\lambda)\hat{S}_l\bigg] \geq \lambda \hat{W}^*_{l^\pm} + (1-\lambda)\hat{S}_{l^\pm} \] 其中\(\gamma\in[0,1)\)为超参数。通过选择合适的\(\gamma\)参数，可以避免过拟合，同时避免过多、过小的子群体。

具体递归分裂算法如上所示。

Robust Recursive Partitioning for Heterogeneous Treatment Effects

现在我们将R2P应用到HTE估计上，用\(Y_i(1)\)和\(Y_i(0)\)表示潜在结果，0和1分别对应是否施加处理，\(t_i\in\{0,1\}\)，ITE定义为\(\tau(x)=\mathbb{E}\big[Y(1)-Y(0)|X=x\big]\)，我们分别对实验组和对照组拟合模型\(\hat{\mu}^0(x)=\mathbb{E}\big[Y(0)|X=x\big]\)和\(\hat{\mu}^1(x)=\mathbb{E}\big[Y(1)|X=x\big]\)。定义\(\tau(x)\)的\(1-\alpha\)置信区间为 \[ \hat{C}^\tau(x)=[ \hat{\mu}^1(x)-\hat{\mu}^0(X)-\hat{Q}^1_{\sqrt{1-\alpha}}-\hat{Q}^0_{\sqrt{1-\alpha}} ,\quad \hat{\mu}^1(x)-\hat{\mu}^0(X)+\hat{Q}^1_{\sqrt{1-\alpha}}+\hat{Q}^0_{\sqrt{1-\alpha}} ] \] 所以我们可以用相同的方式，来按照HTE进行群体划分。

Experiments

定义几个指标，测试集为\(\cal{D}^{te}\)，群组\(l\)，则群组上的均值和方差为\(\text{Mean}(\cal{D}_l^{te})\)和\(\text{Var}(\cal{D}_l^{te})\)，定义组间的异质性为所有组处理效应均值的期望\(V^{across}=\text{Var}(\{\text{Mean}({\cal{D}}_l^{te}\}_{l=1}^L)\)，其中\(L\)为组数，定义组的平均方差为\(V^{in}=\frac{1}{L}\sum_{l=1}^L\text{Var}({\cal{D}}_l^{te})\)，其中前者用于衡量组间异质性，后者用于衡量组间的同质性

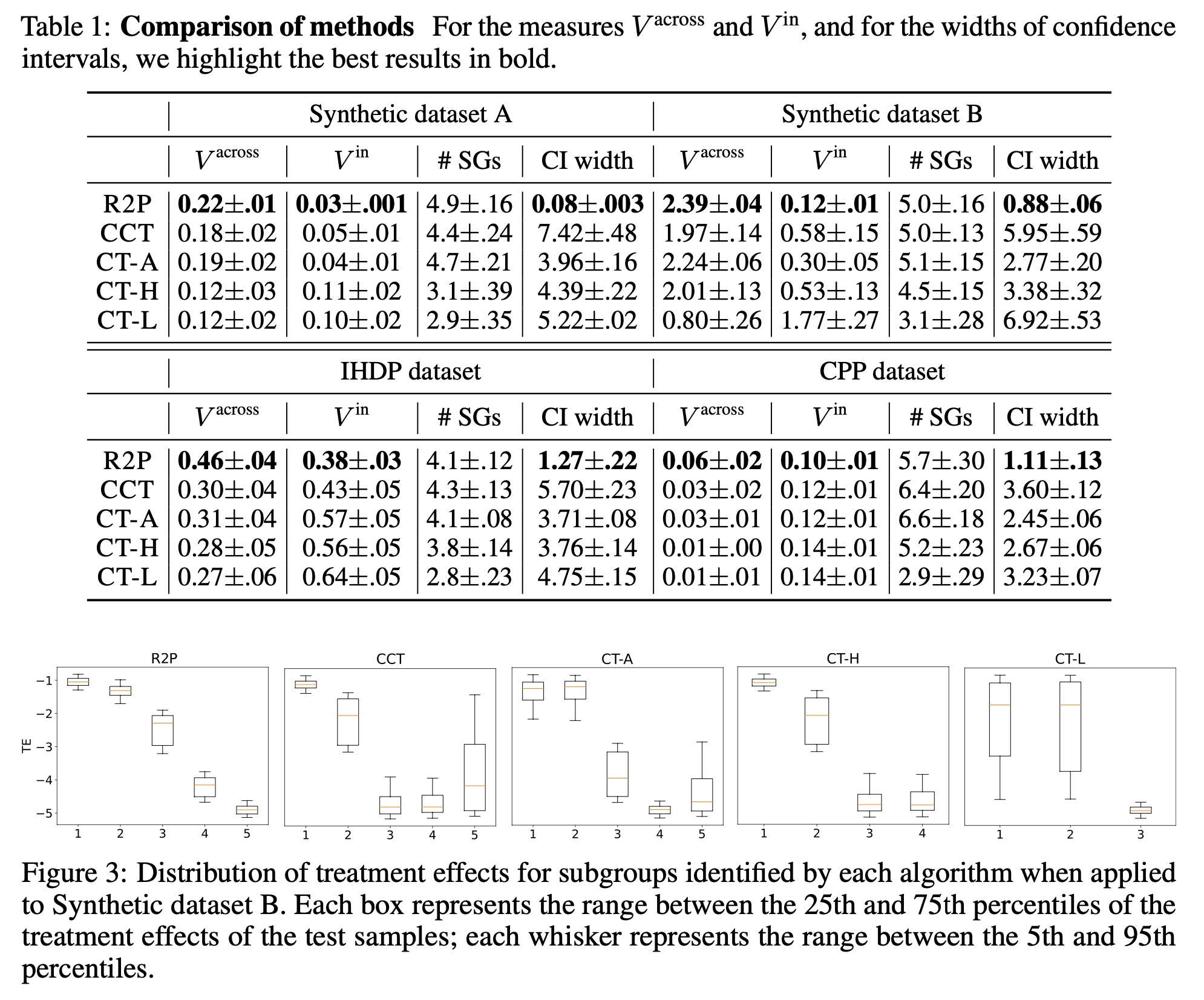
有上图可以看到，R2P在多个数据集上都有较低的组内方差、较高的组间房差，同时置信区间最窄，这也是得益于组内方差较小。同时下面的图是在某个数据集上的分组情况，可以看见R2P产出的分组重叠现象更小，得到的异质群体更有意义。