之前承诺朋友写一些入门的东西,刚好趁这个机会对某些方向进行一些系统化的梳理。这次主要是Brady Neal的 Introduction to Causal Inference(ICI)的课程笔记的翻译和精讲,完整课程链接奉上,同时也希望越来越多的人关注这个方向。
目录:
- 因果推断简介
- 辛普森悖论
- 相关性非因果性
- 潜在结果
- 因果图
因果推断简介
辛普森悖论(Simpson's Paradox)
想象这样一种场景,以后存在某种病毒,Covid-27,在人类中传播,我们对此有两种干预治疗方案(treatment,之后称之为处理),treatment A和treatment B。施加治疗方案B相比于A较少,实施的比例大概是73%和27%,现在由你来决定,为了尽量降低人群死亡率,我们到底该采用哪种治疗方案。
目前你拥有之前患过Covid-27的人的治疗数据,你知道状态的人受到了怎样的治疗方案,病人的状态是一个二元的变量,重症(Severe)或者是轻症(Mild),在这份数据中,大概16%的人采用治疗方案A之后死亡,19%的人采用治疗方案B之后死亡,总的来看仿佛是治疗方案A会有更低的死亡率,但是当我们对不同状态下的病人分别统计的时候,我们会得到相反的结论,在轻症患者中,15%的人在接受治疗方案A之后死亡,10%的人在接受治疗方案B之后死亡,重症患者中,30%的人在接受治疗方案A之后死亡,20%的人在接受治疗方案B之后死亡。
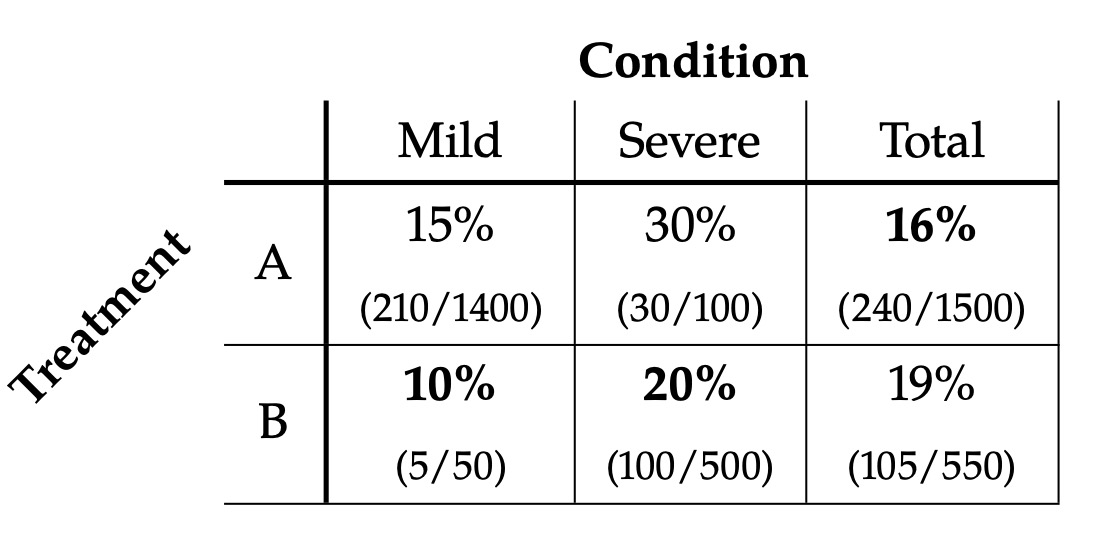
由此产生了一个悖论,我们分不同条件下看时候,治疗方案A的死亡率都高于治疗方案B的死亡率,但是总体看数据时候,我们发现治疗方案A的死亡率会低于治疗方案B的死亡率。这个时候你到底该如何选择呢?
选择治疗方案A或者B都会是正确答案,这取决于数据中的因果结构,换句话说,因果关系是解决辛普森悖论的关键。以下两种场景下,我们可以简单看一下是什么时候该选择治疗方案A什么时候选择治疗方案B。
场景1
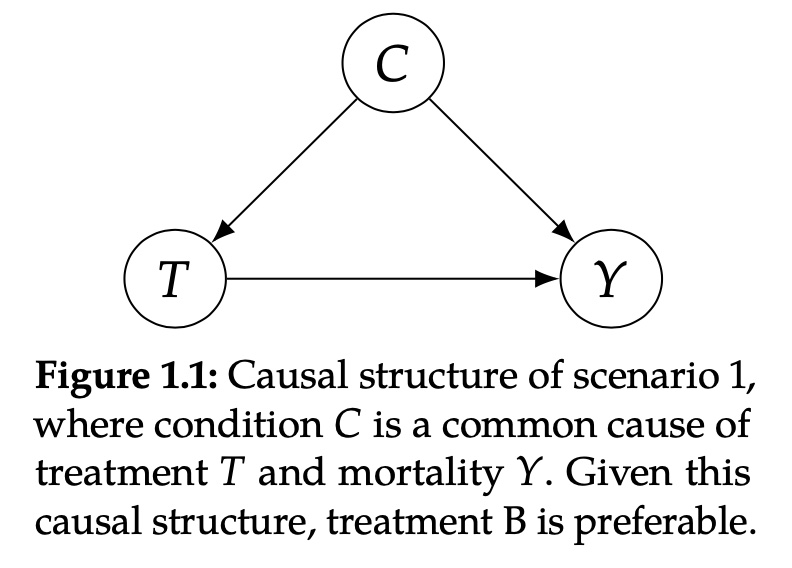
当条件C是处理T的因(cause)时,治疗方案B时更加有效的降低死亡率Y的方案。
举个例子,医生会决定对大部分轻症的患者采用治疗方案A,同时对重症患者更多地采用治疗方案B,因为重症患者的死亡率会更高,病人的症状会决定最后的死亡率\(C\rightarrow Y\),同时重症的状态也使得这个病人更容易被采用治疗方案B,\(C\rightarrow T\),所以最后造成治疗方案B在全体人群上会有更高的死亡率。换句话说,治疗方案B拥有更高的死亡率仅仅是因为病人的状态同时是受哪种治疗方案和死亡率的原因,为了纠正这样的混淆,我们必须在相同的条件下检验T和Y的关系,所以对于这样的场景,我们应你该选择的治疗方案B。
场景2
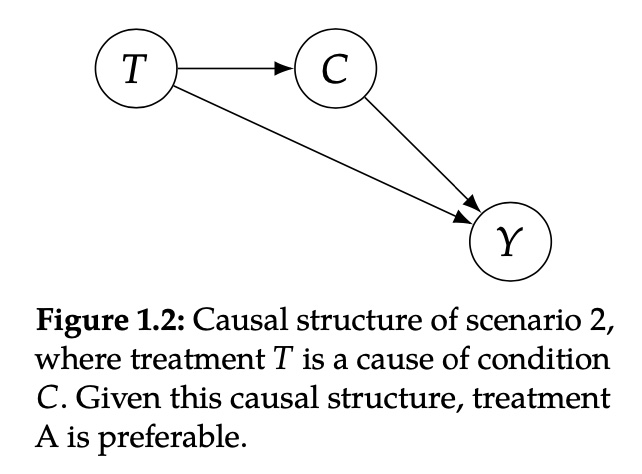
当我们的处理T时条件C的因的时候,治疗方案A则更加有效。比如当治疗方案B有较长的等待周期,病人在接受治疗方案B时需要等待更长的时间,而治疗方案A没有这样的问题。因为患有Covid-27的病人的病情会随时间恶化,所以治疗方案B会使得更多的病人从轻症患者变成重症患者,从而造成了更高的死亡率。因此,即使治疗方案B相比于治疗方案A更有效,\(T\rightarrow Y\),因为处理效应B造成了更坏的状态(重症患者更多),\(T\rightarrow C\rightarrow Y\),总的来说治疗方案B是低效的。(这种场景下,采用哪种治疗方案和病人的状态是相互独立的)
相关性并不意味着因果性
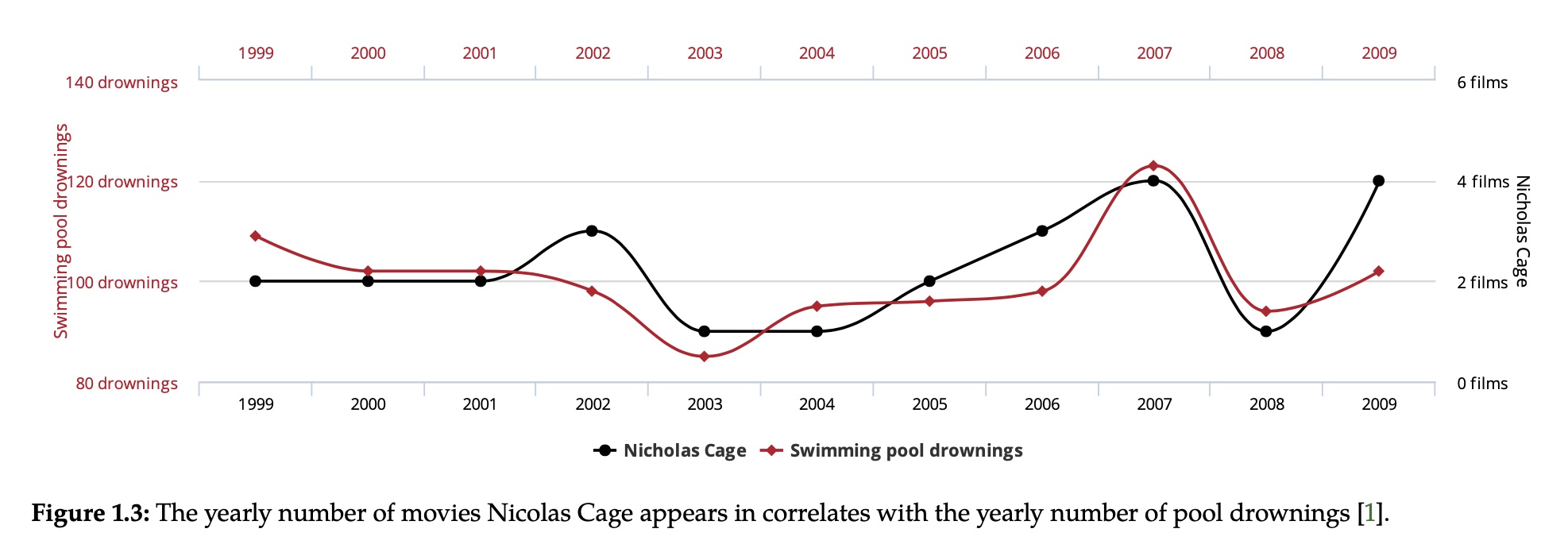
上图中的红线是每年溺死在游泳池中的人数统计,黑线似乎尼古拉斯凯奇的电影数量,我们可以发现两条线之间有很强的相关性,但他们之间真的具有因果性吗?答案肯定是否定的,他们之间的相关性是虚假的,毫无因果关系。
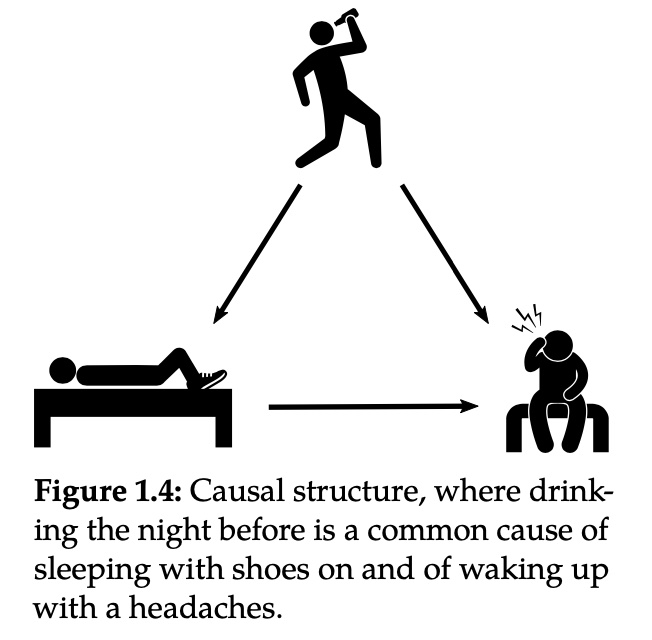
举个例子,大概率下,当你穿着鞋子睡觉,第二天起来会发现头痛,不穿着鞋子睡觉,第二天起来并不会头痛,通常这样的现象并不会被解释成穿鞋睡觉会导致头痛,特别是存在一些原因导致大家穿鞋子睡觉,我们可以认为穿着鞋子睡觉和第二天头痛之间存在关系,但并不是穿着鞋子睡觉造成了头痛,它们可能是由一个共同的原因所导致,比如说宿醉,这样的变量被称之为混淆变量(confounder)。
潜在结果
在本节会阐述一些简单的因果相关的术语和概念。
我们用T表示处理效应,Y表示最后感兴趣的结果变量,X表示协变量,大写字母表示随机变量,小写字母表示该随机变量的取值。大部分情形下我们先考虑T是二元变量,后续我们会讲解多元和连续的情况。
潜在结果\(Y(t)\)表示当一个实验单元(unit)被施加处理(treatment,干预)\(t\)时的结果(outcome),潜在结果可以从观测结果\(Y\)中得到,但并不是所有潜在结果都可以被观测到,因为每次我们只能受到一个处理的影响,所以依赖于施加在实验单元上的处理\(T\)是什么。我们定义第\(i\)个实验单元的个体处理效应(ITE,individual treatment effect)为 \[ \tau_i=Y_i(1)-Y_i(0) \] 无法观测到给定实验单元的所有潜在结果,是因果推断的本质问题。因为我们每次无法同时观测到\(Y_i(1)\)和\(Y_i(0)\),所以我们无法得知每个单元的因果效应\(Y_i(1)-Y_i(0)\)。相比于机器学习,我们只用关心预测观测到的结果\(Y\)。
虽然我们无法得到个体处理效应,但是我们可以计算平均处理效应(ATE,average treatment effect): \[ \tau=\mathbb{E}[Y_i(1)-Y_i(0)]=\mathbb{E}[Y(1) - Y(0)] \] 那么我们如何计算ATE呢,一个简单的做法是直接将两个期望相减\(\mathbb{E}[Y|T=1]-\mathbb{E}[Y|T=0]\),但是实际上很多时候\(\mathbb{E}[Y|T=1]-\mathbb{E}[Y|T=0]\neq \mathbb{E}[Y(1)]-\mathbb{E}[Y(0)]\),前者是一个相关关系,而后者是一个因果关系,它们之间不想等就是因为存在混淆(confounding)。
那么什么情况下,我们可以用两个期望直接相减得到ATE呢?答案是满足ignorability,假设ignorability就像是可以忽略人群差异,随机选择治疗方案,即X对T不影响
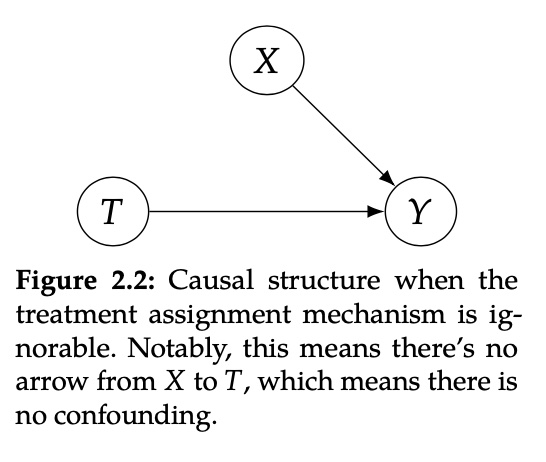
公式化Ignorability(也叫Exchangeability)为 \[ \bigg(Y(1),Y(0)\bigg) \perp T \] 当满足Ignorability时, \[ \begin{aligned} \mathbb{E}[Y(1)] - \mathbb{E}[Y(0)] &= \mathbb{E}[Y(1)|T=1] - \mathbb{E}[Y(0)|T=0] \\ &= \mathbb{E}[Y|T=1] - \mathbb{E}[Y|T=0] \end{aligned} \]
在观测数据中,一般很难满足Ignorability的假设,即我们很难假设各个组下的变量分布无差异,但是如果我们控制某些变量,在某个条件下,子群体间可能会是exchangeable,所以我们定义Conditional Exchangeability或者也叫Unconfoundedness为 \[ \bigg(Y(1),Y(0)\bigg) \perp T \quad \big| \quad X \] 当我们施加干预和潜在结果,在整体上由于存在混淆是有联系的,但是在某个X的分层下,他们并没有联系,换句话说,在控制住X下,使得混淆不存在了,满足了Ignorability。 $$ \[\begin{aligned} \mathbb{E}[Y(1) - Y(0)] &=\mathbb{E}_X\Big[ \mathbb{E}\big[Y(1)-Y(0)|X\big] \Big]\\ &= \mathbb{E}_X\Big[ \mathbb{E}\big[Y|T=1,X\big] - \mathbb{E}\big[Y|T=0,X\big] \Big] \end{aligned}\]$$ ATE为所有X上取边际X上ATE的期望。通常来说,最好的做法就是观测并拟合尽量多的特征在X中,来保证unconfoundedness。
当我们加入更多的特征来实现unconfoundedness,我们也需要考虑另一个假设positivity。Positivity(Overlap, common support)是在任意群体的上,都会有一定概率受到处理 \[ 0 < P(T=1|X=x) <1 \quad \forall x \] 这个假设也很重要,如果\(P(T=1|X=x)=0\)或者\(P(T=0|X=x)=0\),都会使得我们无法计算ATE。
在上述几个假设外,还有几个比较重要的:
- No interference,结果不受到其它干预的影响,\(Y_i(t1,\cdots,t_i,\cdots,t_n)=Y_i(t_i)\)
- Consistency,观测到的结果和潜在结果一致,\(T=t \implies Y=Y(t)\)
- SUTVA,stable unit-treatment value assumption,如果一个实验单元的结果是受到干预的函数,即consistency和no interference的结合。
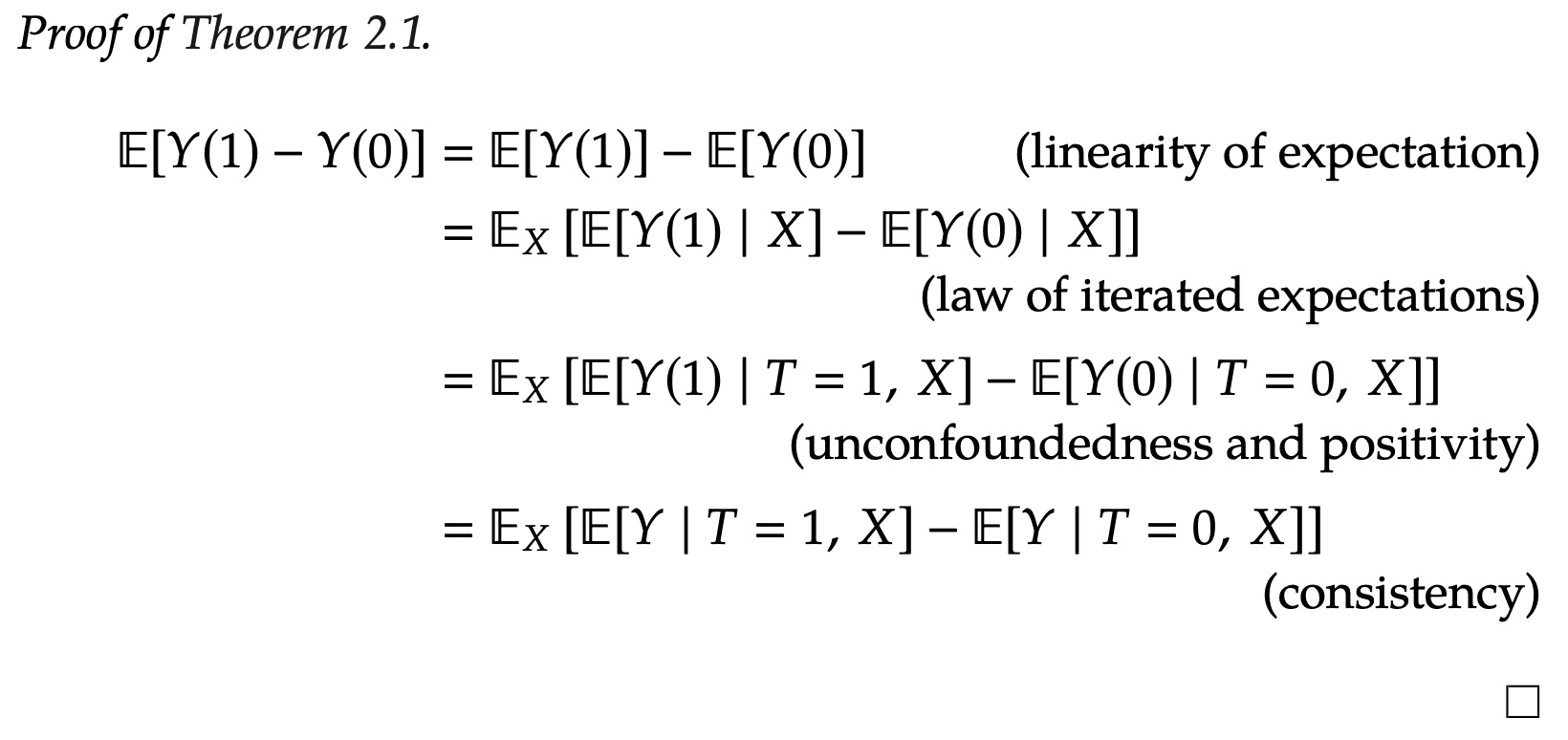
上面的证明讲了满足以上的假设之后,我们怎么计算ATE。
因果图
Graph Terminology
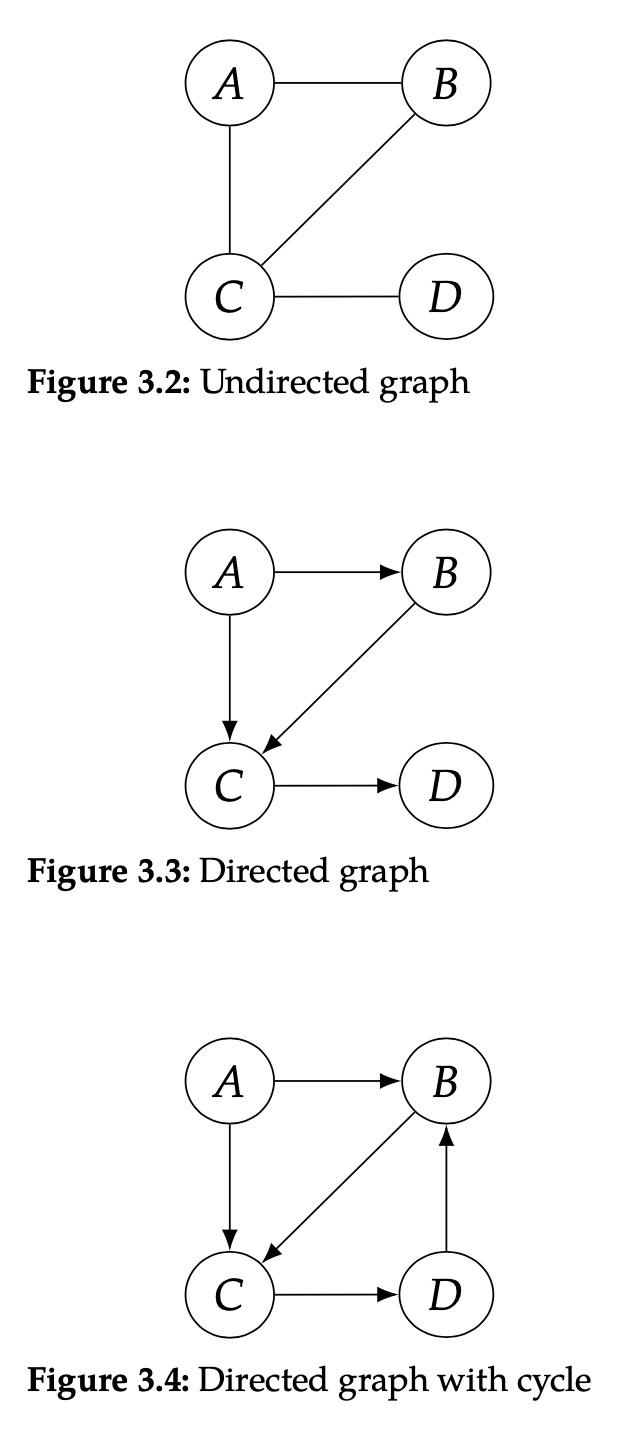
- 图,graph:一系列节点的集合
- 无项图,undirected graph,节点间的连线无方向
- 有项图,directed graph,节点间的连线有方向
- 父节点,子节点
- 近邻,adjacent,两个节点被一条边相连,则两个节点为近邻
- 路径,path,一系列近邻的节点(无需方向)
- 有向路径,direct path,一系列有向节点
- 有向路径的从节点X出发,到节点Y结束,X是Y的祖先,ancestor,Y是X的后代descendant
- 有向无环图,directed acyclic graph (DAG)
Bayesian Networks
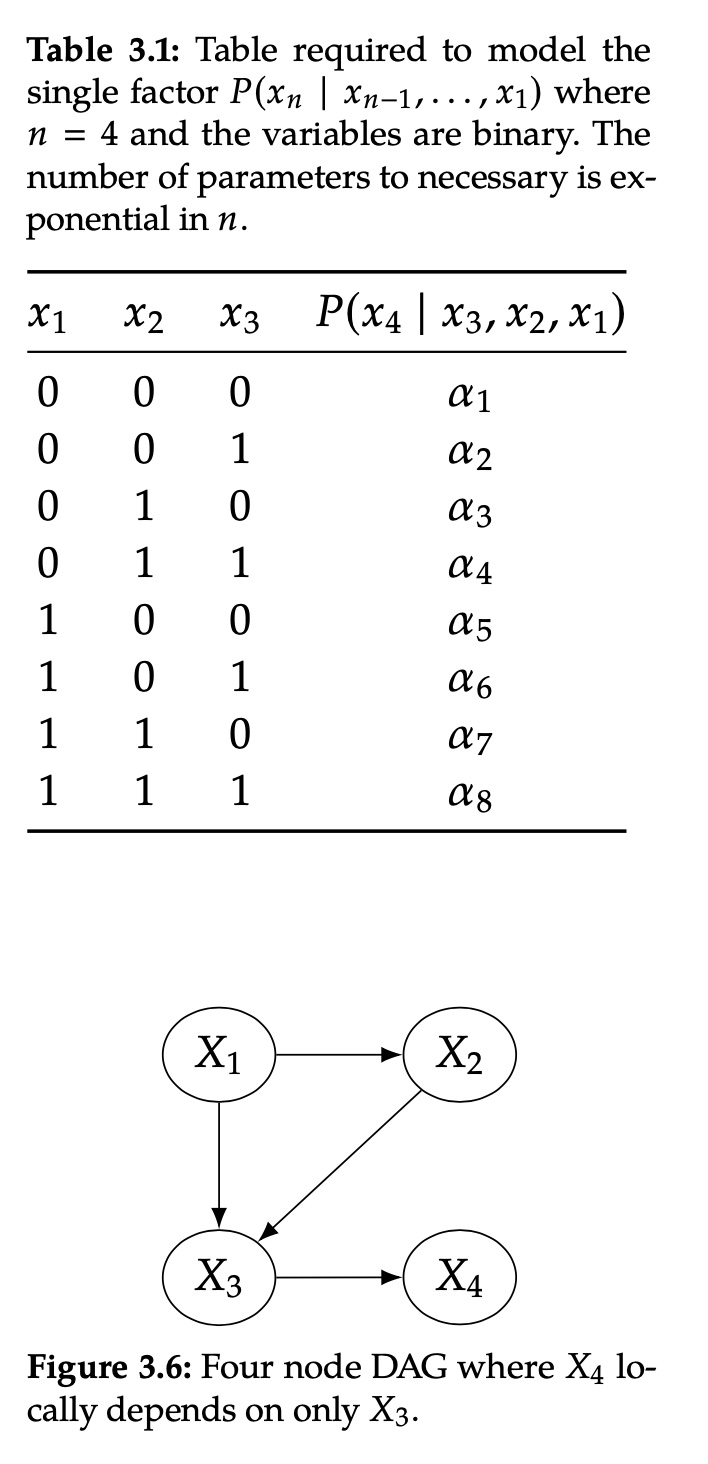
上图的关系,可以用联合分布表示 \[ \begin{aligned} P(x_1,x_2,x_3,x_4) &= P(x_1)P(x_2|x_1)P(x_3|x_2,x_1)P(x_4|x_3,x_2,x_1) \\ &=P(x_1)P(x_2|x_1)P(x_3|x_2,x_1)P(x_4|x_3) \end{aligned} \]
Causal Graphs
“因”的定义(cause),如果变量Y随着变量X的改变而变化,那么就说变量X是变量Y的因。
(Strict) Causal Edges Assumption,在一个有向图中,每一个父节点都是它全部子节点的因。
Two-Node Graphs and Graphical Building Blocks
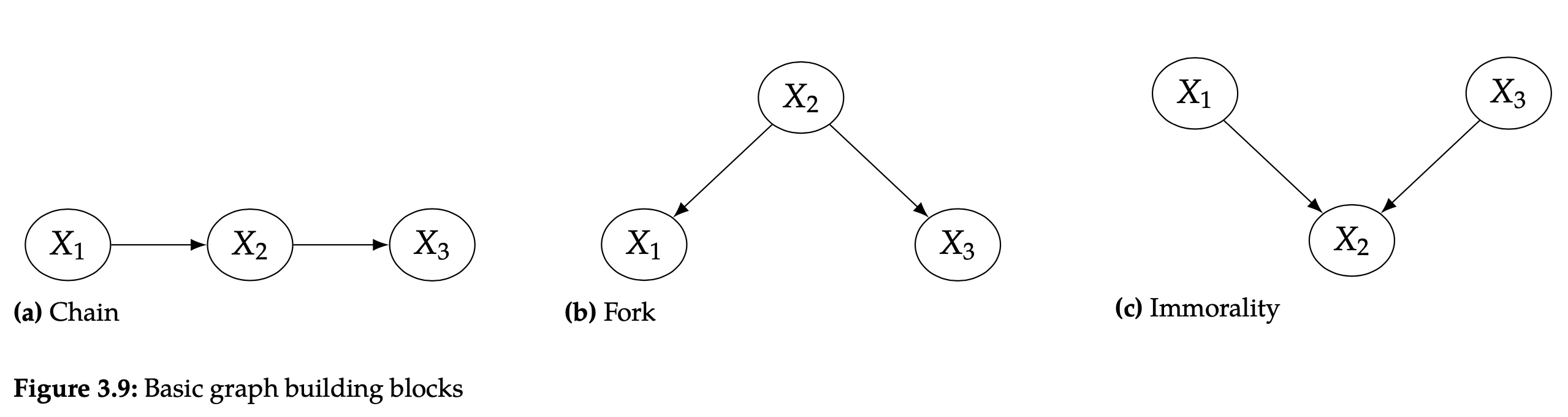
上面简述了三种节点关系,chain、fork和immorality。
如果节点A和B是条件独立的,那么给定节点C,有\(\mathbb{P}(a,b|c)=\mathbb{P}(a|c)\cdot\mathbb{P}(b|c)\),两个独立的节点在图中,是没有线相连的。相反,如果两个节点中存在一条边,这两个节点就是有关联的。
Chains and Forks
在chain中,X1和X3是非依赖的,因为X1造成了X2的改变,同时X2造成了X3的改变。
在fork中,X1和X3是依赖的,因为X2同时决定了X1和X3,
chain和fork都有相同的独立集(set of independencies),如果我们condition在X2上,它都使得X1和X3之间的联系被block住。