这篇文章是airbnb中的2020的kdd,讲的是在之前的dl的探索之后的改进,也是一篇实战性非常强的文章,基础背景,Applying Deep Learning To Airbnb Search。
Optimizing The Architecture
在最开始对DL模型进行迭代的时候,我们也是从增加数据、增加网络深度来优化模型,但是却没什么收益,为了解释增加网络深度为什么对于最后结果没有提升,也尝试了很多做dl的想法,比如residual learning、batch normalization等等。但是这些技巧对于CNN比较适用,并不适合于所有DNN,对于我们这种全链接网络,两层结构的模型对于我们的场景足够了。
如果说更深并不是我们网络结构正确的探索方向,所以我们探索了一些增加能够更加刻画query和listing交互的网络结构,比如deep&wide,attention等等,最终结果也并没有提升。
很多成功的网络结构在我们的场景中,最后都没有起到什么作用,模型结构的收益来自于模型所对比的baseline的缺点,由于网络的不可解释性,我们很难推断出这样的网络结构解决了什么问题,同时我们也很难确定我们的场景中是否存在这样的问题。
为了改进这一现状,我们放弃了读paper->实现模型->线上AB测试的循环,而是遵循用户第一原则,用模型解决用户问题(users lead, model follows)。
Users Lead, Model Follows
在之前的NN模型中,我们发现最后的排序结果并不仅仅带来预定量的提升,同时也降低了搜索结果的平均价格,这表示模型更贴合用户的价格便好。我们怀疑,即使当前价格降低了,当仍有一定空间,为了量化这个空间有多大,我们画出来搜索结果listing价格的中位数和用户最终预定listing的价格的关系图,发现是一个有偏的分布,这说明我们的搜索结果还可以进一步优化。
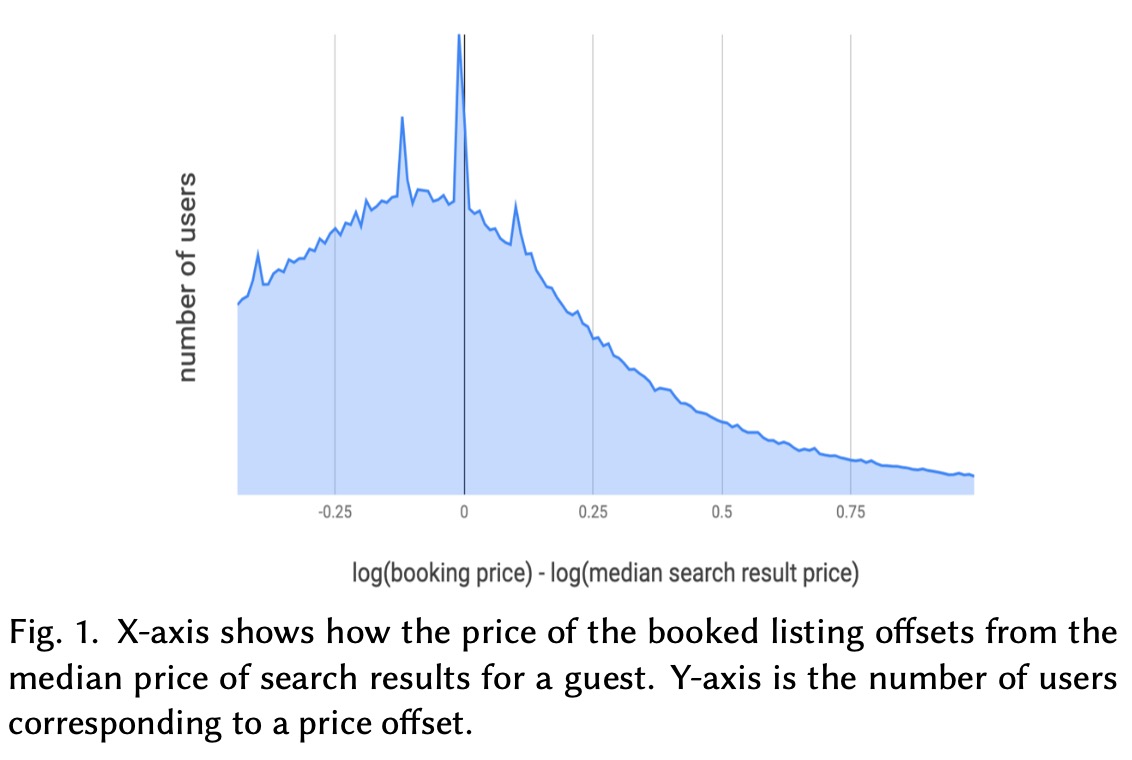
我们的期望是预定价格是搜索结果价格的中位数,整体分布是一个0均值的标准化的分布。这就是一个我们改进的方向,用户更偏好低价的listing,便宜的listing更应该排在前面。
Enforcing Cheaper Is Better
为了增加价格的可解释性,我们对网络结构做了以下改进:
- 将价格从特征中移除,我们将修改后的DNN表示为\(\text{DNN}_\theta(u,q,l_\text{no_price})\)
- 模型最终的结果表示为\(\text{DNN}_\theta(u,q,l_\text{no_price})-\tanh(w\cdot \cal{P} + b)\),其中\(\cal{P}=\log(\frac{1+\text{price}}{1+\text{price}_\text{medium}})\),其中价格中位数为一个常量
上线之后我们发现搜索结果的平均价格降低了5.7%,但是预定量降低了1.5%,我们在分析在线和离线的NDCG之后,认为是价格与其他特征都有比较重的交互,孤立出价格特征会使得模型欠拟合。
Generalized Monotonicity
采用Lattice networks的方式来维持单调性
- \(\cal{P}\)作为特征加入DNDN
- 在输入层,与\(\cal{P}\)相关的权重用二次方,同时符号为负
- 在第二层的隐藏层,部分权重采用二次方,部分权重不变
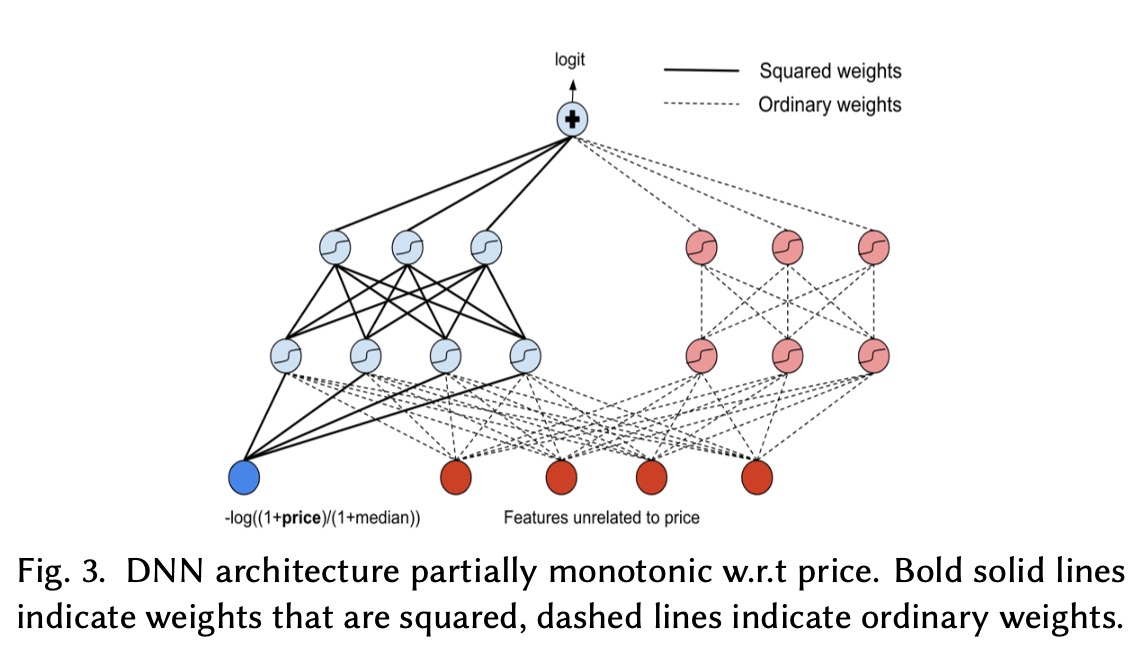
最终线上结果,预定下降了1.6%,对此我们认为因为这样的单调性约束过于严格导致模型拟合的不好。
Soft Monotonicity
经过上面几次尝试,我们觉得DNN,对于给定问题往往可以得到一个合理的解决方案,但是如果是制定某些方向,却会出现非常糟糕的结果。所以在之后的尝试中,我们想通过设置某些context的方式来优化DNN,我们尝试增加一个软的约束来表示越便宜越好,具体的做法就是在loss中增加一部分,来判断两个listing哪个是价格低、哪个是价格高的,通过超参数来控制。
为了测试这个优化点,我们尝试调整超参数,使得线下的NDCG指标与baseline模型一致,这样做是因为我们希望在不损失相关性的前提下,测试低价更好这个改动的影响。
在线上测试中,平均价格下降了3.3%,预定下降了0.67%。在离线分析中我们发现,这是由于我们的评估集中于re-ranking历史log中的头部展示的结果,但是在线上测试中,新的模型是用于当前所有空闲的listing上,导致线上和线下的模型的效果不一致。
Putting Some ICE
为了搞清楚为什么新模型效果不好,我们尝试去分析baseline模型是如何利用价格特征的。我们借鉴了ICE分析(individual conditional expectation),从一次搜索中拿出listing,交互价格同时保证其他特征不变,然后看一下模型的score结果,如下图所示
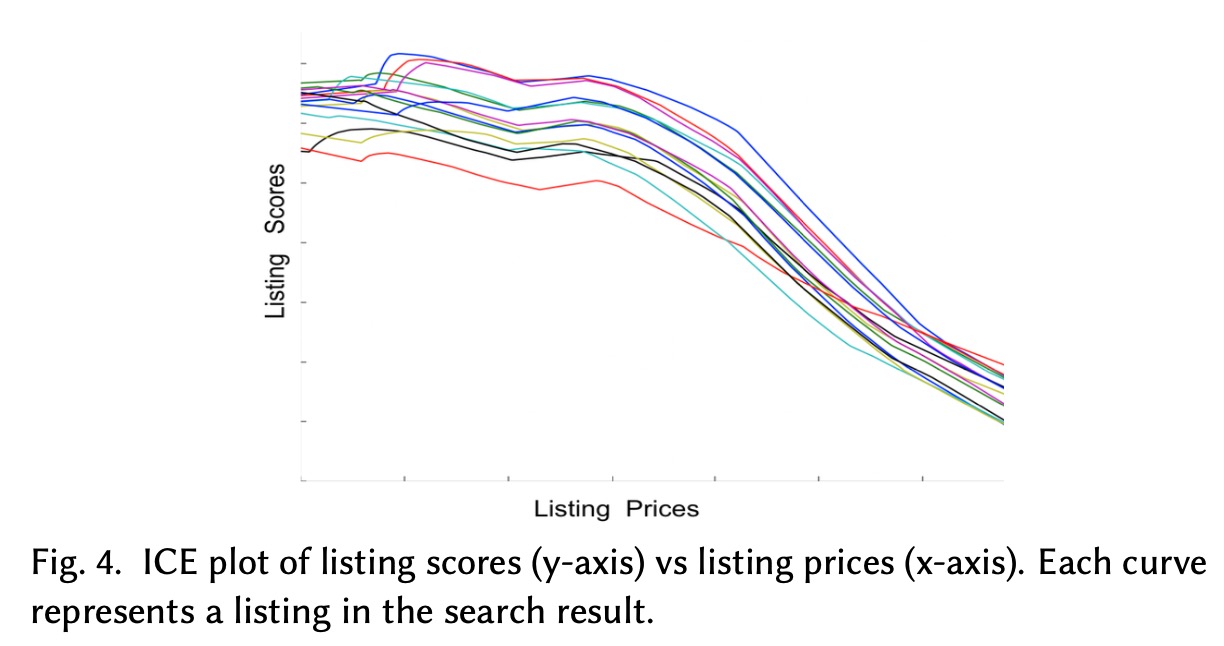
从上图可以看出,模型已经理解了越便宜越好这一点,之前几次压低价格的尝试,这些结构对于搜索质量都有一定降低。
Two Tower Architecture
我们继续回到对于数据的分析上,当我们比较顾客不同搜索结果的价格中位数时,我们发现不同城市会有截然不同的结论,且容易发生于一些长尾的发展中城市上,下图展示了城市上搜索结果中位数价格和预定价格的差异:
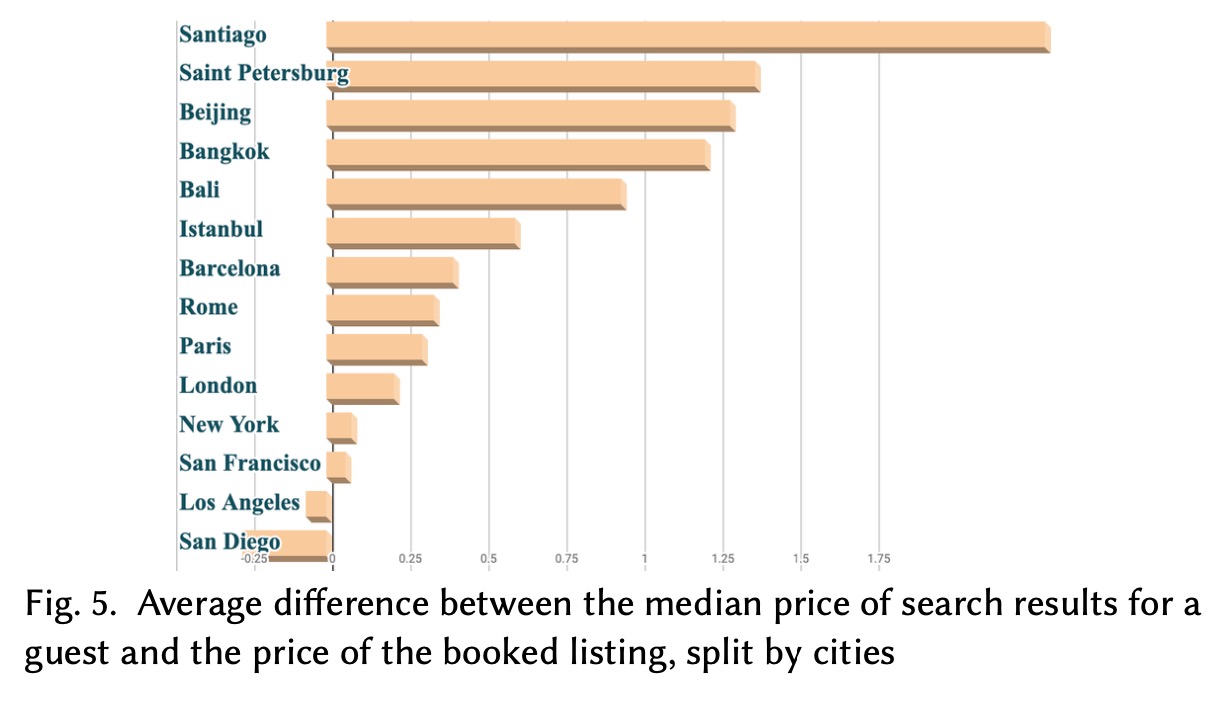
我们认为这样是因为模型在头部的城市上过拟合了,长尾搜上模型泛化能力较差,模型在这些局部条件上学的不太好。
从喂给DNN的特征上,也印证了这一假设,模型是通过pairwise loss来学习,特征的差异只是两个listing的差异,query的特征却是相同的,对最终的结果影响较小。
所以我们对此新的思考是,模型已经学到了越便宜越好的思想,但是并没有对于不同的搜索学到一个正确的价格,所以我们开始更加关注query的特征。
之后第四次的迭代,我们采用了一个双塔的结构,第一个塔的输入是query和user的特征,最终产出100维的向量,第二个塔用listing的特征学一个100维的响亮,然后用这两个向量的欧式距离来衡量query和listing的相关性。
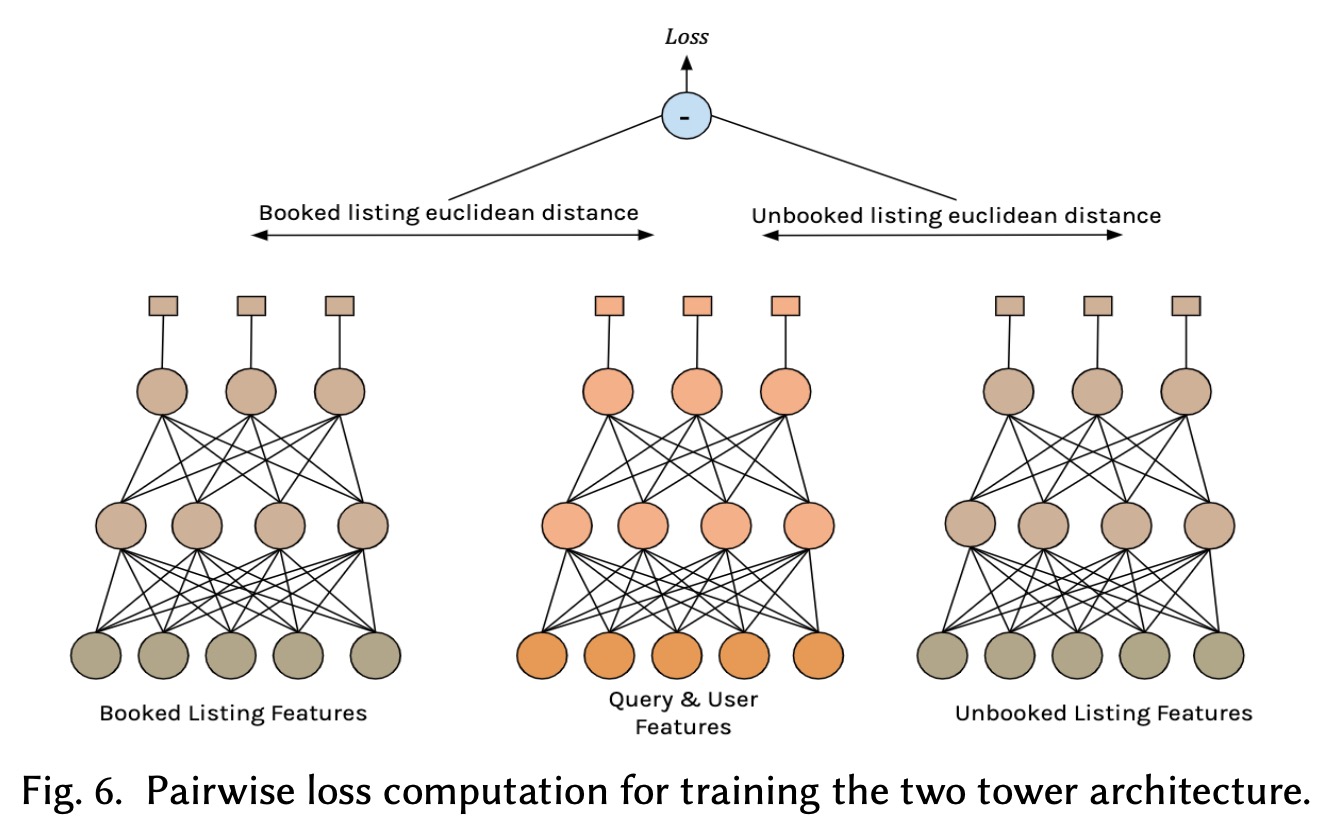
Test Results
线上AB实验之后,预定涨了0.6%,NDCG增加了0.7%,同时搜索结果平均价格降低了2.3%,收益增加0.75%。
除了有结果上的收益,线上预测的响应时间也缩短了,之前的网络结构第一层网络计算复杂度为\(O(N\cdot H\cdot(Q+L))\),其中\(Q\)是query特征数,\(L\)是房间特征数,\(H\)是节点数量,\(N\)为需要预测次数,现在双塔结构,第一层的计算复杂度为\(O(N\cdot H_l \cdot L+H_q\cdot Q)\)。
Architecture Retrospective
即使上线实验取得了收益,我们还是对DNN为何有收益有所顾虑。对此又继续采用ICE plots来看价格变化对于最后结果的影响
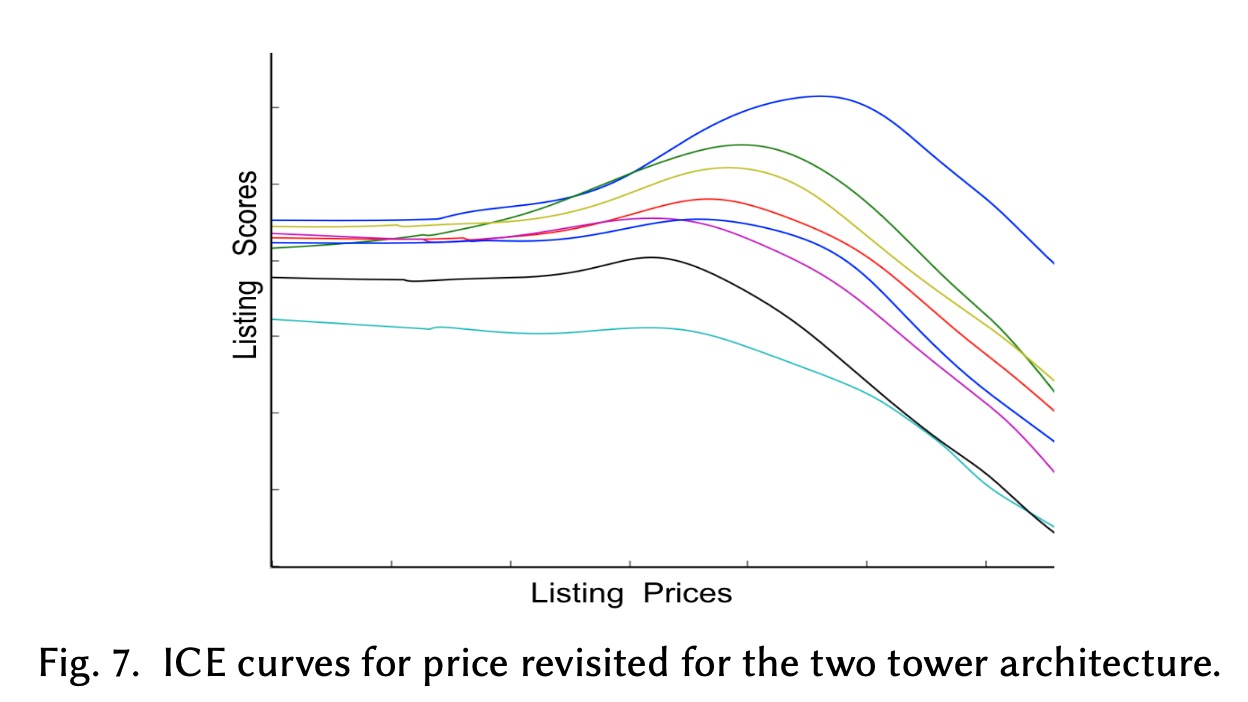
我们发现曲线并不是单调降低,而是在一定位置保持平稳,然后升高再降低,这说明我们的模型找了一个相对合理的价格,同时保持了越便宜越好的特性。
为了进一步了解模型,我们又对模型产出的100维向量做了t-SNE可视化
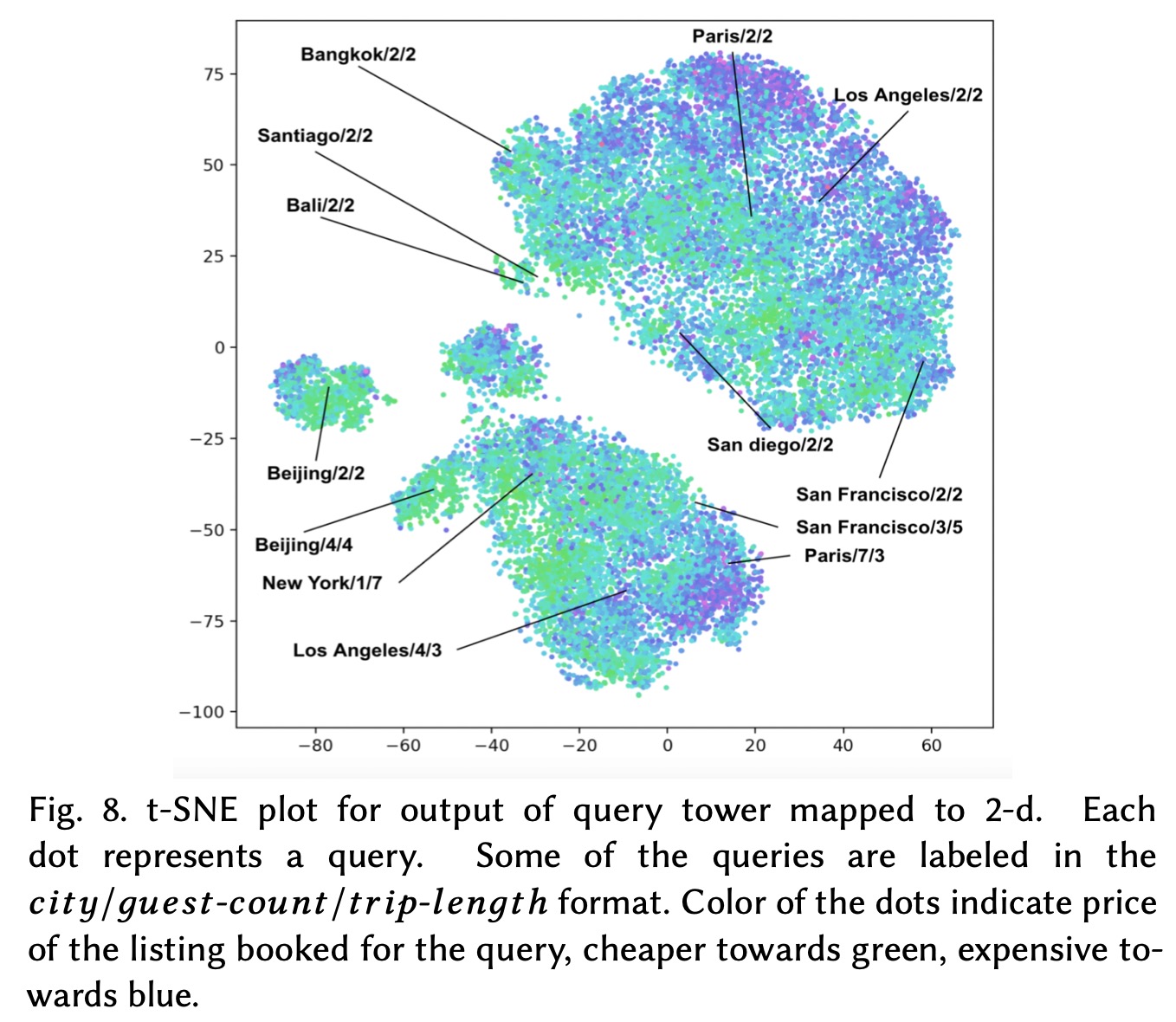
我们可以发现旅行人数和旅行时间长短相近的向量,在位置上也更为集中,同时直觉上相近的城市也处于相近的位置。同时也可以发现,这些聚类并不是价格聚类,我们用不同颜色表示价格,我们可以发现不同聚类都包含不同的颜色点。
Improving Cold Start
在我们的场景中,很大比例的用户对于我们都是新用户,处理用户级别的冷启动就是ranking的一部分,所以我们这里说的冷启动问题,更多的是物品的冷启动。
使用NDCG来衡量预定房间在搜索结果中位置的好坏是一个比较可靠的方式,所以最直观的方式就是去找那些远低于平均NDCG的case,然后我们发现新的房间相比于整体会低6%,这说明我们的模型很难衡量一个用户对于新物品的喜好,为了更好的理解这一点,我们将历史交互信息从特征中移除,我们发现NDCG降低了4.5%,所以我们的模型严重依赖于这些参与的特征,这也就说明了为什么模型在新房间上表现较差。
Approaching Cold Start As E&E
解决冷启动的一个做法就是在E&E上做权衡,具体做法为对于新的listing,提高它的排序位置,但这种模式有一些挑战:
- 对于新的listing提高排序,会需要在降低短期内的用户体验,增加新的listing改善长期的用户体验中做权衡,由于缺乏明确的目标定义,这样做并不是一个合理的解决方案
- 即使是在固定一定预算来做探索,预算的使用也会受到供需的影响
Estimating Future User Engagement
我们退后了一步,问自己:究竟是什么使得新的listing不同,这个问题的答案就在于新的lisitng缺乏参与特征,比如说历史的预约、点击、浏览次数等等,其他特征如价格、位置等等都是确定的。所以理论上来说,如果我么能预测一个listing的参与特征,那么就能解决冷启动问题。
所以我们尝试把这个冷启动问题作为一个参与特征值的估计问题,这使得我们可以有一个明确的目标,来不断迭代模型优化改进这个问题。为了解决冷启动,我们介绍一个预测的模块,在训练和线上打分时都会用到,为了衡量这个模块的好坏,我们进行以下几步:
- 从log中采样出数亿样本,对于每次搜索结果,随机选出top100的listing,这些listing都是被用户充分“互动”过的
- 令\(R_\text{real}\)表示采样出来的listing的真实排序,discounted rank表示为\(DR_\text{real}=\log(2)/\log(2+R_\text{real})\)
- 对于采样出来的样本,移除参与特征,并用预测值代替,然后重新打分,计算出新的排序\(DR_\text{predicted}\)
- 对于采样的listing,计算误差\((DR_\text{real}-DR_{predicted})^2\)
- 计算采样listing的误差的平均
我们对比了两种方式,baseline为采用默认值填充,另一种方式是采用区域的近邻listing的平均,为了提高准确率,只考虑了容量相同的listing,取季节时间滑窗的平均,一种类似Bayes推荐的做法。
Test Results
在离线分析中,参与特征的预测相比baseline,误差降低42%,线上AB实验中,新的listing的预定增加了14%,全局上增加了0.38%。
Elimaating Positional Bias
在我们查看NDCG偏低的样本时,我们发现精品酒店、传统的床以及早餐,这类listing在我们的候选中却是高速增长的,我们对此的假设是在之前的训练数据中,这些样本受到了位置偏差的影响,并没有排序在最优的位置。
Related Work
给定用户\(u\)和查询\(q\),用户预订一个listing \(l\)的搜索结果可以分成两部分因素:
- listing和用户的相关性,\(P(\text{relevant}=1|l,u,q)\)
- 用户查看位置\(k\)的结果的概率,\(P(\text{examined}=1|k,u,q)\)
后者仅依赖于排序,与展示的listing无关,所以预定的概率应该为 \[ P_\text{booking}=P(\text{relevant}=1|l,u,q) \cdot P(\text{examined}=1|k,u,q) \] 理想情况应该是我们只关注于前者,只根据相关性进行排序,为了达成这个,我们需要
- 一个propensity model来预测\(P(\text{examined}=1|k,u,q)\)
- 用预测的逆概率对训练样本加权
Position As Control Variable
我们的解决方案有两个点,首先它并不干扰线上策略,并不需要对搜索结果做随机,我们依靠一些airbnb特有的性质来将listing展示在搜索结果不同位置:
- listing是在一定周期内可预定的,但不可预约时候,这个listing的位置会降低
- 每个listing都有独一无二的可预定日期,所以不同的listing会因日期变化,展示在不同的位置上
第二点就是我们并不显示的建模propensity model,我们引入一个位置特征,同时用dropout做正则化,在预测时,我们将position feature置为0。
我们将DNN的结果表示为 \[ \text{dnn}_\theta(q,u,l)=\text{rel}_\theta(q,u,l)\cdot\text{pbias}_\theta(q,u,l) \] 这里的\(\text{rel}_\theta(q,u,l)\)估计\(P(\text{relevant}=1|l,u,q)\),\(\text{pbias}_\theta(q,u,l)\)估计\(P(\text{examined}=1|k,u,q)\),我们称之为位置偏差预测。\(\text{pbias}_\theta(q,u,l)\)中缺少listing的位置\(k\)作为输入,因为这个概率会依赖于位置\(k\)。所以我们第一步就是把位置作为特征加入DNN,所以整体变为 \[ \text{dnn}_\theta(q,u,l,k)=\text{rel}_\theta(q,u,l,k)\cdot\text{pbias}_\theta(q,u,l,k) \] 又因为\(P(\text{examined}=1|k,u,q)\)独立与\(l\),任何与\(l\)有关的相关性都可以认为是误差,假设我们有充足的训练数据,我们的DNN输出变成 \[ \text{dnn}_\theta(q,u,l,k)=\text{rel}_\theta(q,u,l,k)\cdot\text{pbias}_\theta(q,u,k) \] 当做推断的时候,我们将位置特征\(k\)设置为0,我们用\(Q\)和\(U\)表示查询和用户特征,所以给定查询,后面的位置偏差预测变成一个固定的常数 \[ \text{dnn}_\theta(Q,U,l,0)=\text{rel}_\theta(Q,U,l,0)\cdot\beta \] 这就使得我们的结果独立与位置偏差,只依赖于listing的相关性。
Position Dropout
加入这样position的模型假设后,可以有效降低位置选择偏差的问题,但也引来了新的问题,相关性的预测依赖于位置特征,这就使得DNN在训练中依赖位置特征,在线上预测时候缺失这个特征,与baseline相比,模型NDCG低1.3%。为了相关性预测的依赖,我们引入dropout作为正则,在训练中我们将这维特征设为0,并通过dropout rate控制。我们尝试通过比较不同dropout rate下的NDCG来选择合适的取值。
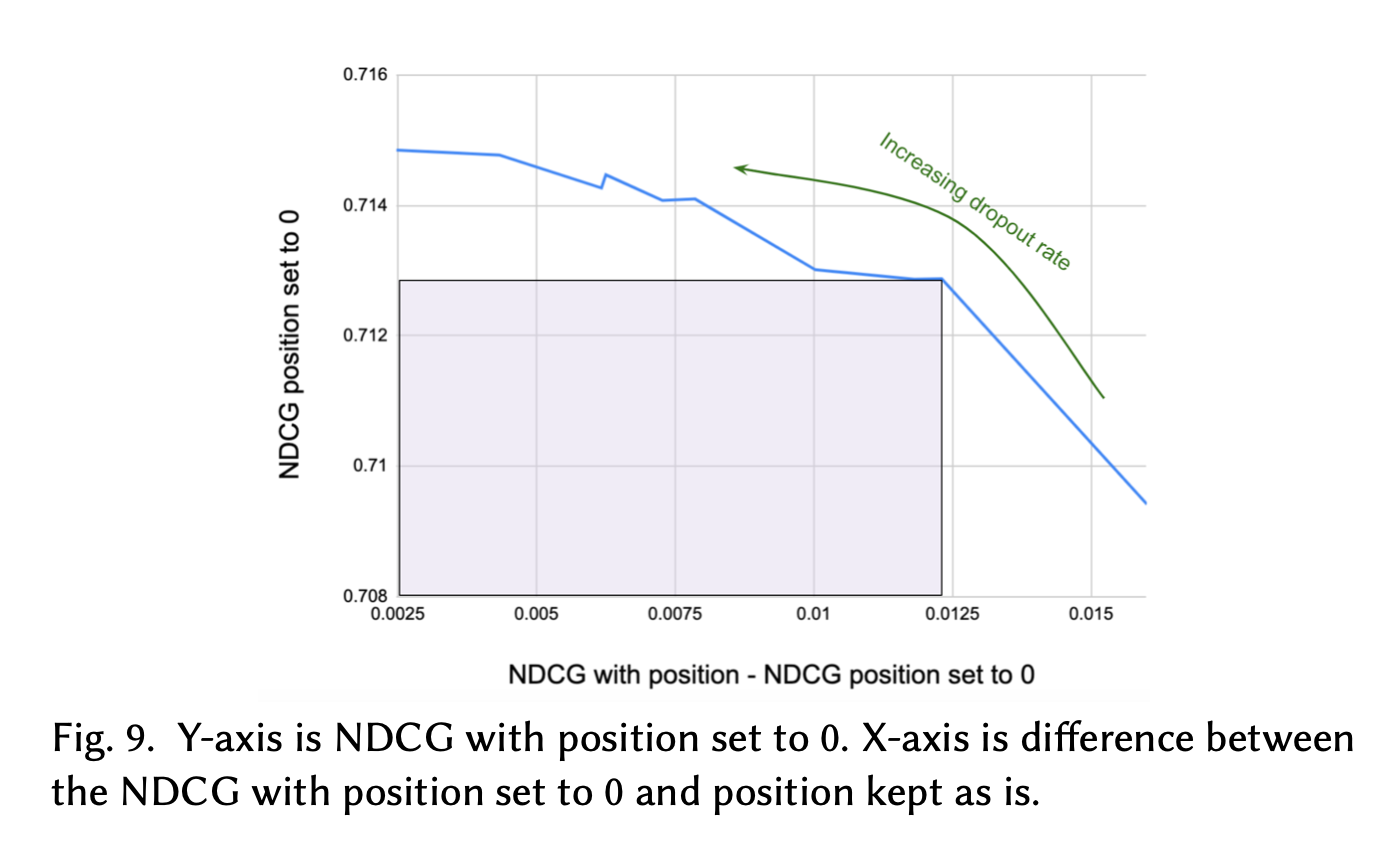
Test Results
线上AB测试,预定增加0.7%,同时收益增加1.8%,