正文

先读Abstract。

Accurate predictions of customers’ future lifetime value (LTV) given their attributes and past purchase behavior enables a more customer-centric marketing strategy. Marketers can segment customers into various buckets based on the predicted LTV and, in turn, customize marketing messages or advertising copies to serve customers in different segments better. Furthermore, LTV predictions can directly inform marketing budget allocations and improve real-time targeting and bidding of ad impressions.

One challenge of LTV modeling is that some customers never come back, and the distribution of LTV can be heavy-tailed. The commonly used mean squared error (MSE) loss does not accommodate the significant fraction of zero value LTV from one-time purchasers and can be sensitive to extremely large LTV’s from top spenders. In this article, we model the distribution of LTV given associated features as a mixture of zero point mass and lognormal distribution, which we refer to as the zero-inflated lognormal (ZILN) distribution. This modeling approach allows us to capture the churn probability and account for the heavy-tailedness nature of LTV at the same time. It also yields straightforward uncertainty quantification of the point prediction. The ZILN loss can be used in both linear models and deep neural networks (DNN). For model evaluation, we recommend the normalized Gini coefficient to quantify model discrimination and decile charts to assess model cali- bration. Empirically, we demonstrate the predictive performance of our proposed model on two real-world public datasets.

基于用户的属性和过去的购买行为，准确预测客户未来生命周期价值（LTV），可以实现更以客户为中心的营销策略。营销人员可以根据预测的LTV将客户划分为不同的类别，进而定制营销信息或广告方案，以更好地服务不同类别的客户。除此之外，LTV也可以直接影响营销预算分配以及广告竞价。

LTV建模的一个挑战是一些用户在来访之后就不会回访了，同时其它用户的LTV分布是长尾的形状。通用的MSE损失并不能适应这些单次购买后就流失的零值用户，同时对于特别头部的高购用户也会变得十分敏感。

在这篇文章中，我们将LTV的分布建模成一种包含0点和log normal的混合分布，称之为zero-inflated lognormal (ZILN) 分布。这种建模方式允许我们既可以建模到用户流失的概率，也能够考虑到后续长尾的LTV分布，同时也能直接产出点预测的不确定性。

ZILN损失既可以用于线性模型也可以用于深度神经网络。在模型评估上，我们推荐采用标准化的Gini系数来度量模型的区分度，以及用分位数图表来评估模型的校准程度。我们在两个真实的开放数据集上评估了我们模型的表现。

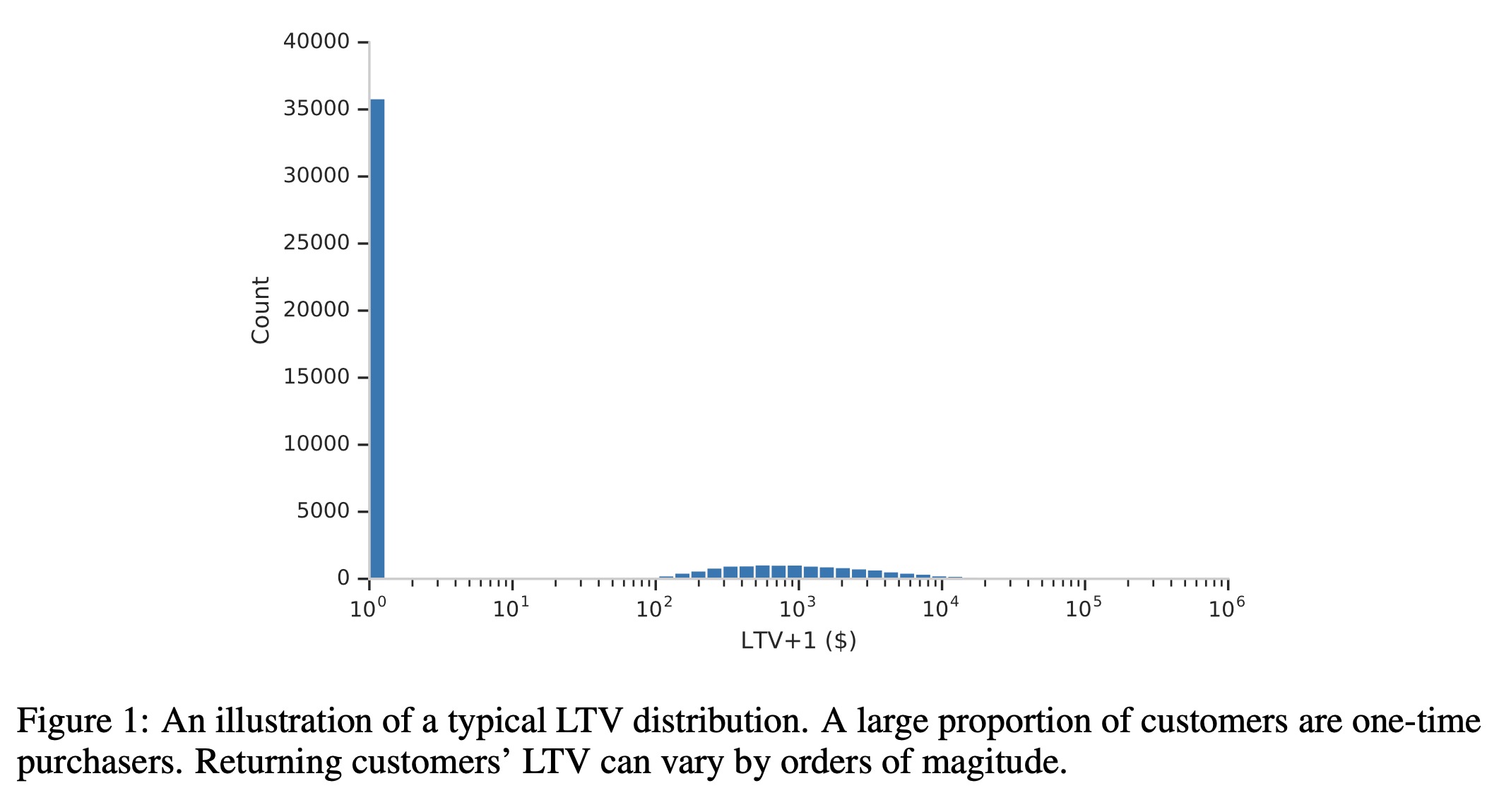
上图是一个真实LTV分布的图示，会存在大量的0值，除此之外其他值会成一个长尾的分布，如果采用MSE作为损失函数，会过度惩罚那些高值的样本。用分位数损失函数替代虽然可以避免这个问题，但是模型无法预测LTV的期望，后续使用时候会存在困难。

本文提出一种基于ZILN分布的负对数似然函数的混合损失函数，这种混合损失能同时学习购买概率和商业价值。其中对数正态部分表示为 \[ \ell_\text{LogNormal}(x;\mu,\sigma)=\log (x\sigma\sqrt{2\pi})+\frac{(\log x-\mu)^2}{2\sigma^2} \] 其中均值函数\(\mu\)和标准差函数\(\sigma\)。这部分可以看作是对于log变化后的X关于MSE损失的加权，其中\(\sigma\)作为权重参数。除此之外，标准差函数也可以依赖于输入的特征，就像均值参数一样，可以得到一个不同形状的LTV分布。 \[ \mathbb{E}[X] = \exp\Big( \mu +\frac{\sigma^2}{2} \Big) \] 下图对比了MSE和对数正态损失，MSE会对称地惩罚两边的偏离值，对数正态损失会更少惩罚较高的取值，最小值也会随着\(\sigma\)增加而增加。

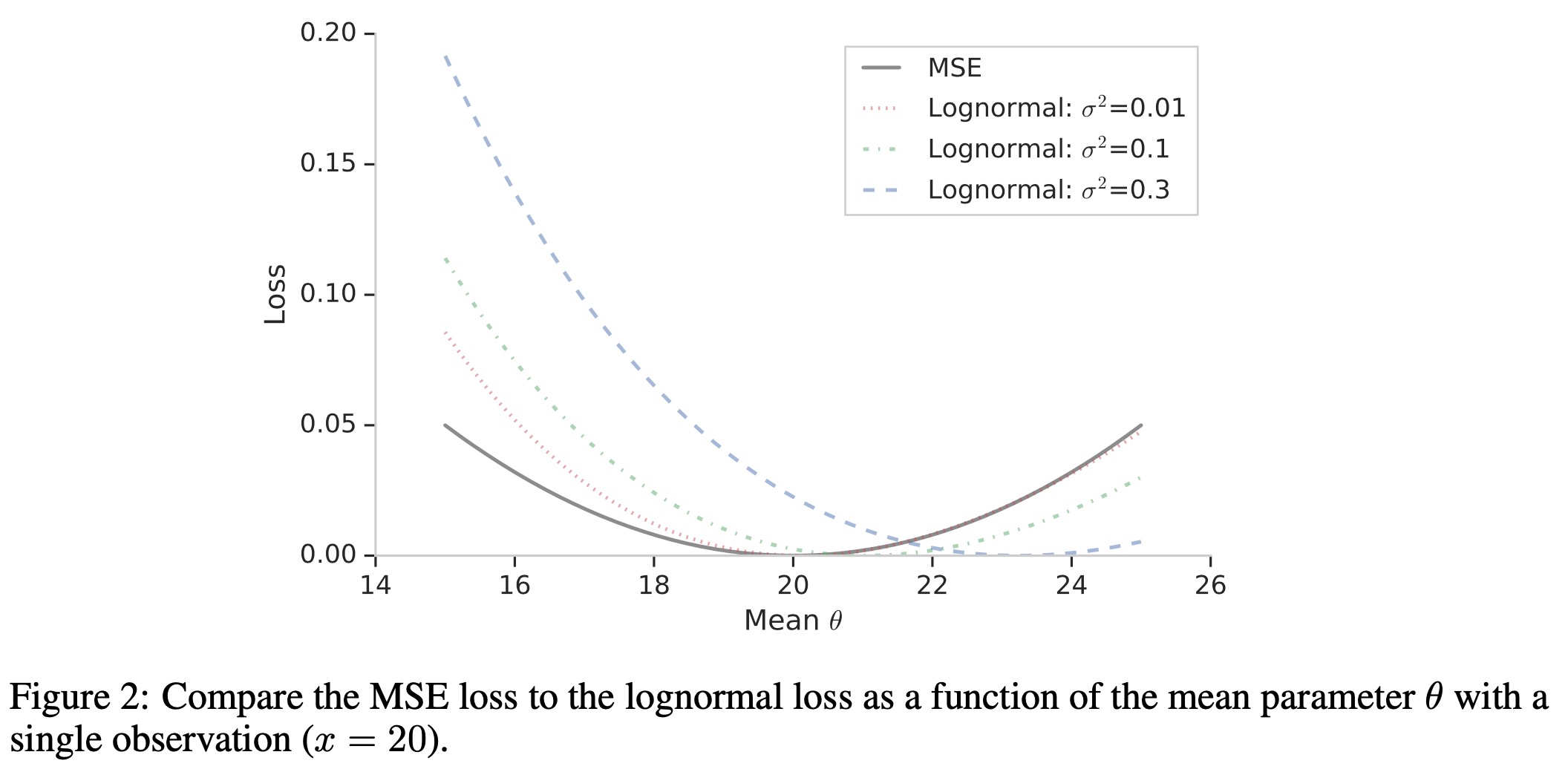
ZILN loss完整如下 \[ \ell_\text{ZLIN}(x;p,\mu,\sigma)=\ell_\text{CrossEntropy}(\mathbb{I}_{x>0};p)+\mathbb{I}_{x>0}\ell_\text{LogNormal}(x;\mu,\sigma) \] 网络结构如下图所示，模型有三个输出，分别输出购买概率\(p\)、均值\(\mu\)和方差\(\sigma\)。

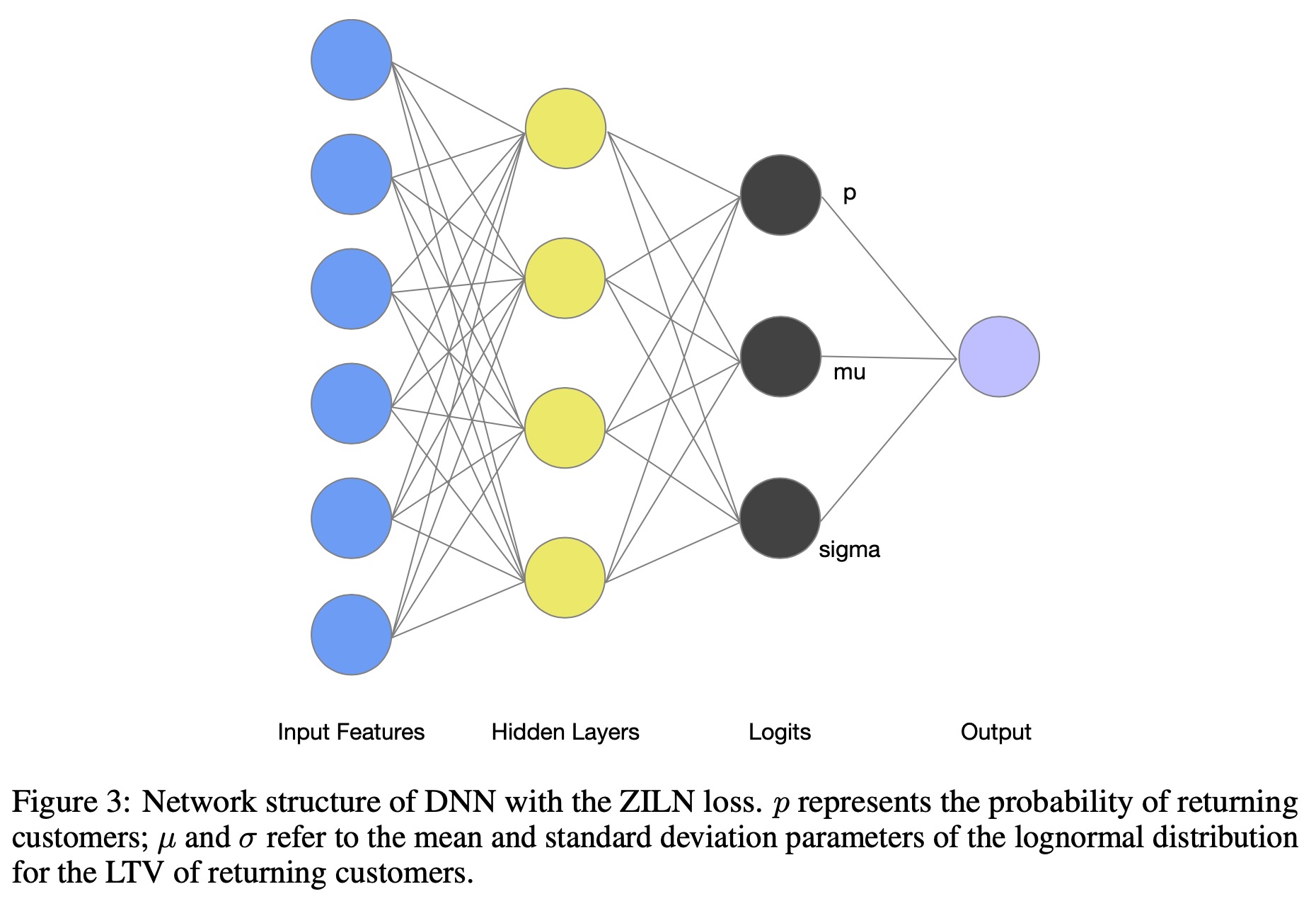
ZILN损失另一个优势是它提供了完整的分布预测，不仅可以得到客户流失的概率，同时也能对留存用户的商业价值进行预测。

本文还有一个很有价值的点在于提出了一些评估LTV的方法。文中认为除了传统的评估方式外，还需要考虑模型的区分度和校准值，区分度表明模型具备将高价值客户区分出来的能力，校准值指模型的预测值和真实值应该一致。

对于区分度的评估，文中提出用Gini系数来评估，将所有样本按预测值排序，用该样本的真实值做纵轴，计算累积top k%的用户LTV值

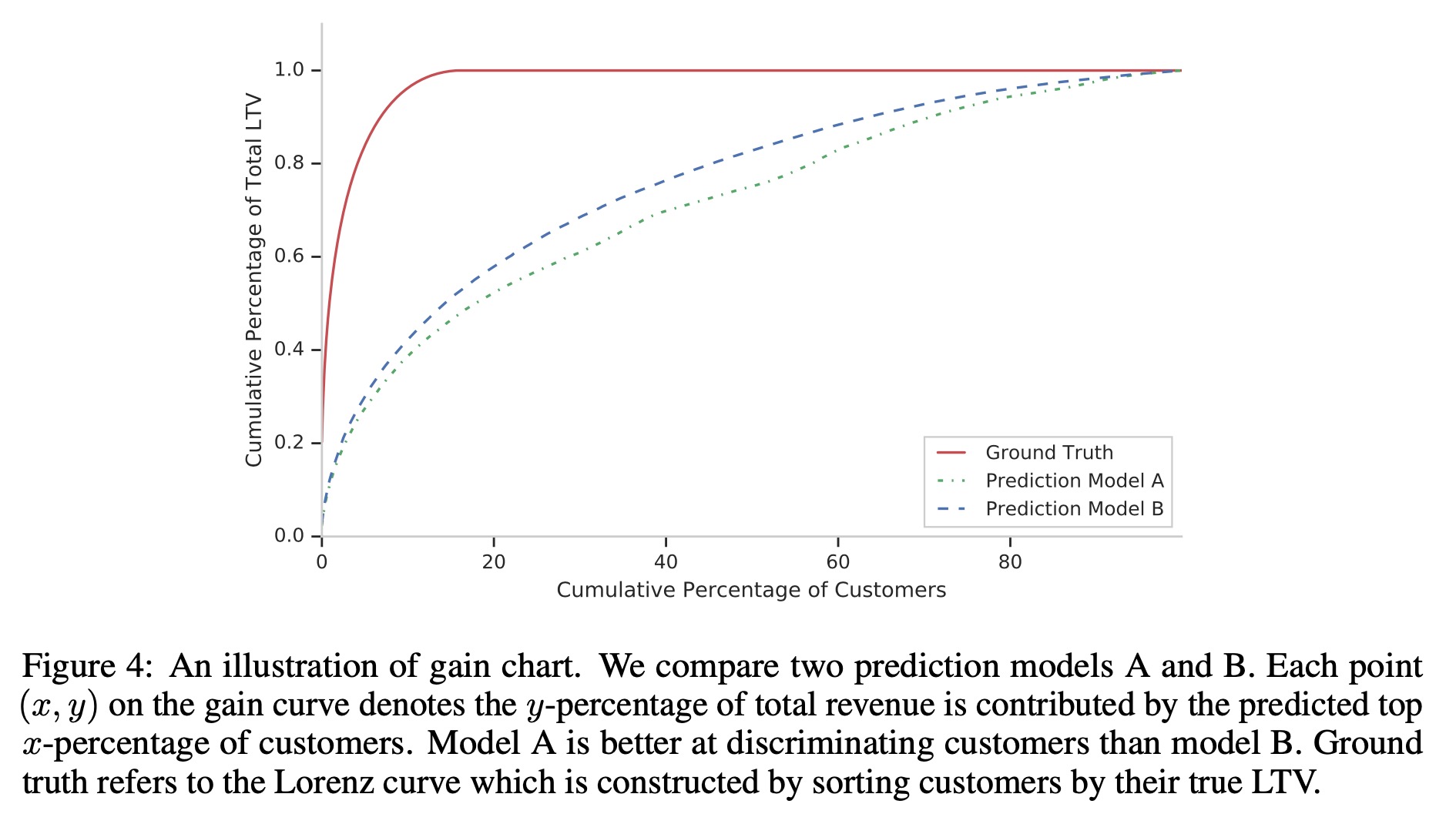
对于校准程度，采用分位数分桶的方式，来比较不同分桶下的预测值和实际值的差异

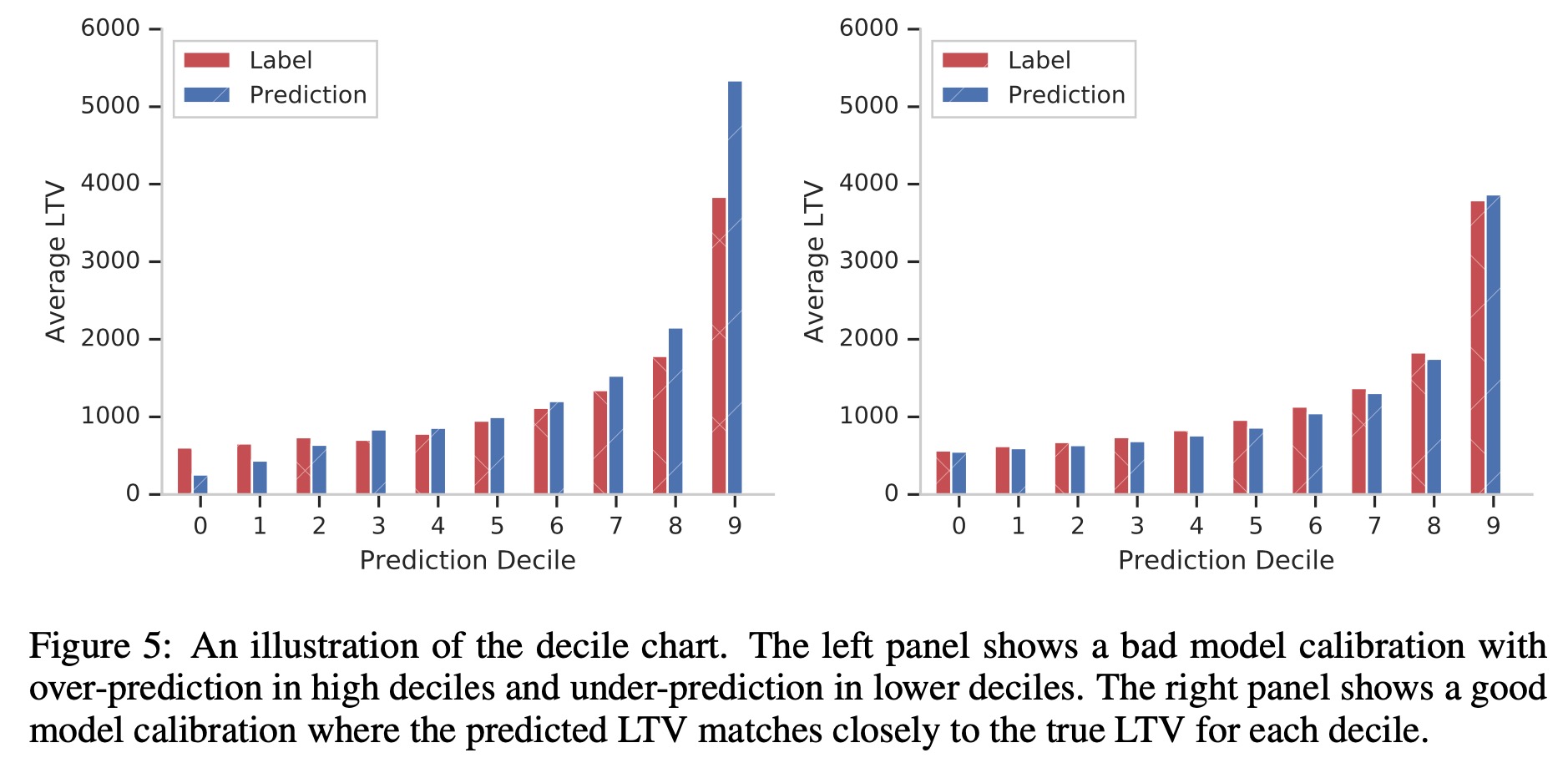
文中后续比较了两个实际数据集上模型的效果

总结

文章思路比较“朴素”，到现在文章还只是挂在arxiv上。

但是对于LTV而言，怎么预测永远都不是最大的问题，难在如何使用，以及根据使用的方式来评估你模型的好坏，比如说一个LTV预测不准，但是其区分度非常好，依然可以帮助我们圈选出高LTV的用户进行定向的投资。

还有一个我个人比较感兴趣的点，对于特殊分布的回归问题该怎么做。本文中的解决方案是做成混合分布的形式，并通过负似然函数进行优化，这是一种解决方案。联想到之前一些工作，用多分类的方式来近似一个单峰和双峰的混合分布，感觉还是有些东西在的，后面可能会写一下相关的工作。