最近要做一些和广告出价相关的工作，恶补了一下广告相关的知识，这篇文章是WWW2020 腾讯的文章，解决广告场景下的概率校准问题。

问题背景

如果一个模型的概率预测值等于真实的输出，那么就可以说这个机器学习模型是校准良好的（well-calibrated）。当模型在一个测试数据集或者其任意子集上，如果估计概率值为\(p\)，那么实际结果中\(y=1\)的样本占比也应该为\(p\)。

在很多场景上，我们都会依赖于模型的概率预估值做后续的决策，比如在广告或者红包发放的场景下，我们需要用预估的换端率或核销率，来计算期望成本，进而保证预算的约束。但是目前很多机器学习模型，尤其是深度模型，对于概率的校准程度其实是很差的（树模型相对较好），这就导致我们在使用这些模型时，需要对模型的概率预测值做校准。

“无法度量就无法优化”，如果想优化模型预测的校准程度，首先需要先定义如何度量一个模型的校准程度，这是做模型校准的第一个问题。其次我们在优化模型校准程度的时候，是否能够在不破坏模型原有排序能力（比如AUC指标）的基础上，提升预估值准确度。这两个问题是做模型校准时需要考虑的核心问题。

相关工作

此处先简单列举一下前人的工作。

在校准指标上，之前主要集中在logloss、BrierScore和概率误差（Probability-level Calibration Error，Prob-ECE）上。

\[ \begin{aligned} \text{LogLoss} &= -\frac{1}{|\mathcal{D}|}\sum_{i\in\mathcal{D}} \Big[ y_i\log(\hat{p}_i) + (1-y_i)\log(1 -\hat{p}_i) \Big] \\ \text{BrierScore} &= \frac{1}{|\mathcal{D}|}\sum_{i\in\mathcal{D}} (y_i-\hat{p}_i)^2 \\ \text{Prob-ECE} &= \frac{1}{|\mathcal{D}|} \sum_{k\in\mathcal{K}} \Big| \sum_{i\in\mathcal{D}} (y_i - \hat{p}_i) \cdot \mathbb{I}\big(\hat{p}_i\in[a_k,b_k)\big) \Big| \\ \end{aligned} \]

其中LogLoss和BrierScore都是数据集维度的指标，并没有办法度量模型在某个子集上的效果，同时很难直观解释偏差程度。Prob-ECE具体的做法是将概率预测值分\(\mathcal{K}\)桶，然后计算每个桶中的偏差，再求和，这个指标在类别分布极度不均衡时候很难度量好坏，同时如果当模型对所有样本都预测为总体均值时，该误差为0，但此时模型并不具备排序能力。

在SIR算法(OMG竟然是老板的文章)中也提出了一些指标如PCOC（其实是facebook一篇文章中提到的）、Cal-N和GC-N，简单来说就是整体的预测值和真实值的比、分N桶后预测值与真实值、分域分N桶后预测值与真实值的比 \[ \begin{aligned} \text{PCOC} &= \frac{\sum \hat{p}}{\sum y / N}\\ \text{Cal-N} &= \sqrt{\frac{\sum_i \text{error}_i^2}{N}} && \text{error}_i=\begin{cases} \text{PCOC}_i -1 & \text{PCOC}_i \geq 1 \\ 1 / \text{PCOC}_i - 1 & \text{PCOC}_i < 1 \end{cases} \\ \text{GC-N} &= \frac{\sum_j w_j \text{Cal-N}_j}{\sum_j w_j} \end{aligned} \] 在校准方法上，主要分成两大类，第一类是在模型中引入假设或者加入归纳偏置（俗称，loss上一部分）来直接端到端学习一个校准的值，另一类是一种两阶段的方式，在有预估值之后，后置处理做校准。目前第二种做法在业界比较流行，因为做法更灵活，而且能够更好地保留模型排序能力。

常见的后置处理方式包括Scaling、Histogram Binning和Isotonic Regression。

Scaling，我只在facebook很久之前tree+lr的那篇文章中见过，说如果训练时候做了负样本降采样，那么需要在线上使用时候缩放回去，\(q=\frac{p}{p+(1-p)/w}\)，其中\(w\)为采样率。理论上来说，直接对原分布做均值平移和方差缩放，也可以做到校准的效果。
Histogram Binning，分桶的做法，即将模型的预估值排序分桶后，用桶内样本的真实均值来替代模型的预估值。
Isotonic Regression，保序回归，简单来说就是模型按预测值排序后，按照保序的逻辑来产出一个新的label，然后重新拟合，细可以看sklearn中的保序回归，讲的非常清楚，我这里只贴一张图。

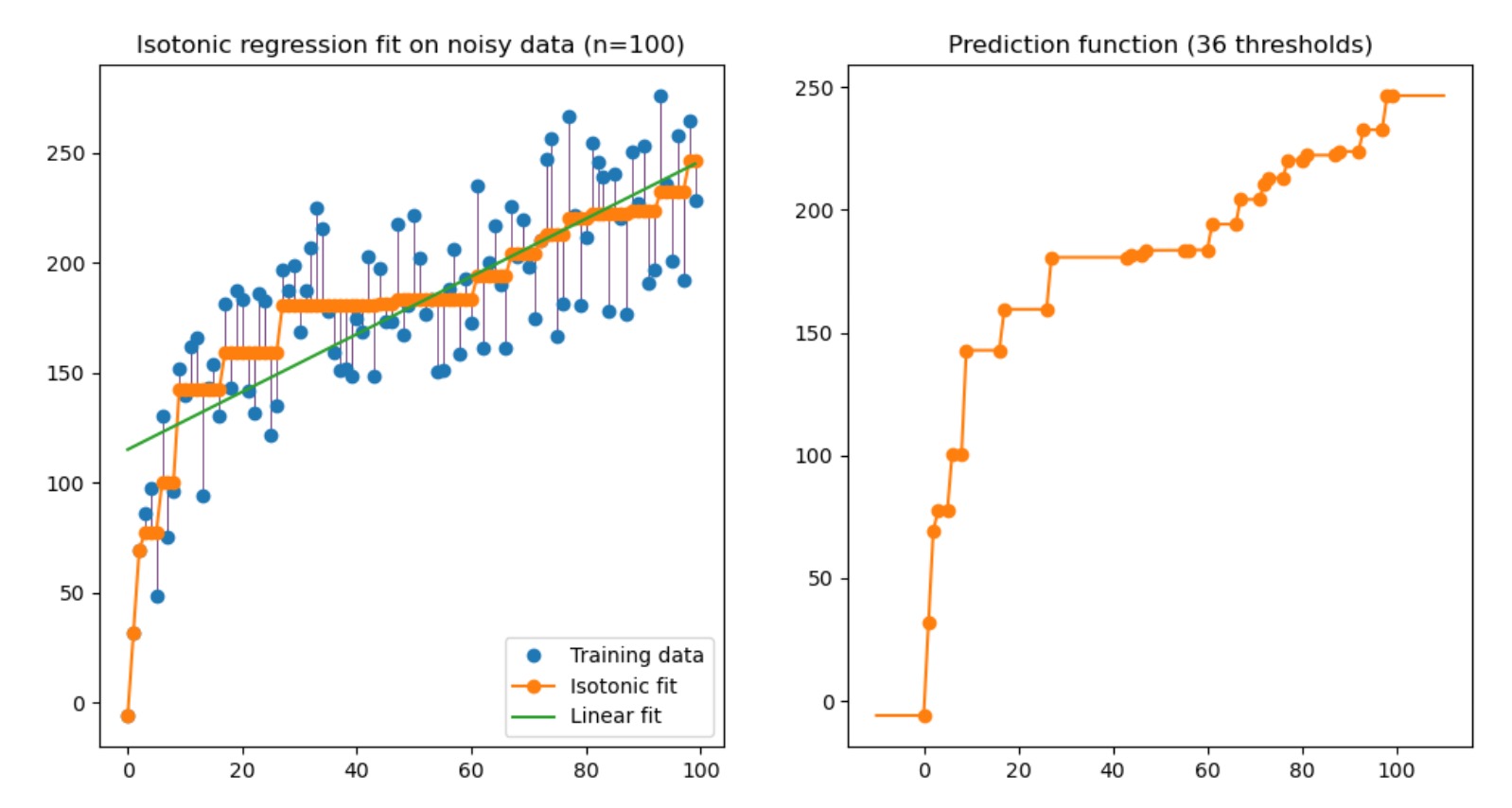
上面这三种方式，Histogram Binning在分桶比较粗的时候（为了trade-off桶内样本置信度）时候，会影响排序指标，scaling和Isotonic Regression不会影响排序指标。

除了这几种基础的之外，还有一个SIR算法（Smoothed Isotonic Regression），具体做法是结合分桶校准和保序回归，做法为先对模型预估值进行排序分桶，然后对于不同桶之间的值进行保序回归，再将桶和桶中值进行线性插值，作为样本的估计值。

SIR的基础上还衍生了Bayes-SIR和RTW-BSIR，分别用于解决冷启动和时序波动的问题，此处不过多展开。

解决方案

新指标叫Field-level Calibration Error，计算方式为 \[ \begin{aligned} \text{Field-ECE} &= \frac{1}{|\mathcal{D}|} \sum_{z\in\mathcal{Z}} \Big| \sum_{i\in\mathcal{D}} (y_i - \hat{p}_i)\cdot \mathbb{I}\big(z_i=z\big) \Big| \\ \text{Field-RCE} &= \frac{1}{|\mathcal{D}|} \sum_{z\in\mathcal{Z}} N_z \frac{ \Big|\sum_{i\in\mathcal{D}} (y_i - \hat{p}_i)\cdot \mathbb{I}\big(z_i=z\big) \Big| }{ \sum_{i\in\mathcal{D}} (y_i + \epsilon ) \cdot \mathbb{I}\big(z_i=z\big) } \end{aligned} \] 其中\(\mathcal{Z}\)表示某个域下划分，比如按年龄段划分有10个值，那\(\mathcal{Z}=\{1,\cdots,10\}\)，将测试集可以分成10个子集，Field-ECE是将每个子集内计算绝对误差再求和，Field-RCE是在原来Field-ECE基础上考虑某个域下的真实正例比例，避免因为绝对值得问题造成偏差。有点类似APE、MAPE和WMAPE的思路。

模型方面，文中提出一种基于NN的校准模型，如下图所示

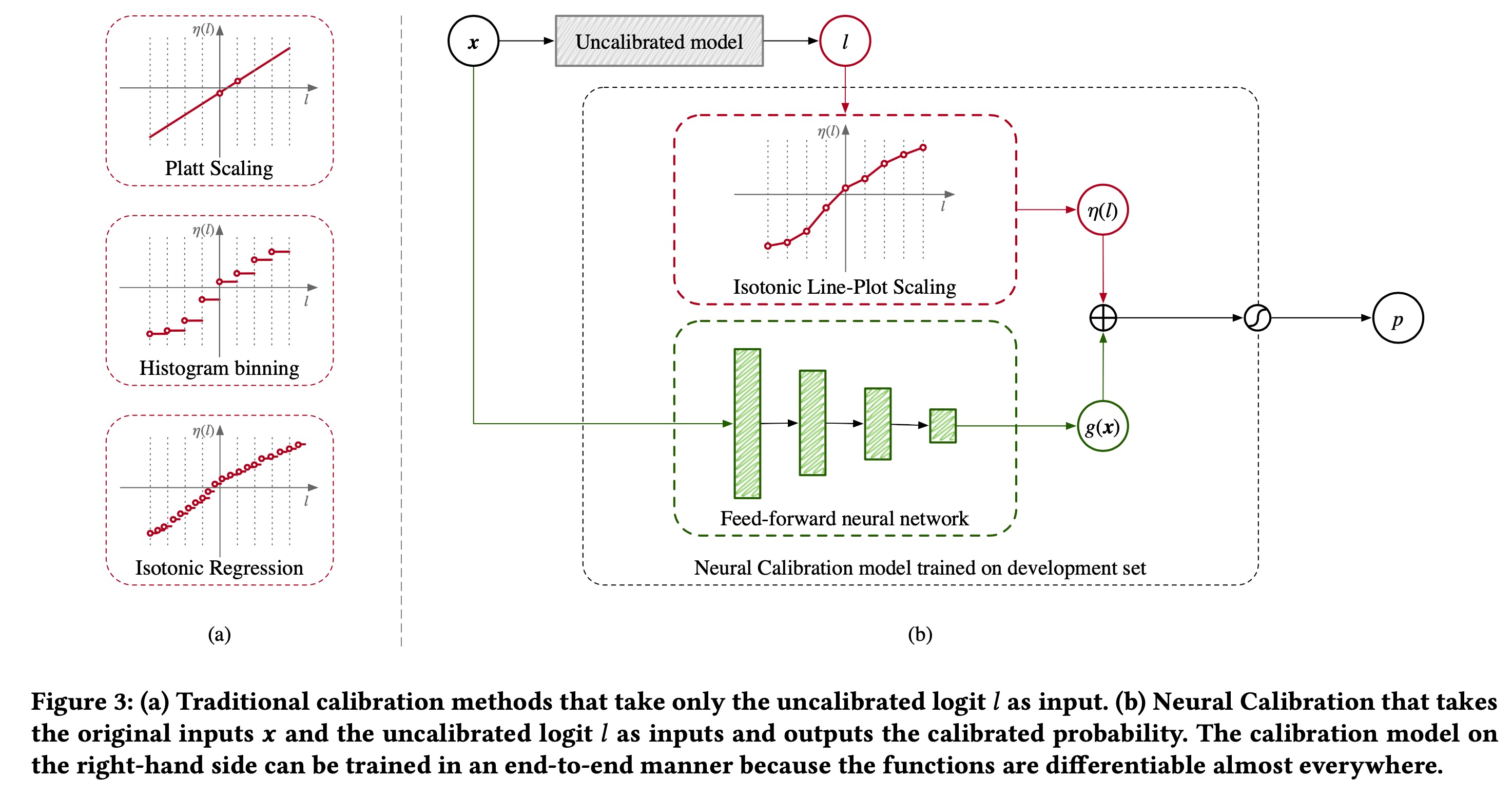
校准后的输出由两部分组成 \[ q(l,x)=\sigma(\eta(l) + g(x)) \] 第一部分是一个对于原始输出logit的分布校准，具体做法是做分桶后，自动学习一个新的logit值，新的logit值可以理解为是在一个桶内的线性插值。 \[ \begin{aligned} \eta(l) &= b + \sum_{k\in\mathcal{K}} w_k \min\{ (l-a_k)_+, a_{k+1} - a_k\} \\ \eta(l) &\approx \sum_{k\in\mathcal{K}}\Big[b_k +(l-a_k)\frac{b_{k+1} - b_k}{a_{k+1} - a_k} \Big] \cdot \mathbb{I}\Big(l\in[a_k, a_{k+1})\Big) \end{aligned} \] 此处有一个近似的做法，将未校准的logit \(l\)做分桶，每个桶阈值为\([a_k, a_{k+1})\)，然后我们希望学习的参数为\(b_k\)，在TF中可以直接用feature_column实现，做boundry的分桶后，输出one_hot和1维embedding，1维embedding就是\(b_k\)，one_hot是后面的指示函数，\(l-a_k\)可以做做预处理，当成raw_feature传入。

在Loss层面，希望\(b_k\)是保序的，所以加入正则项 \[ \mathcal{L}_\text{ILPS}(b;y,l)=\text{LogLoss}(\eta(l),y) +\lambda\sum_{k\in\mathcal{K}}(b_k - b_{k+1})_+ \] 模型第二部分，是作为一个分域的bias校准，由\(g(x)\)来学习某个域上的bias，这个就是一个简单的NN网络。

整体模型训练分4步：

训练集\(\mathcal{D}_\text{train}\)训练基础模型\(f\)，验证集\(\mathcal{D}_\text{dev}\)做超参数调整
用模型\(f\)预测验证集
用验证集数据学习\(q(l,x)=\sigma(\eta(l)+g(x))\)
线上使用\(q(x)=\sigma(\eta(f(x))+g(x))\)

实验

第一篇文章的实验还是比较丰满的，此处列举一些实验观察

增加训练数据对于AUC有提升，但并不一定能降低校准误差
整体校准误差小并不代表着域校准误差小
传统校准方式可能在校准指标更好，但是AUC会差一些
数据分布偏移下，传统后置校准方式也并不好用
域校准误差相比整体校准误差，更容易观测

一些脑洞

本来想和《MBCT: Tree-Based Feature-Aware Binning for Individual Uncertainty Calibration》这篇文章一起写的，但是看的时候发现里面有一些bound的证明，还没仔细看，就下回再写了。

先记一些我读完这篇文章的脑洞

对于分类问题而言，也是没有个体ground truth的问题，只能从群体角度观察目标优化情况，那GRF（Generalized Random Forest）这种大杀器是不是就很适合这个场景？分裂指标是最大化\(y\)和\(\hat{y}\)的差异，然后在叶子结点内做honest样本校准，同时由于RF的结构，天然可以做online leanring。
文中提到样本量的问题，因为存在校准环节，所以必须要分出一部分样本，那如何更加充分利用样本呢？最近看了一些跟Pathway相关的东西，MMoE做ensemble，用CrossFitting的方式利用全部用本可能是一个解决方法，但是模型的size会大很多。
还有一个老生常谈的问题，校准时遇到数data draft怎么解决？目前我看到的解决方案多数集中在更实时更新模型，比如ODL。我觉得这个问题可能需要分成两类，第一类假设是data背后的truth function改变了，这种目前看只能通过高频次更新模型解决，或者是做一些robust的设计，直接从最终目标来降低损失，第二类是truth function没有变，但是X的分布变了，这个时候就联系到一些causal的方法以及OOD相关的工作。