TL;DR,
本文感觉像是一篇大作业文章,应该还不是终稿,有很多typo而且写得不那么易懂,但Stefan Wager是作者之一。主要讨论两个常见的用于估计“异质处理效应”(HTE)的forest模型,causal forest和model-based forest,这两个模型之间的差异,以及是什么技巧使得这两个模型效果非常好。
结论是,当存在较强confounding时,对于是否施加treatment的indicator做local centering(即orthogonalization)是最重要的,对于随机实验数据,两者之间并没有显著差异,但是面对更为复杂的函数关系,对treatment indicator和outcome都做local centering会有一定效果提升,即使此时并没有必要针对confounding做调整。
我个人经验是,做orthogonalization是HTE估计是有提升的,对于非随机数据而言效果会好很多,honest对于防止过拟合和提升模型泛化准确性非常有效。数据随机但数据少,优先honest再orthogonalization,数据非随机,一定要orthogonalization,数据多且随机,大概率模型调调参做好就行。
问题定义 & 模型
定义模型形式为 \[ Y = \mu({\rm{X}}) + \tau({\rm{X}}) W +\phi Z \] 其中\(Y\in \Bbb{R}\)是outcome,变量\({\Bbb{X}}\in{\cal{X}}\),二元变量\(W\in\{0,1\}\)表示是否施加treatment,对于给定特征值下,是否施加干预服从二项分布,均值为\(\pi({\rm{x}})\),\(W|{\rm{X}}=x \sim B(1, \pi({\rm{x}}))\),最后的残差项\({\Bbb{E}}(Z|{\rm{X}},W)=0\),\(\phi>0\)。其条件均值为 \[ {\Bbb{E}(Y|{\rm{X}}=x)}=\mu(x) +\tau(x)\pi(x) =:m(x) \] 其中\(\mu(x)\)也称为prognostic,处理效应\(\tau(x)\)也称为predictive(应该是医学术语,model-based forest中提到的)。干预的分配机制假设是非确定的,即propensity score是介于0和1之间 \[ 0 < \pi(x)={\sf{P}}(W=1|{\rm{X}}={\rm{x}})={\Bbb{E}}(W|{\rm{X}}={\rm{x}}) < 1 \] 对于causal forest,采用2-step的方式,第一步先预估\(m({\rm{x}})={\Bbb{E}}(Y|\rm{X=x})\)和\(\pi({\rm{x}})={\Bbb{E}}(W|{\rm{X=x}})\),并且做local centering,\(Y-\hat{m}({\rm{x}})\)和\(W-\hat{\pi}({\rm{x}})\),第二步用残差估计\(\tau({\rm{x}})\),损失函数为 \[ \ell_\text{cf}(\tau) = \frac{1}{2}\Big(Y-\hat{m}({\rm{x}})-\tau({\rm{x}})\big(w-\hat{\pi}({\rm{x}})\big)\Big)^2 \] 做分裂点选择时,首先在父节点中通过最小化上述损失函数,估计一个常量的treatment effect,\(\hat{\tau}\),也即求解 \[ s_\text{cf}(\tau)=\frac{\partial \ell_\text{cf}(\tau)}{\partial \tau} = \Big( Y - \hat{m}({\rm{x}}) - \tau\big(w-\hat{\pi}({\rm{x}})\big) \Big) \big(w - \hat{\pi}({\rm{x}})\big) = 0 \] 然后计算cut-point的score \[ s_\text{cf}(\hat{\tau})=\Big( Y - \hat{m}({\rm{x}}) - \hat{\tau}\big(w-\hat{\pi}({\rm{x}})\big) \Big) \big(w - \hat{\pi}({\rm{x}})\big) \] 选择候选分裂点中,score差异最大的进行树的生长。(文中有证明这和grf中的分裂方式结果是一样的)
对于model-based forest,与causal forest最大的差异在于该模型会同事估计\(\mu({\rm{x}})\)和\(\tau({\rm{x}})\),损失函数为 \[ \ell_\text{mob}(\mu,\tau) = \frac{1}{2}\Big(Y - \mu({\rm{x}}) - \tau({\rm{x}})w\Big)^2 \] 在每个节点中,需要被估计的常量\((\hat{\mu},\hat{\tau})^\mathsf{T}\)通过最小化上述损失函数得到,分裂的特征是通过置换检验得到,其原假设是\(\mu\)和\(\tau\)是一个常量并且独立于其他分裂变量\(\rm{X}\),然后选择p值最低的特征,再通过score选择分裂点的值 \[ s_\text{mob}(\hat{\mu},\hat{\tau}) = (Y - \hat{\mu} - \hat{\tau} w)(1, w)^\mathsf{T} \] (因为这篇文章中,我不太关心model-based forest的具体算法,所以就不做具体展开了)
在样本子集上拟合多个tree共同构成forest,之后两个算法都是采用局部最大似然聚合的方式来估计最后的异质处理效应\(\tau({\rm{x}})\) \[ \hat{\tau}({\rm{x}}) = \underset{\tau}{\arg\min} \sum_i^n \alpha_i^\text{cf}({\rm{x}})\ell_{\text{cf},i}(\tau)\\ \big(\hat{\mu}({\rm{x}}), \hat{\tau}({\rm{x}})\big)^{\mathsf{T}} = \underset{\mu, \tau}{\arg\min} \sum_i^n \alpha_i^\text{mob}({\rm{x}})\ell_{\text{mob},i}(\mu,\tau)\\ \] 其中\(\ell_{\text{cf},i}\)和\(\ell_{\text{mob},i}\)是第\(i\)个样本的损失,\(\alpha_i^\text{cf}\)和\(\alpha_i^\text{mob}\)是forest产出的权重,为样本\(i\)在叶子节点的出现频率。
在cuasl forest中,还额外推荐了一种子样本切分的技术honest,即一个样本要么用来生成树结构,要么用来做最后的预测,honest使其能够达到有效的统计推断(honesty is necessary to accomplish valid statistical inference,个人狭义理解就是可以给出置信区间)。
实验 & 结论
具体实验怎么做的,暂且不关心,感兴趣的可以读原文,此处列举结论。
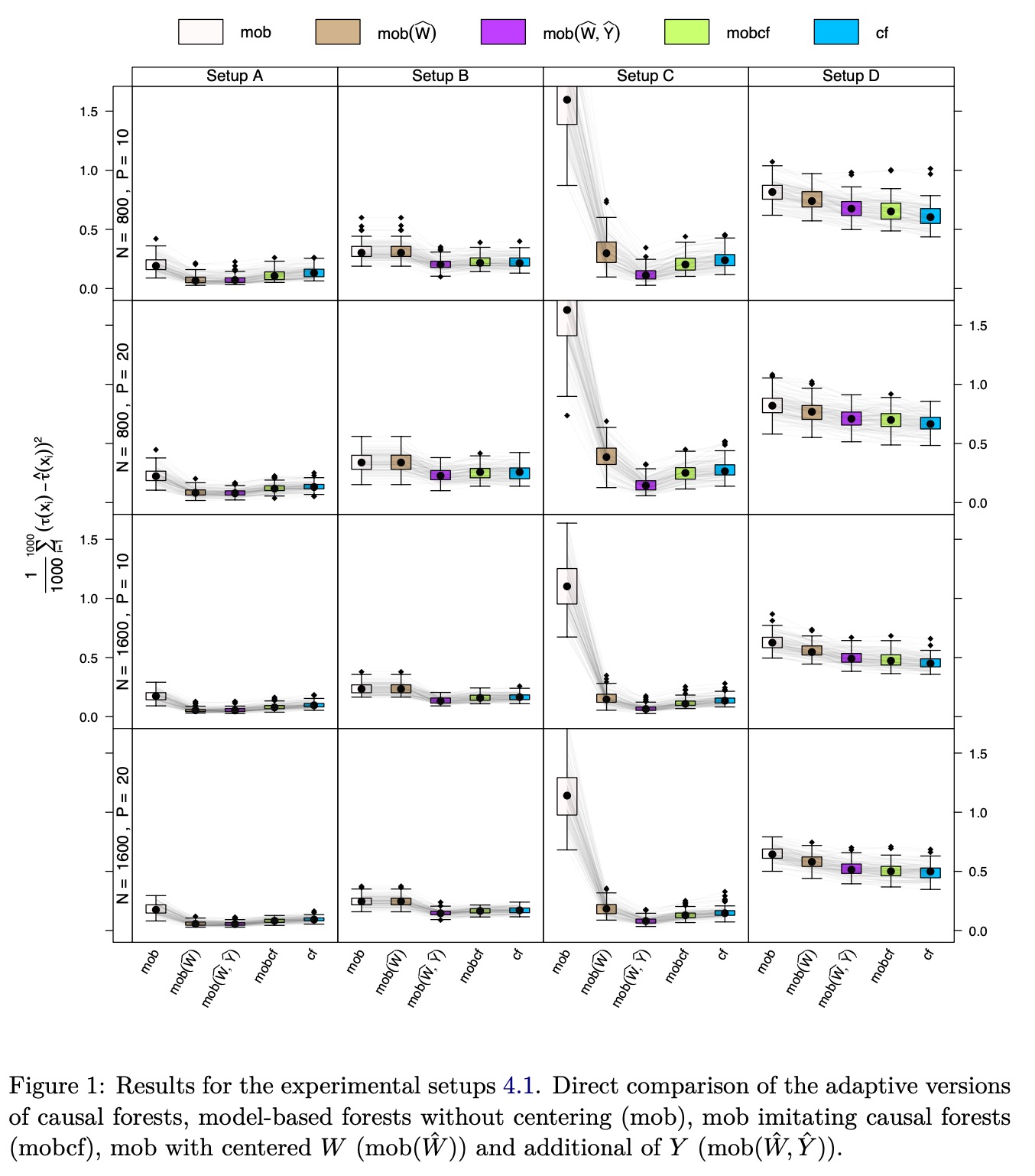
上述对比实验并没有考虑Honest做法。实验结论:
Setup A,比较复杂的confounding,model-based forest很难处理这种情况(该算法常用于随机数据),对\(W\)做local centering是有效的,同时对\(W\)和\(Y\)做并没有进一步提升效果,causal forest有相近的表现,但是会稍微差一点
Setup B,完全随机,同时对\(W\)和\(Y\)做local centering会效果更好,即使此时并没有调整confounding的必要
Setup C,强confounding,没有local centering的模型效果非常差,对于\(W\)做会有很大改进,同时对\(W\)和\(Y\)做提升较小
Setup D,with unrelated treatment and control arms,treatment和control组没有关系,此时所有方法效果都一般(MSE较大),因为这个时候联合建模并没有必要。
综上,对于\(W\)做centering是最有效的手段,如果可以,对\(Y\)也做centering会更好,但是增量可能不大,其他手段对于最终表现影响不大。
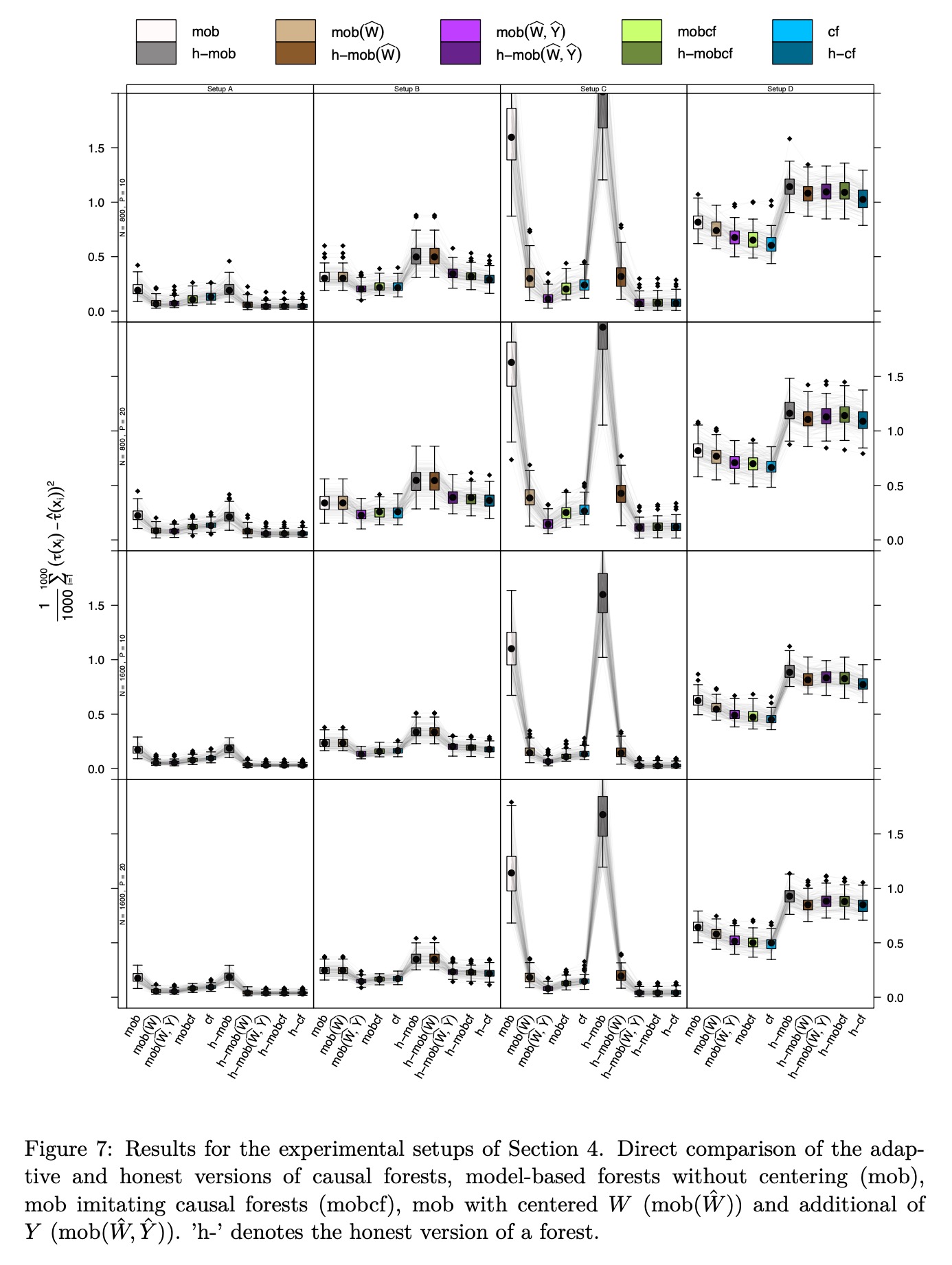
文章的附录中还对比了honest的作用,方法是一样的,结论是honest对于存在confounding的情况会更加有效,随机数据上优势并不大。