Customized Regression Model for Airbnb Dynamic Pricing

发表于 | 分类于

定价相关文章三连。第一篇，kdd2018的airbnb的文章，这篇文章的思路放在当时也是非常巧妙的，在大家都还在用linear regression去fit价格系数时候，这篇文章提出了一种较为新颖的定价模型，在非标品定价的业务场景下具有一定实用价值。这篇文章也是比较早发表在机器学习领域的动态定价相关的文章，当年看完之后对airbnb充满respect。

Introduction

airbnb是一个在线交易网站，将寻求住所的用户和拥有空闲房间的房东相互匹配，在这种双边交易市场中，价格是用来平衡供需的重要抓手。作为平台方，airbnb并不会干涉房东的定价，但是会提供各种各样的工具来帮助房东更高效的设定价格。比如我们允许房东可以个性化的定制每日、每周的价格，或者是一个长期租住的折扣，我们也会为房东提供价格建议，目前有两种方式：

  • Price Tips，我们根据房东设定的价格，给出房间被顶出的概率
  • Smart Pricing，房东只需要提供一个最低最高价格，平台会自动产生推荐价格

由于需求的不确定性，最优价格也会随着变化，这就是一个经典的动态定价问题，aiabnb的房东在一个固定的周期内提供住宿服务。我们的价格建议通过机器学习算法生成，同时每天根据当前市场状态动态给出建议，这个模型的目标是确定一个定价策略，来帮助房东在销售周期内更好地制定价格。

之前的研究中，大部分都是关注于标品定价，通过从历史数据中追踪价格对需求的影响，估计需求曲线\(F(P)\)，然后最大化收益就变成了最大化\(P\times F(P)\)。这种做法的成功关键在于能够精准估计需求函数\(F(P)\)。在airbnb的场景中，需求函数并不仅仅收到价格影响，还受到时间以及房间本身情况的影响，我们将需求函数表示为\(F(P,t,id)\)，其中\(t\)表示时间，\(id\)则是一个房间（airbnb称之为listing）的唯一标识id。

  • 时间的影响，季节周期性变化以及一些特殊节日会影响需求，同时提前预定的时间间隔也会影响需求。
  • 房间本身的影响，跟标准的住宿不同，airbnb上房间都是独一无二的，各有各的特色，不同类型、大小、特色的房价定价是不同的。

这些都会使得我们估计\(F(P,t,id)\)变得困难，除此之外，我们的历史价格可能会有偏，像酒店、航班或者零售商品的定价，公司拥有这些产品的定价权，所以能够做实验或者探索不同的定价策略，来观察市场的反应，但是在airbnb上这些都行不通，平台给出的价格只会被部分房东采用，这使得我们设计定价策略增加了额外的难度。对于使用Price Tips的房东，一般只会在我们的建议价格高于平时的定价时，才会采用。使用Smart Pricing的房东，估计的最优价格可能是超出房东提供的上下限。

本文主要contribution有：

  • 提出了若干个指标，来衡量定价策略的效率
  • 提出一个定制化的回归模型学习定价策略，来降少“差”的价格建议。

PRICING SYSTEM OVERVIEW

定价系统由三个部分组成，首先是一个二分类模型来预测预定概率，然后是一个回归模型来预测最优的价格，第一个模型预估的预定概率会作为第二个模型的输入，最后又一个额外的模块来处理一些特殊的逻辑，诸如特殊节假日等，然后产出最终的价格建议。

定价系统

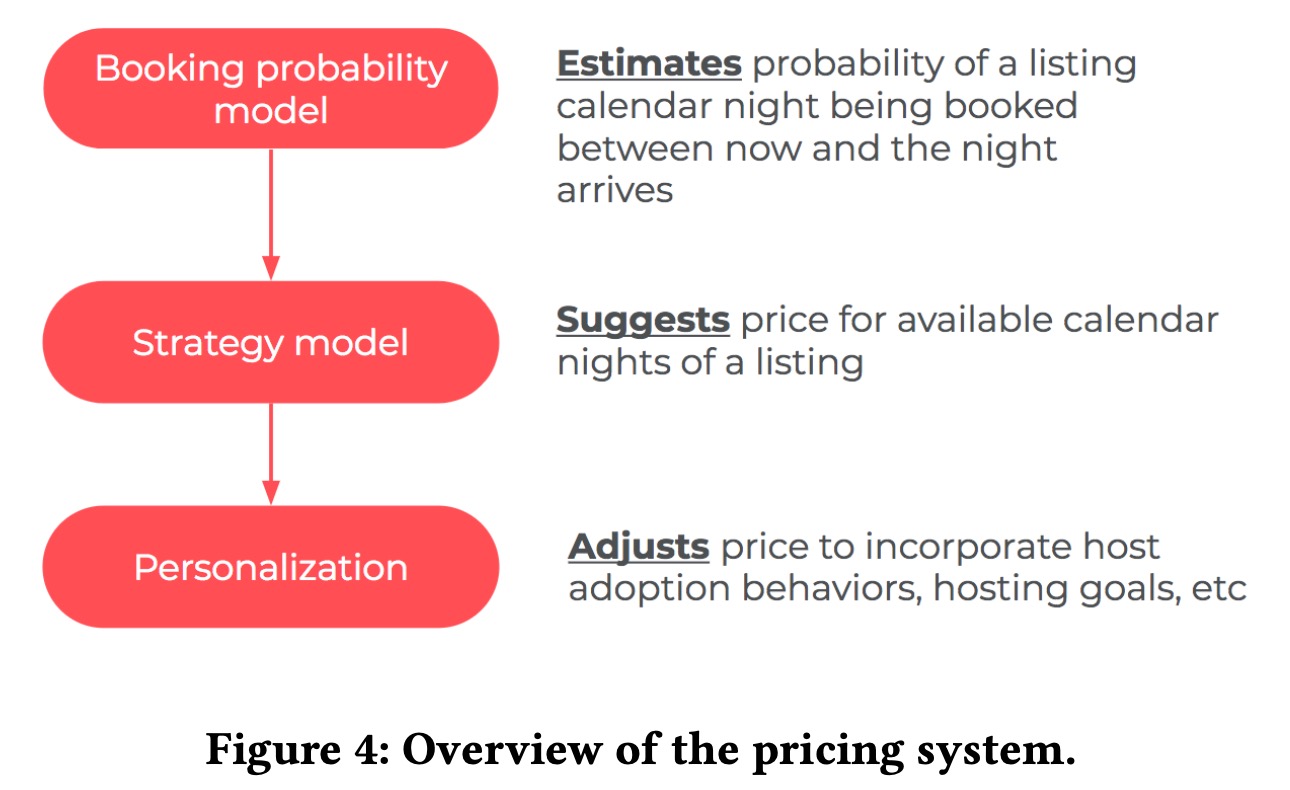
The Booking Probability Model

预定概率预估模型，目标是学习未来的某个夜晚某个房间被预定的概率，采用特征包括：

  • 房间特征，价格、类型、所能入住的人数、各种房价的数量、便利设施、位置、评论、历史预定率、是否能预约等等
  • 时间特征，季节时间、提前预约天数等等
  • 供需特征，附近剩余房间数、浏览量、搜索和联系率等等

我们采用GBM来预估预约概率，我们分市场采用不同的采样比率，以获得更好的表现（auc），对于一个高密度的房间的区域，采用一个更高的采样比率。

概率预估是一个价格的函数，如下图所示

价格曲线

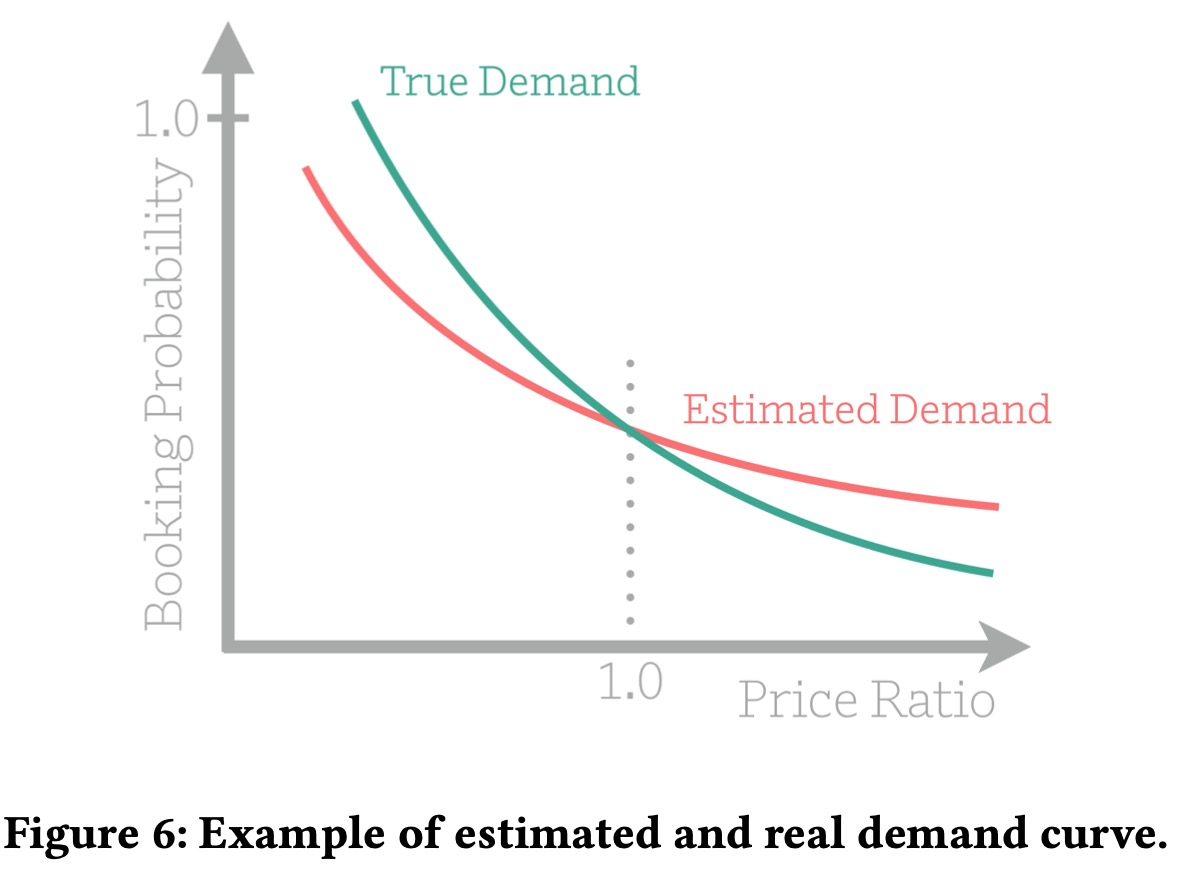
我们希望当价格趋于0时候，预定概率趋于1，价格趋于无穷时，预定概率趋于0。想要精准估计这样的需求曲线主要有三个挑战：

  • 数据稀疏，尤其是同一个房间不同价格
  • 不同房间之间想通的性质比较少，很难泛化学习
  • 特征以来，原始特征是依赖于价格的，比如季节和价格有影响，旺季天然价格会高，淡季价格低，或者是价格高导致预定率低，价格低导致预定率高（数据内生性）

由于这些挑战，我们很难估计出一条需求曲线。我们尝试直接使用收益最大化的策略，但是AB测试的结果表示这样的尝试行不通。因此我们决定采用别的解决方案，以及重新思考什么是最优价格和我们的离线指标应该是什么。

EVALUATING PRICE SUGGESTION

与传统的监督学习问题不同，我们并没有一个“最优”的价格，这使得我们给出的价格无法评估。

我们所提出的指标，是基于我们对于一个“好的”定价的思考，我们\(P\)表示真实的价格，用\(P_{sug}\)表示建议价格，用\(P_o\)表示最优价格，我们认为建议价格是“差的”会满足：

  • 房间被预定，且\(P_{sug}<P\)，价格定低了
  • 房间没有被预定，且\(P_{sug}\geq P\)，价格定高了

也有两种情况我们无法区分价格的好坏：

  • 房间预定了，且\(P_{sug}\geq P\)
  • 房间没被预定，且\(P_{sug}<P\)
样本分类

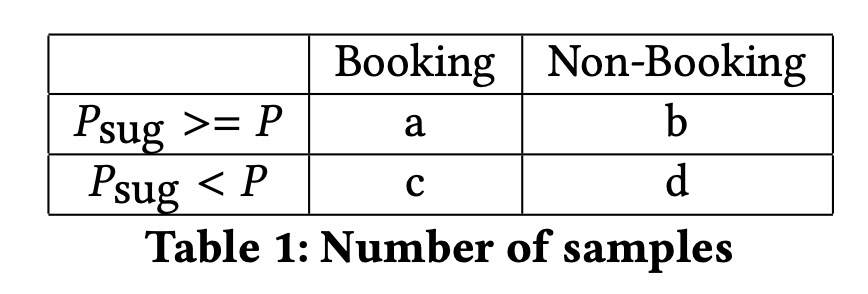
基于以上的观察，我们定义指标：

  • PriceDecreaseRecall(PDR)，\(PDR=\frac{d}{b+d}\)，没有预约的房间中，预估价格低的占比
  • Price Decrease Precision(PDP)，\(PDP=\frac{d}{c+d}\)，建议价格更低的房间中，没有被预约的占比
  • Price Increase Recall(PIR)，\(PIR=\frac{a}{a+c}\)，预约的房间中，预估价格更高的占比
  • Price Increase Precision(PIP)，\(PIP=\frac{a}{a+b}\)，建议价格更高的房间中，被预约的占比
  • Booking Regret(BR)，\(BR=median_{bookings}(\max(0,\frac{P-P_sug}{P}))\)

在以上这些指标中，我们发现PDR和BR与线上的商业指标非常相关，PDR衡量了对于非预定的房间我们建议价格低于当前价格的概率，这种情况，我们的建议价格可能会使得房间更有竞争力。另一方面，BR衡量了我们的建议价格与实际预定价格的偏离程度，这表明了我们的建议价格在市场上是否有竞争力。

STRATEGY MODEL

\(N\)个训练样本\(\{\bf{x}_i,y_i\}_{i=1}^N\)，其中特征\(\bf{x}_i\)包含：

  • 房东设定的价格\(P_i\)
  • 预估的预定概率\(q_i\)
  • 市场需求特征

建议价格表示为\(f_\theta({\bf{x}}_i)\)，其中\(\theta\)是需要学习的参数。下图为我们设计这个loss的思路，我们希望最终预测值落在某个范围内，超出这个范围则会产生loss。

loss

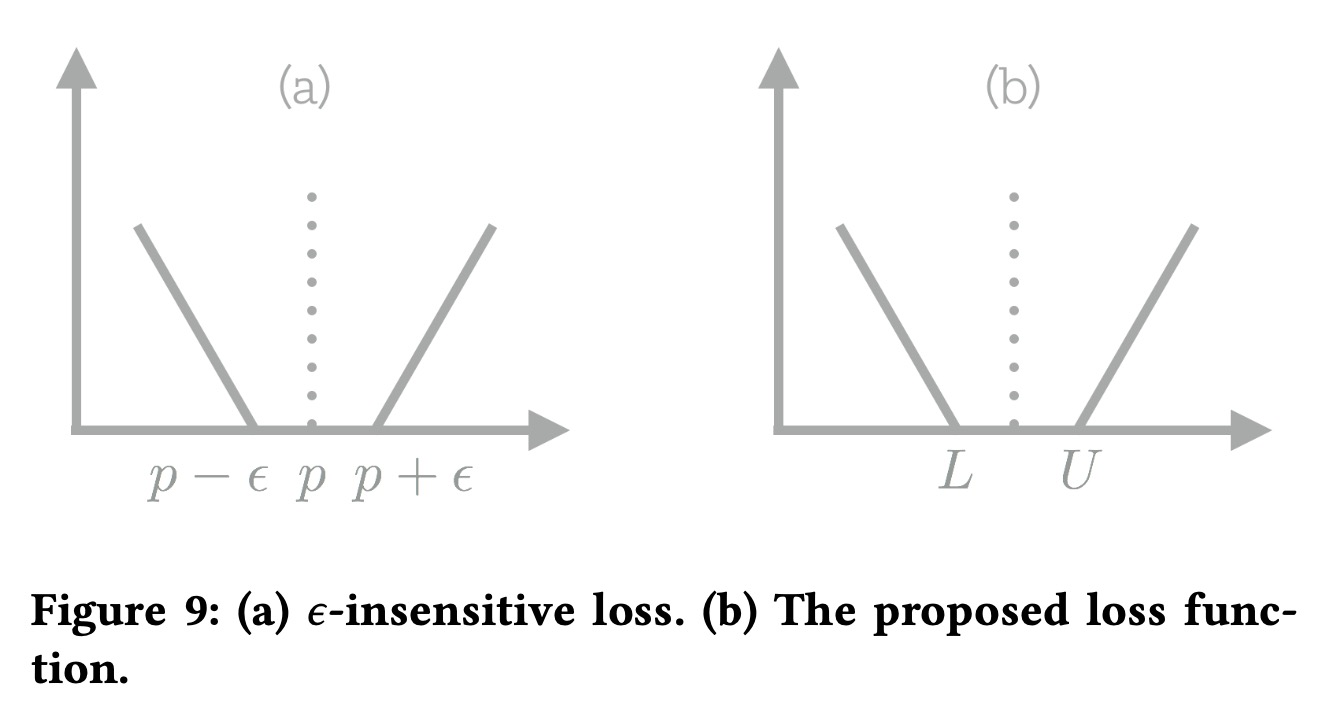
目标函数写为： \[ \mathcal{L}=\underset{\theta}{\arg\min} \sum_{i=1}^N\big( L(P_i, y_i)-f_\theta({\bf{x}}_i) \big)^+ + \big( f_\theta({\bf{x}}_i)-U(P_i, y_i) \big)^+ \] 我们用\(L(P_i,y_i)\)和\(U(P_i,y_i)\)表示上界和下界，如果价格落在中间，则loss为0，如果超过上界或者低于下界，则 \[ L(P_i,y_i)=y_i\cdot P_i + (1-y_i)\cdot c_1 P_i\\ U(P_i,y_i)=(1-y_i)\cdot P_i+y_i\cdot c_2P_i \] 对于被预定的房价，下界是价格\(P_i\)，上界是\(c_2P_i\)，对于未被预定的房价，下界是\(c_1P_i\)，上界是\(P_i\)。

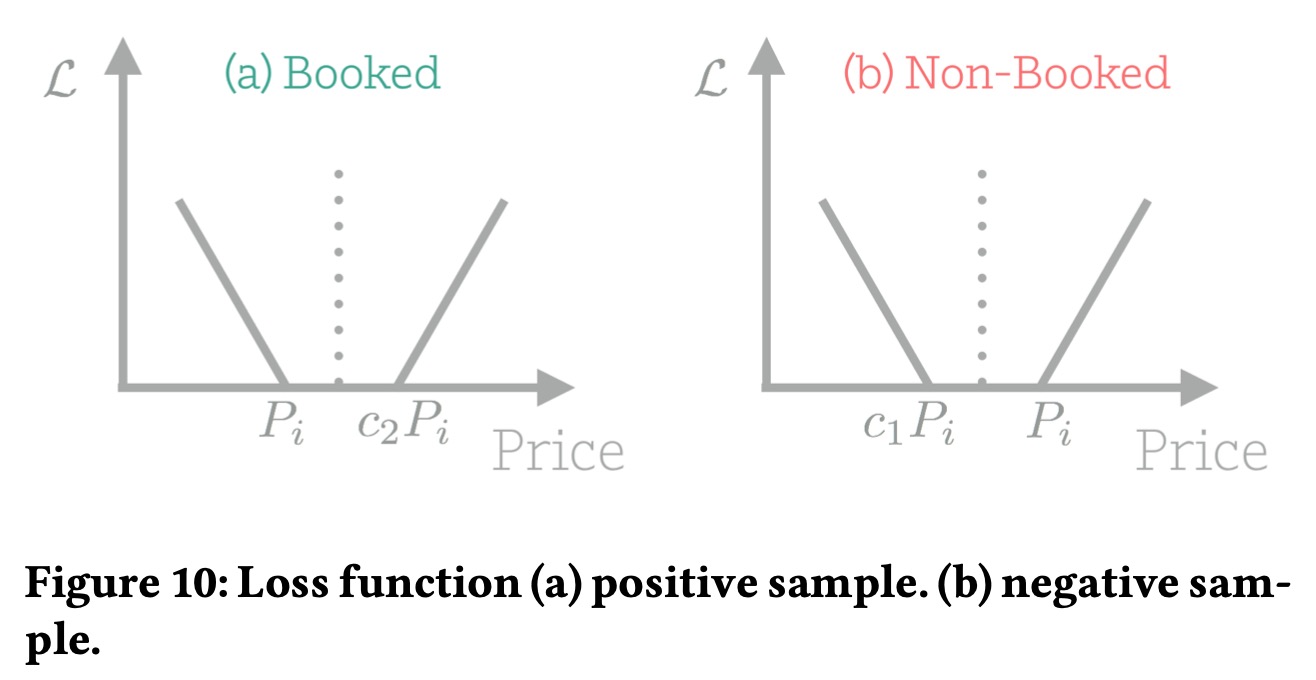
loss function

如果\(c_1=c_2=1\)，则\(L=U\), 最优推荐价格就是当前价格，可以选择合适的\(c_1\)和\(c_2\)来确定价格变化范围。

上面我们描述了这个模型loss是什么，下面我们讲一下特殊的函数形式，将输入特征映射到建议价格上，这个函数需要满足几个假设：

  • 对于同样的房价，建议价格与预测预定概率是正相关的，这使得我的建议价格是随着预定概率变化的
  • 建议价格需要在房东预设的价格附近
  • 额外的未被预定概率模型包含的需求信息需要容易加入

基于以上几个假设，我们引入模型 \[ \begin{aligned} P_{sug}&=P \cdot V \\ V &= \begin{cases} 1+\theta_1(q^{\psi_H^{-qD}}-\theta_2) & \text{if} \quad D>0 \\ 1+\theta_1(q^{\psi_L^{-(1-q)D}}-\theta_2) & \text{if} \quad D\leq0 \\ \end{cases} \end{aligned} \] 这里\(P\)表示房东原先设定的价格，\(q\)表示在价格\(P\)下的预估预定概率，\(D\)是需求分数（从额外的需求信息中获得），一些相似的房间会被聚合成一个组。在上式中，\(\theta_1\)控制价格增加或者降低幅度，\(\theta_2\)用于当推荐价格一致时调整的参数，这样当给定\(\theta_1\)和\(\theta_2\)时，\(P_{sug}\)对于预定概率\(q\)时单调递增的，这使得我们可以在房间有较高预定概率的时候涨价。

需求分数\(D\)是在分组上高斯标准化的，这个值越高表明需求越高，需求常数\(1<\psi_L<\psi_H<2\)可以用来控制需求函数的形状。

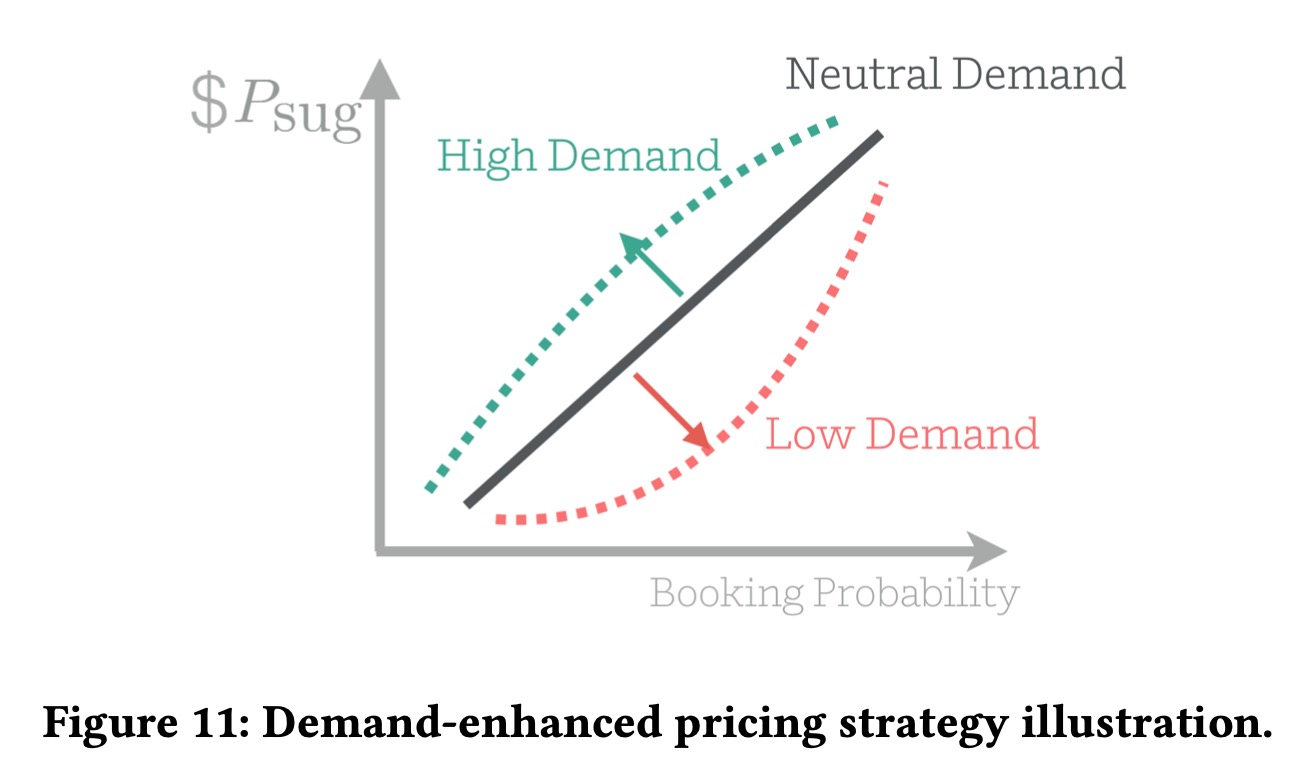
book p & P_sug

其中\(\theta_1\)和\(\theta_2\)是房间粒度训练得到的，一般梯度下降进行学习。

训练过程：

  • 房间粒度的建模，因为即使是相同地区的房价价格也会有比较大的变化，所以我们为400w+的房间分别建模，同时我们也会保留市场粒度或者全局粒度的模型，来做候选。

  • 模型参数约束，我们会定一些上下限制的约束来保证给出的价格建议不会过于离谱。

  • 随机梯度下降，用spark来做并行训练以及模型更新（有约束的优化）

  • 训练数据，airbnb会受到季节等周期性的影响，所以训练上会更多关注于最近的预约行为。与预约概率模型会采用过去一年的数据不同，策略模型会采用未来所有预约的样本以及过去一周预约的样本。

EXPERIMENTS

离线评估，在离线评估中，关注于某段时间内的正负例样本

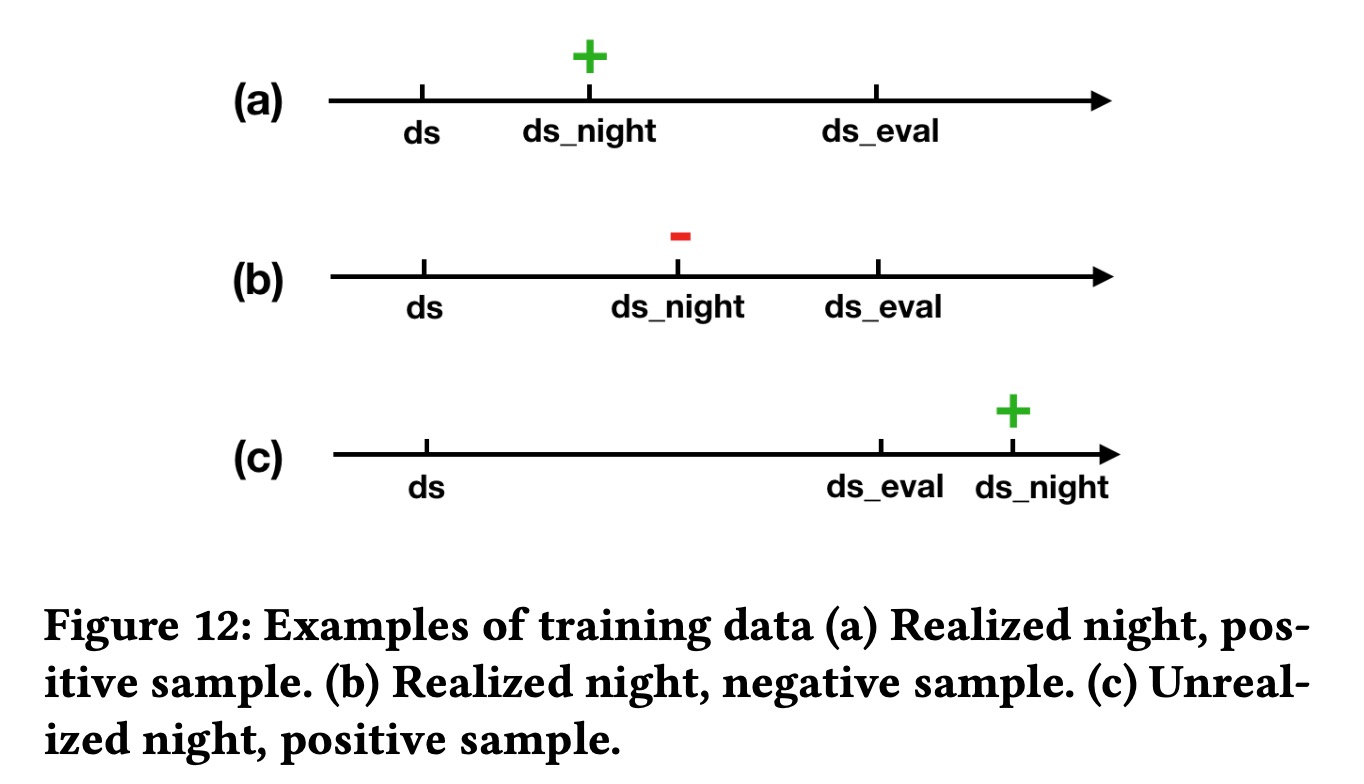
traning samples

随机选了几段时间（分别为abc），10%的房间作为评估。

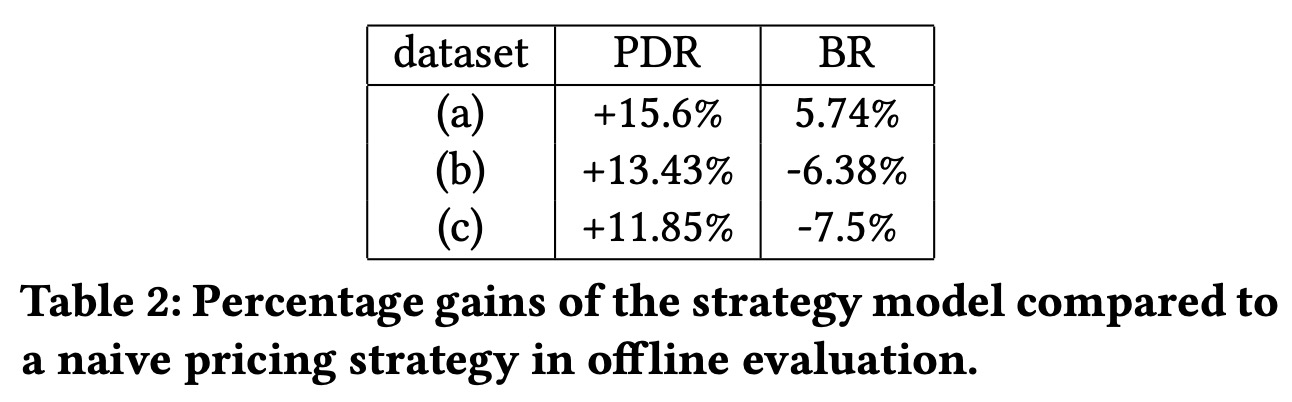
offline evaluation

线上评估，文中只说上线取得了较大的收益，同时离线指标的提出也帮助了后面的迭代。