定价相关文章三连,第二篇,这篇是美国某航空咨询公司发表的一篇航旅附加产品定价的文章,主要思路与airbnb的较为一致,但是业务场景会有些差别,中了kdd2019。
Introduction
在航旅行业中,附加产品(Ancillariey,不知道怎么翻译)已经是提升收益和利润的主要来源,传统的定价策略只是基于商业规则来制定的,并没有根据市场的变化进行改变。这篇文章描述了一个第三方航旅咨询提供的动态定价模型,通过定价模型来为用户提供推荐价格,优化提高客均受益。在这篇文章中描述了三种动态定价的方式:
- 两阶段的预测和优化模型
- 两阶段的模型,使用dnn来预测,同时做离散最优价格搜索
- 一阶段端到端的dnn模型来推荐最优价格。
现在主要的用户session状态如下图所示
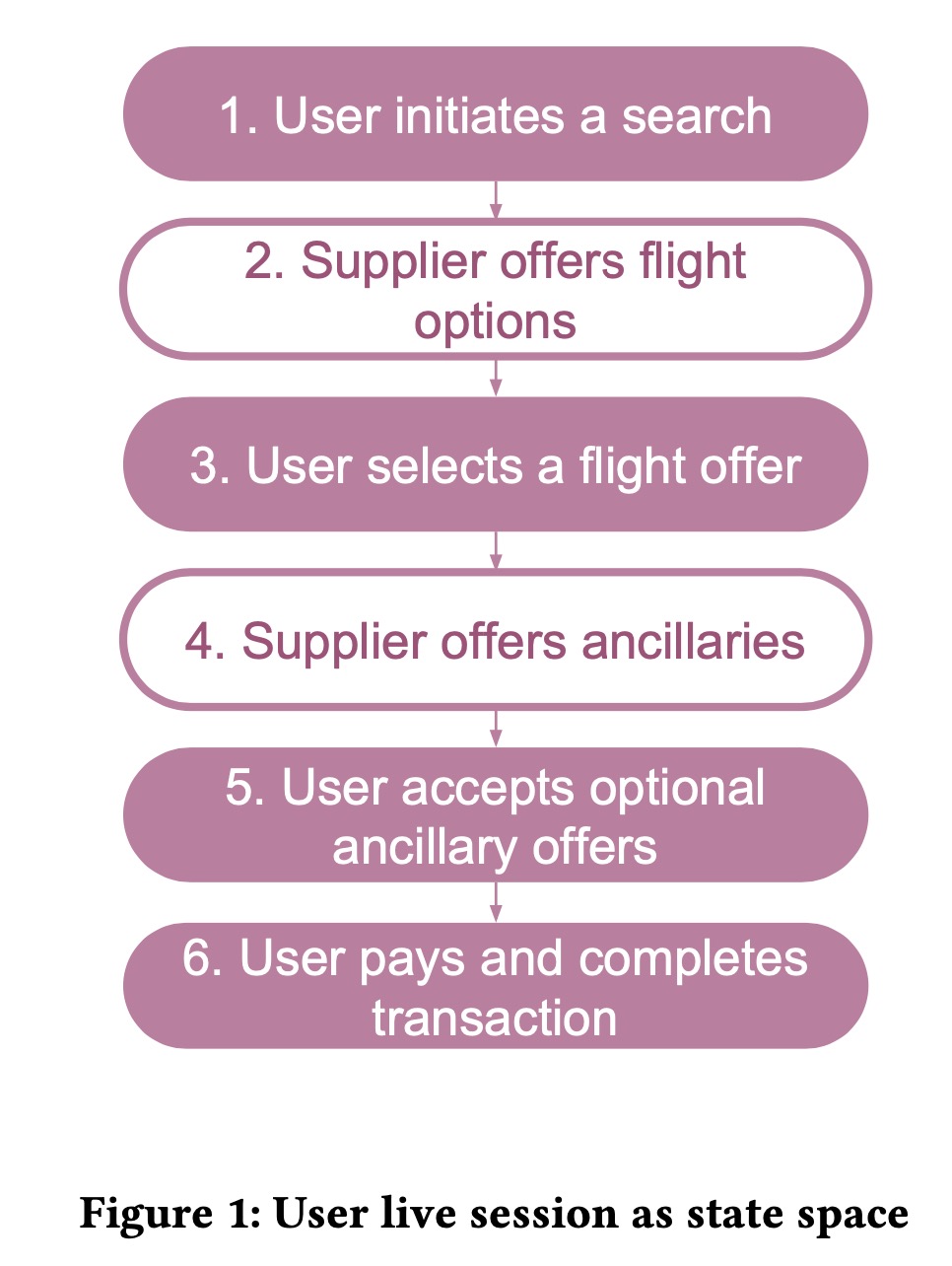
用户到来后进行搜索,航旅供应商提供满足条件的航班,用户选择其中一个,航旅供应商提供附加产品,用户接受,用户付费。本篇文章主要目标就是动态优化价格,估计用户的付费意愿。主要的contribution包括:
- 提供一个丰富、定制化的动态价格推荐系统
- 开发了一个深度模型,估计购买概率,同时根据建模用户的购买意愿的单调性质来制定价格
- 相比于baseline model表现更好,预估更准确
- 在实际数据上测试模型,并在离线、在线的指标上都有所提升
Pricing Factors
定义需求曲线\(D(P)\)是价格\(P\)的函数,最优价格可以通过最大化期望收益得到\(P^*=\underset{P}{\arg\max} P \times D(P)\)。对于航空行业,需求函数并不只是价格的函数,还包括用户的属性。
我们定义用户的属性\(\bf{x}\)是一系列因素的集合,包括时间、市场状况以及停留时间等等。
- 时间因素主要包括距离出发的天数以及出发的日期时间,对于前者我们发现购买时间越早的人群对于价格越敏感,对于后者更方便出发的时段或者节日、事件都会影响最后结果。
- 市场状况主要是航班的起终点,我们会将客户映射到某个起终点对的聚类上,来表征用户所在的市场环境

- 停留时长,LOS,客户在目的地停留时长,购买附加产品的用户停留时长的分布会高于整体的均值

Pricing Model
定价模型由两部分组成:
- 附加品的购买概率(二分类问题)
- 收益优化模型,给定购买概率和推荐的价格,最大化期望收益。
两个假设:
- 价格区间,由商业规则制定的,相对合理的价格区间
- 支付意愿的单调性,如果用户以价格\(p\)购买了产品,对于任意价格\(p'<p\),用户都会愿意支付,用户在价格\(p\)时没有购买产品,对于任意价格\(p'>p\),用户都不会愿意购买。
实现了三种不同复杂度的定价模型
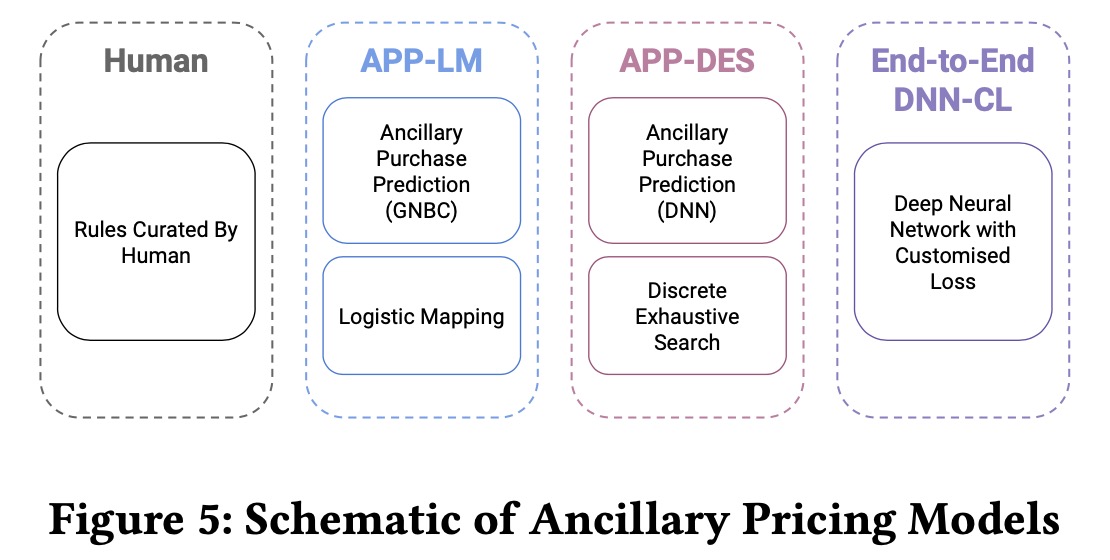
Ancillary Purchase Probability Model
对每一个sub-market(也就是起终点对聚类)建立附加产品的购买概率模型,作为需求曲线。采用30+特征:

我们对比了多种不同的模型,用AUC来进行评估(因为存在样本不均衡问题)
收益优化
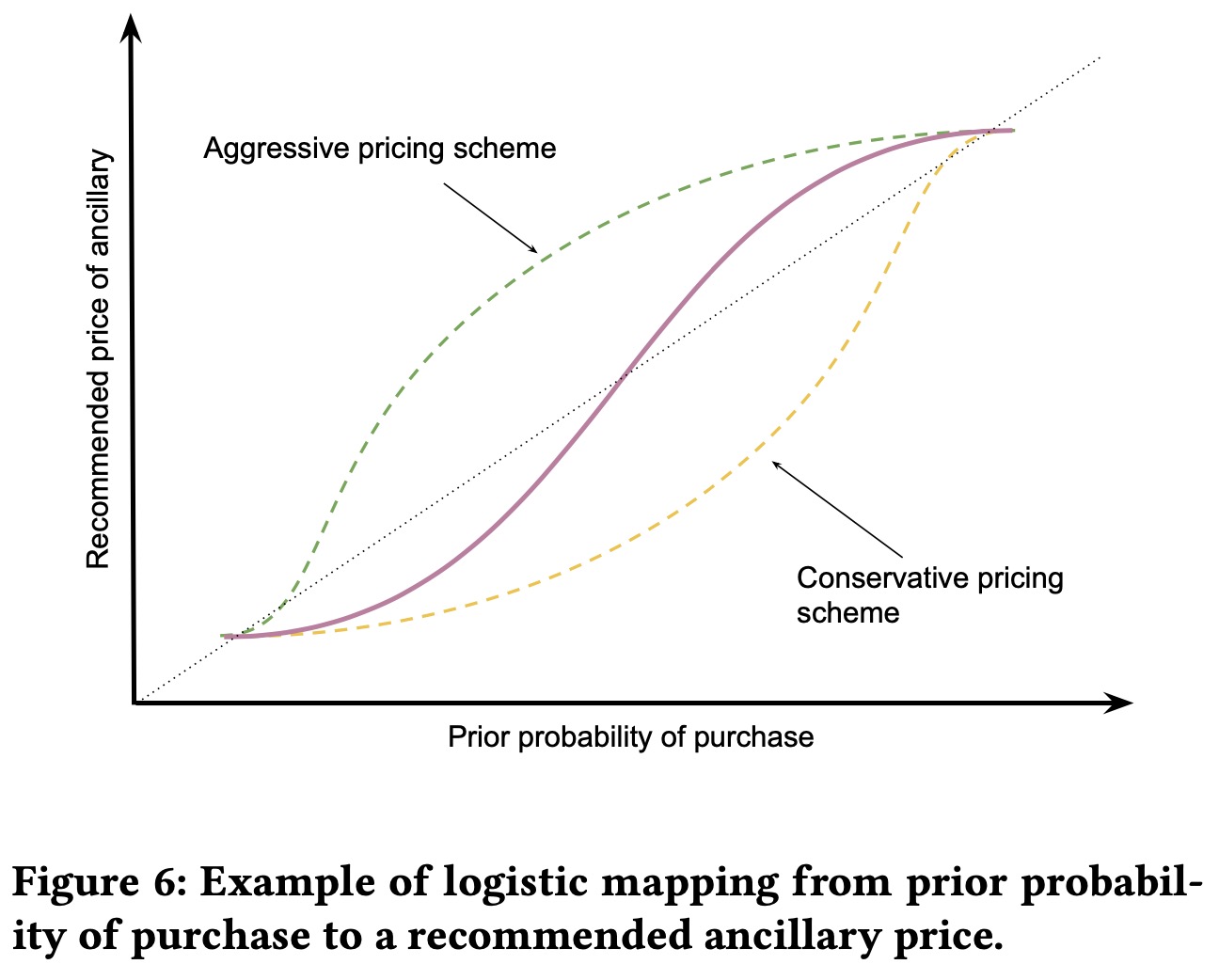
在我们的基线模型APP-LM中,我们用一个logistic函数将购买概率映射到推荐价格上,这样做是因为我们希望购买概率高的附加产品对他们定更高的价格,概率低的定较低的价格 \[ p^{rec} = \frac{L}{1+\exp^-k(x-x_0)} \] 其中\(L\)表示原价,形状参数\(k\),中间点参数\(x_0\),通过调整参数我们可以有不同的定价策略,比如说激进的或者是保守的。
除了上面这种方式,我们也可以将金额进行离散化处理后,进行便利搜索,然后寻找受益最大的,这种方式被称为Discrete Exhaustive Search。
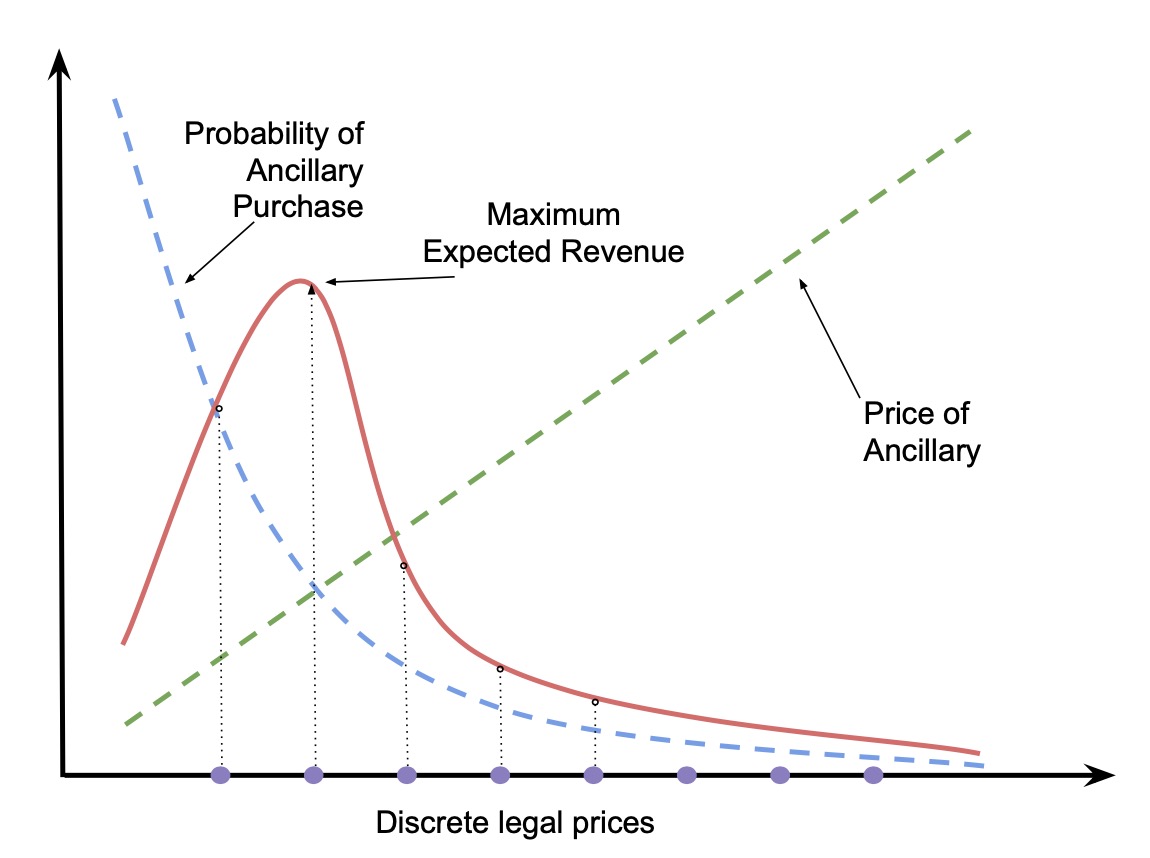
这样两阶段的预测+优化方法,对于需求预测的准确性要求比较高,而预测的准确性依赖于历史上这样的价格出现的数量。(此处是重点)
定制Loss的DNN-CL模型
我们提出一种定制化的loss,同时考虑了定价过低被购买以及定价过高未售出的regret,这个loss的设计思路跟airbnb的差不太多,通过增加潜在变量的方式,来考虑支付意愿的单调性性质。 \[ \begin{aligned} \mathcal{L}&=\underset{\theta}{\arg\in} \sum_{i=1}^N\sum_{j=1}^{|\mathbb{F}|} (\Phi_{lb}+\Phi_{ub})\cdot \mathbb{I}_{\sigma_{ij}>0} \\ \Phi_{lb} &=\max\bigg(0, \big(L(P_{ij},\delta_{ij})- \mathbb{F}_{\Theta}({\bf{x}}_i, \mathbb{F}) \big) \bigg)\\ \Phi_{ub} &=\max\bigg(0, \mathbb{F}_{\Theta}({\bf{x}}_i, \mathbb{F}) \big) - \big(U(P_{ij},\delta_{ij}) \bigg)\\ \end{aligned} \] 其中\(\delta_{ij}\)如下图所示
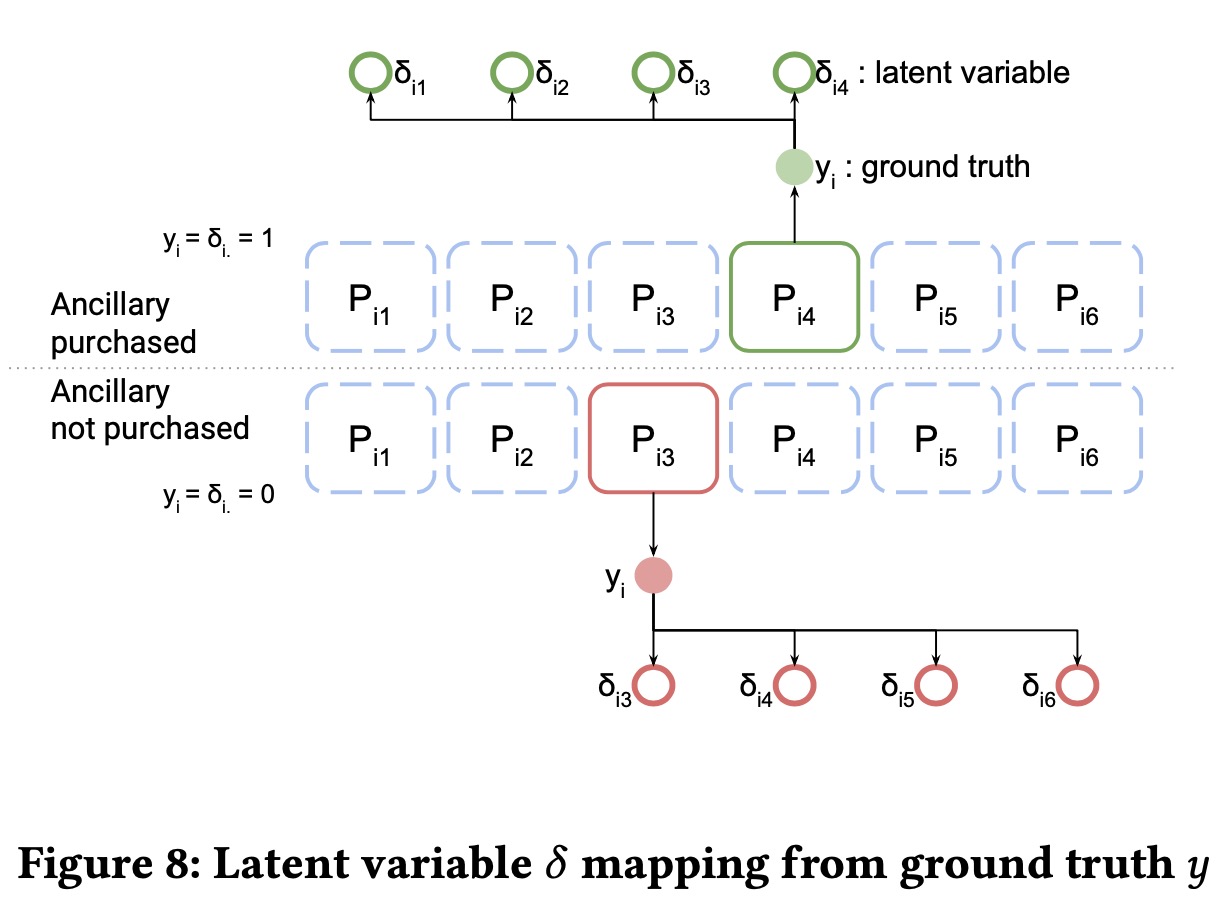
其中\(\sigma_{ij}=(j-j^*)\cdot(-1)^{y_i}\)。定义下限和上限函数 \[ \begin{aligned} L(P_{ij},\delta_{ij})=\delta_{ij}\cdot P_{ij}+(1-\delta_{ij})\cdot c_1P_{ij}\\ U(P_{ij},\delta_{ij})=(1-\delta_{ij})\cdot P_{ij}+\delta_{ij}\cdot c_1P_{ij} \end{aligned} \] 其中\(c_1\)和\(c_2\)用来调整合适的价格。

Evaluation
离线指标:
- 采用Price Decrease Recall (PDR) and Price Decrease Precision (PDP),前者表现了对于未购买的商品,我们推荐的价格会低于当前价格的概率,后者表现了未购买的善品中我们推荐价格低于当前价格的百分比
- 注AUC,相当于给定价格下的二分类问题预测值的好坏
- RS,\(\text{RS}=\underset{\text{purchases}}{\text{mean}}\big(\max(0,1-\frac{p^\text{rec}}{p}\big)\),衡量了推荐价格和真实价格的接近程度
- Price Decrease F1 (PDF1),\(\text{PDF1}=\frac{2\cdot \text{PDR}\cdot \text{PDDP}}{\text{PDR}+\text{PDDP}}\)
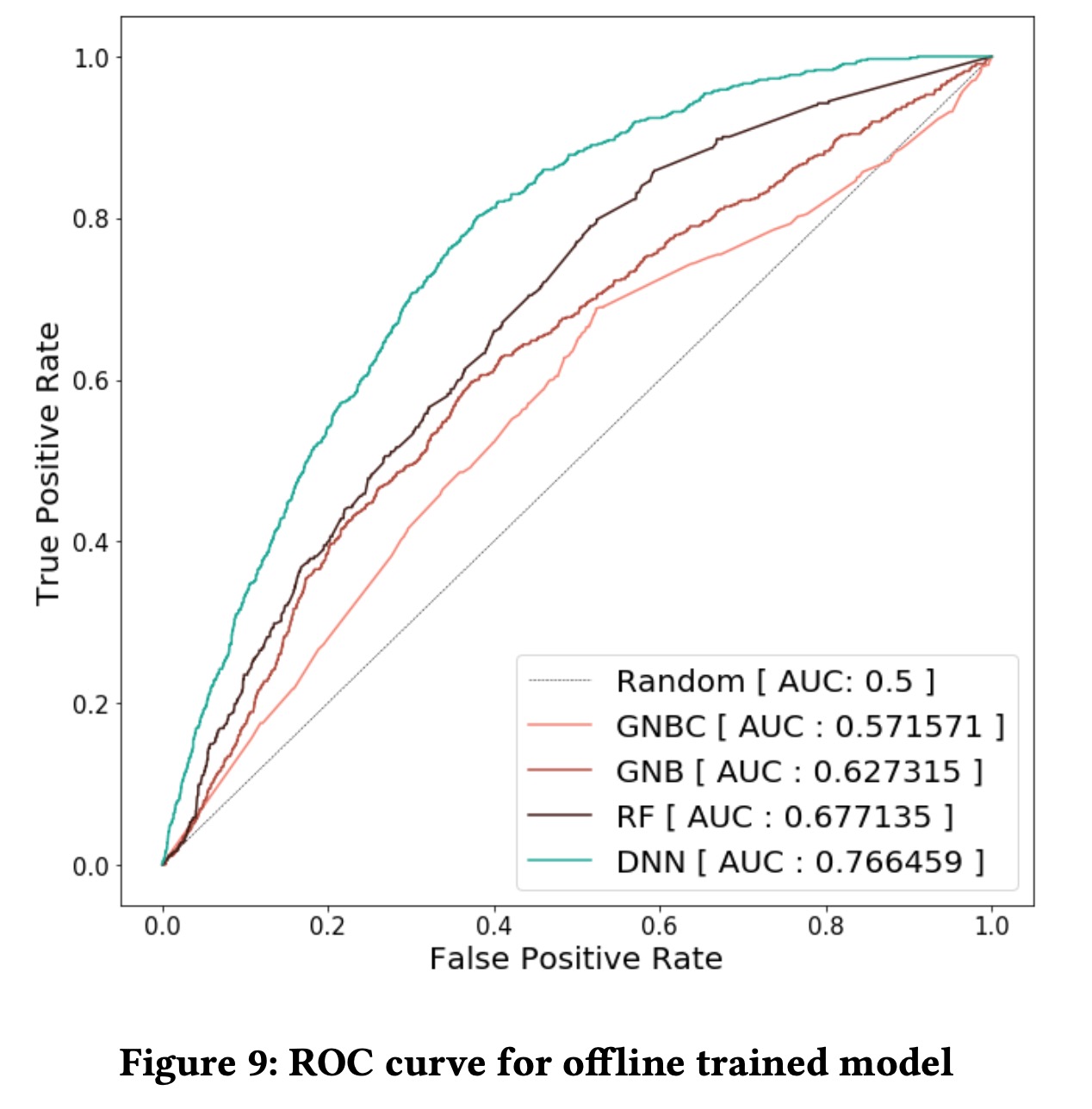
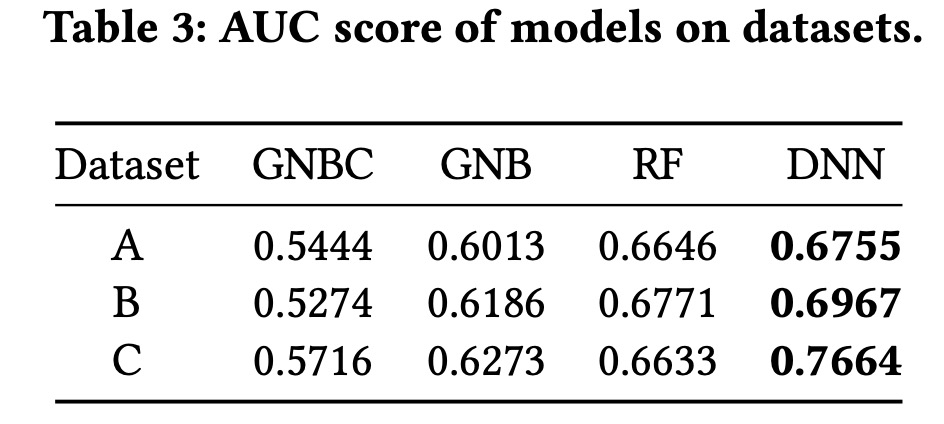
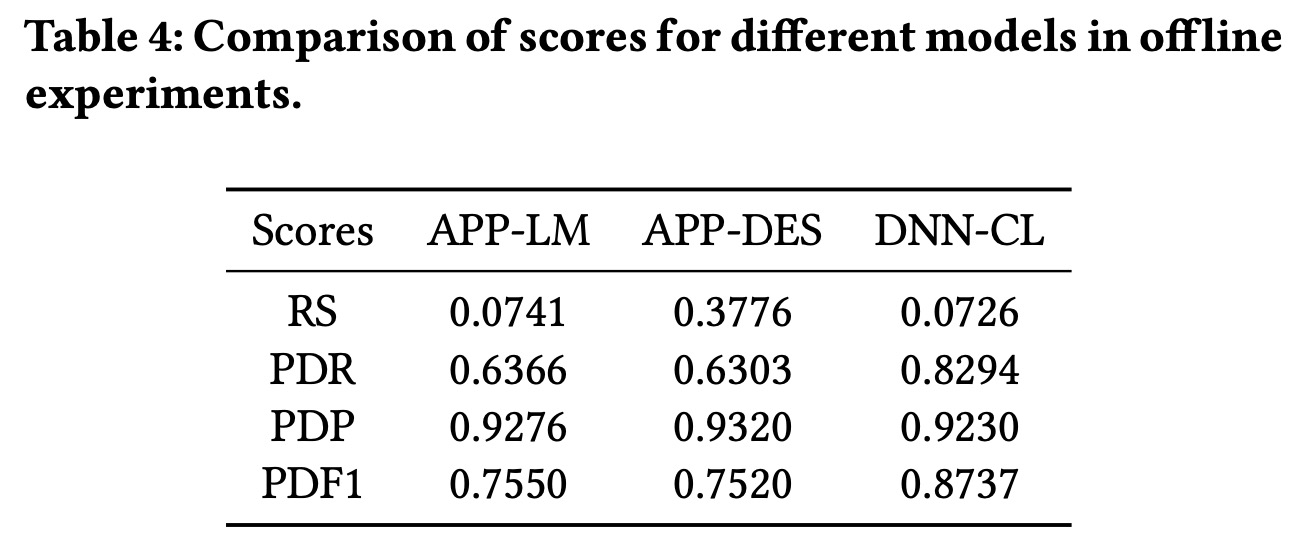
这边离线结果有个比较有意思的现象,接入DNN的模型之后,AUC指标明显上升,但是对于最终推荐价格相关的指标而言,效果并不好,这说明APP-DES模型可以在第一阶段二分类问题上拟合到比较好的相关性,但是却错误估计了价格和需求之间的关系。
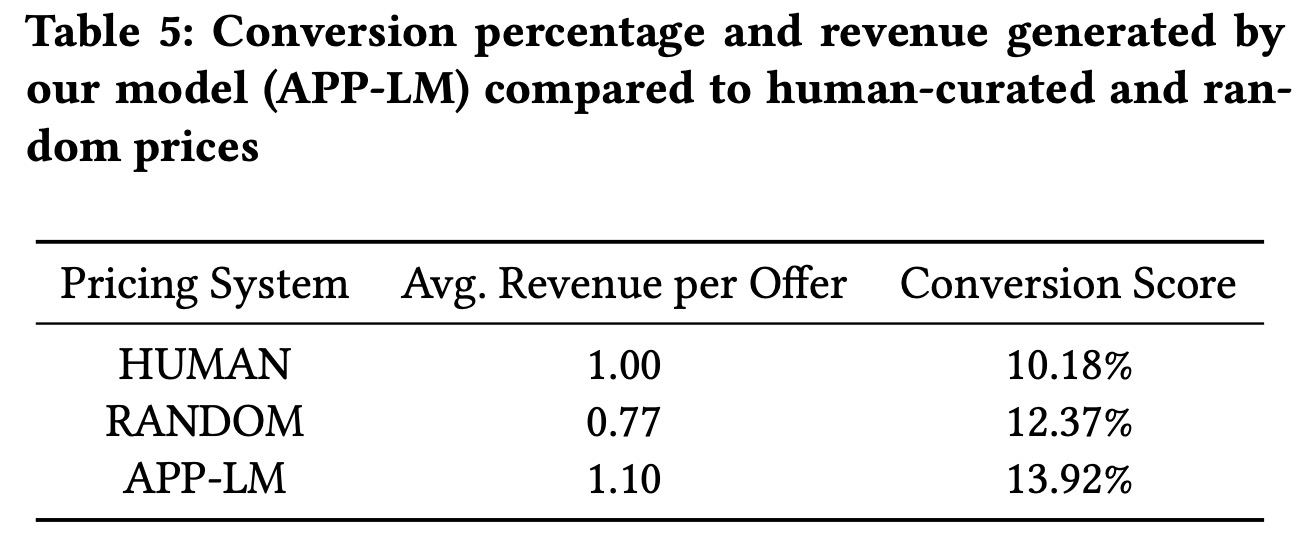
在线指标
- 转化率
- 单个订单(session)平均收益
在实际应用时候,我们在APP-LM模型上增加一个随机折扣模型,这个随机折扣可以在推荐的价格附近上下浮动,这么做有两个原因:
- 建立一个转化率的baseline,在此基础上进行价格优化
- 这使得我们可以拥有更多价格变化范围更大的训练数据