闲话Variable Selection和Lasso

最近在看变量选择（也叫subset selection），然后来总结一下，想到哪写到哪的随意风格（手动微笑）。[11,12,13]是主要参考的综述文章。

Boosting 和 Stagewise Regression

嗯，我也很惊讶为什么这个Lasso会跟Boosting挂着勾。Lasso这样的带罚项的regression最早的思想来自于linear regression boosting，传统的boosting是只对残差进行boosting，然后对true function进行fitting，Incremental Forward Stagewise 则是依次选择跟残差最相关的特征（记得做归一化，血的教训带来的微笑），然后boosting，再某种条件下停止，达到选择特征同时对regression做shrinkage的目的。

与之很相似的是Forward Stepwiese Regression，一个是stepwise，一个是stagewise，stepwise在选择的时候依次直接加入，做fitting，而不是做residual boosting。但是Forward Stepwiese Regression是不稳定的，数据的微小改变会使变量的选择改变，之后选择的变量也会不同，最后选择的变量子集也会完全不同。一种变形是反向的Backward Stepwise Regression，先做全部变量的回归，然后依次拿掉变量。这两种算法都采用的贪婪策略，在每一步选择最优的改变，却无视特征的影响，所以不如stagewise。

Lasso

最常见的一种Lasso，最早在[1]中提出，常见的正态分布残差假设的线性回归模型写作

\[ y=X\beta+\epsilon \]

通过最小化残差平方和得到最优拟合，考虑L1的约束

\[ \begin{aligned} \hat{\beta}=\underset{\beta}{\arg\min}\|y-X\beta\|^2_2 &&\text{s.t. }\|\beta\|_1\leq s \end{aligned} \]

也可以用拉格朗日形式

\[ \hat{\beta}=\underset{\beta}{\arg\min}\|y-X\beta\|^2_2+\lambda\|\beta\|_1 \]

这样写出来的优化问题虽然是凸的，但不可导，无法直接求解，给定有限的样本，通常可以得到有偏的估计，也称作正则化的估计。

通常求解Lasso都是通过soft-thresholding，来进行一个阶段

\[ \hat{\beta_j}=\text{sign}(\hat{\beta_j^{\text{ls}}})(\hat{\beta_j^{\text{ls}}}- \lambda)_+,j\in{1,\cdots,p} \]

其中\(\hat{\beta_j^{\text{ls}}}\)表示第\(j\)个变量的最小二乘估计，\((\cdot)_+\)表示取正数部分，与之相似的是加了L2正则的ridge regression的解为

\[ \hat{\beta_j}=\hat{\beta_j^{\text{ls}}}/(1+\lambda),j\in{1,\cdots,p} \]

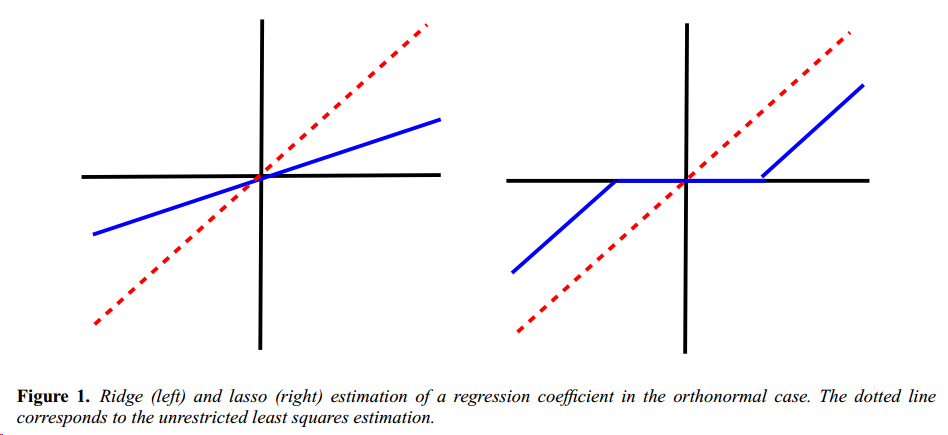
当回归的维数\(p\)大于样本数量\(N\)时，Lasso可以有效选择出有用的变量并且得到较好的回归效果。

自由度（df）对于调节参数\(\lambda\)的大小通常也很有用，常用的包括Akaike Information Criterion（AIC）和Bayesian Information Criterion（BIC），他们将模型的自由度也作为评判模型好坏的标准，AIC就定义为

\[ \text{AIC}=\log\|\hat{y}-y\|^2_2+2\text{df} \]

这里提一下，AIC和BIC标准定义如下：

\[ \begin{aligned} \text{AIC}=2k-2\ln(\hat{L})\\ \text{BIC}=\ln(n)k-2\ln(\hat{L}) \end{aligned} \]

其中\(\hat{L}\)是最大似然函数，\(n\)是观测数据样本数量，\(k\)是模型中估计的参数，残差服从正态分布的时候就可以写成上面的形式。

尽管AIC关注于最小误差，关注BIC可以得到更加稀疏的模型。通常lasso估计的自由度可以用非零系数个数来表示，通过shrinking系数，来削减模型的自由度，这样我们可以选择一些变量同时丢弃一些变量，但要注意这只适用于\(p<N\)的情况，当\(X\)是否满秩不可知时，也同样不适用。

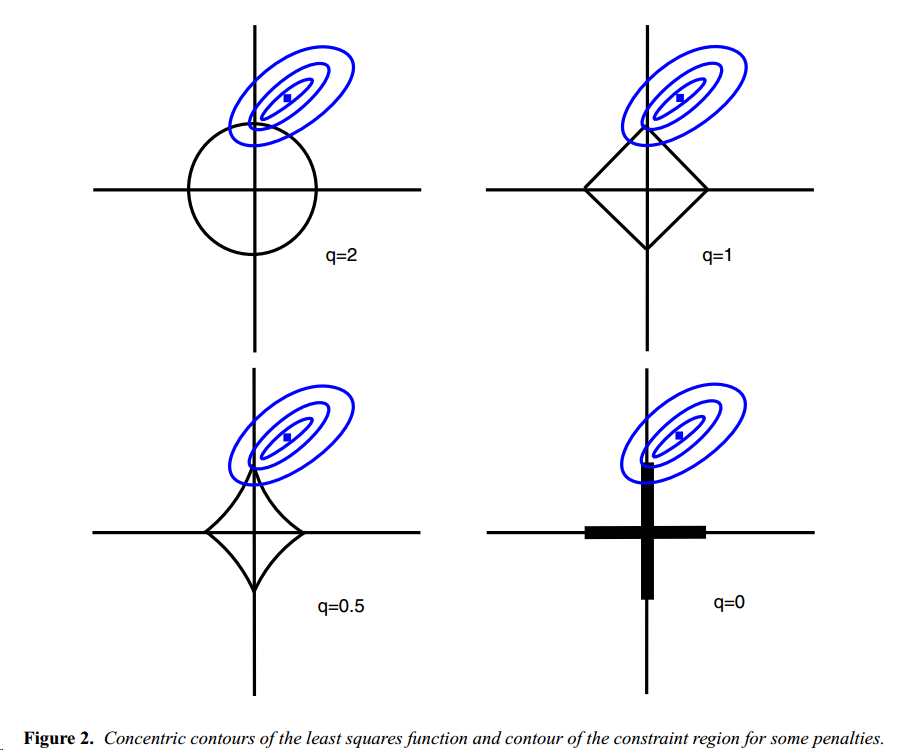
对于正则项\(\|\cdot\|^q_q\)的选择，当\(q\leq 1\)的时候，可以达到变量缩减的目的。

目前Lasso的主流实现一般用二次规划，同时当\(p>n\)的时候最多选择\(n-1\)个变量，这个由凸对偶性保证（只是看到，未经深究）。

lasso和robust regression

lasso某种程度上也是一种鲁棒性回归，

\[ \hat{\beta}=\underset{\beta}{\arg\min}\{\max_{z\in\theta}\|y-(X+Z)\beta\|_2\} \]

其中\(Z\)是一个disturbance的矩阵，\(\theta\)称为uncertainty set，lasso可以看做是有特殊不确定集的robust regression的求解。

LAR

最小角回归（Least Angle Regression）[2]是今年比较流行的一种求解Lasso的方式，也是LAR出现之后，Lasso才被逐渐重视起来，主要思想是，经过归一化后，选择与\(y\)最相关的变量\(\beta_j\)加入（也就是加入第\(j\)个特征），然后增加\(\beta_j\)直至另一个变量比它俩更相关，重复此过程，直至没有变量与\(y\)相关或者函数足够拟合。

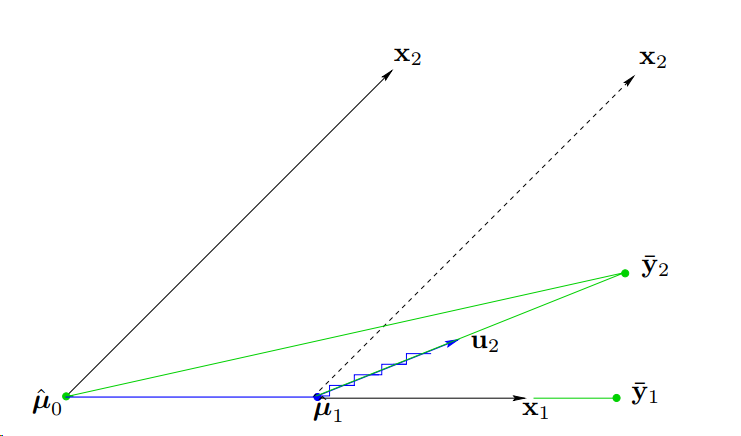
与之前的几种方式相比，LAR不用在第一步时候前进多步（boosting会有衰减\(\epsilon\)），而是直接到达合适位置直到第二个变量加入模型，也不用在多个变量之间迭代多步，而是在第三个变量加入模型前直接到达合适的点，下图就可以很好地说明

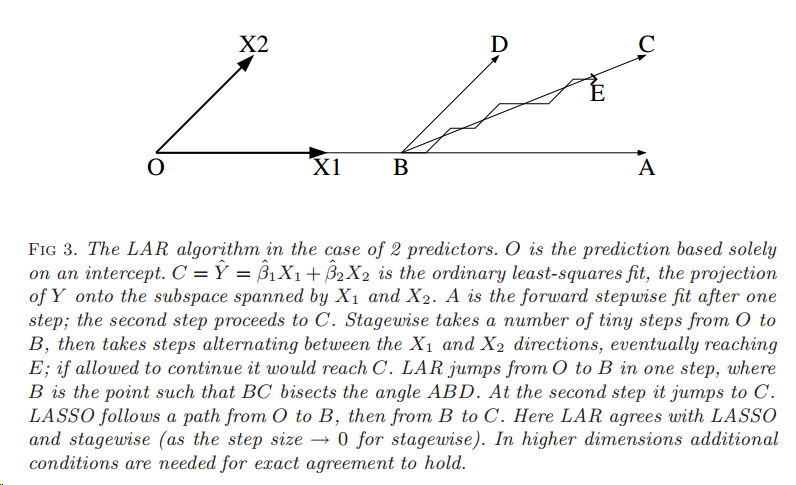
Stepwise的方式是O->A->C，Stagewise的方式是O->B->E->C，注意其中O->B和B->E都是多步尝试后到达，LAR则是O->B->C，都是选择很合适的位置，其中BC平分角DBA，因为LAR选择时会在BA，BD同样相关的情况（LAR选择策略，一个step前进至两个变量和预测值具有相同相关性的位置）。以上都是在比较理想的情况，大部分高维的情况下都需要满足一定条件才会收敛。

LAR有几个比较remarkable的性质：

速度快，当\(p < n\)时，需要\(O(p^3+np^2)\)次最小二乘拟合的计算
可以用于拟合Lasso和stagewise模型
可以使用简单的统计标准来选择步数，如\(C_p\)

\[ C_p=(1/\hat{sigma}^2)\sum^n_{i=1}(y_i-\hat{y_i})^2-n+2k \]

其中\(k\)是步数，\(\hat{sigma}^2\)是估计残差的方差，\(C_p\)提供了一种简单的停止算法的规则。

Pathwise coordinate descent for lasso

[3, 4]中提到利用坐标下降的方式求解Lasso，求解lasso的原问题等价于求解

\[ \min_\beta\frac{1}{2}(\beta-\hat{\beta})^2+\gamma|\beta| \]

其中\(\hat{\beta}=\sum_ix_iy_i\)，是最小二乘系数，如果\(\beta>0\)时我们求偏导有

\[ \frac{df}{d\beta}=\beta-\hat{\beta}+\gamma=0 \]

此时我们就有soft-threshold的结果

\[ \begin{aligned} \hat{\beta}^{\text{lasso}}(\gamma)&=S(\hat{\beta},\gamma)=sign(\hat{\beta})(|\hat{\beta}|-\gamma)_+ \\ &=\begin{cases} \hat{\beta}-\gamma,&&\hat{\beta}>0, \gamma<|\hat{\beta}|\\ \hat{\beta}+\gamma,&&\hat{\beta}<0, \gamma<|\hat{\beta}|\\ 0,&&\gamma>|\hat{\beta}|\\ \end{cases} \end{aligned} \]

考虑用迭代的方式来依次计算每一个变量

\[ f(\tilde{\beta})=\frac{1}{2}\sum^n_{i=1}(y_i-\sum_{k\neq j}x_{ik}\tilde{\beta}_k-x_ij\beta_j)^2+\gamma\sum{k\neq j}|\tilde{\beta}_j|+gamma|\beta_j| \]

通过最小化每个变量

\[ \tilde{\gamma}\leftarrow S(\sum^n_{i=1}x_{ij}(y_i-\tilde{y}_i^{(j)}),\gamma) \]

多步迭代后收敛。这样相比于其他做lasso的方式而言，当变量个数增加时更加有高效，同时每个解都可以作为下一个变量求解的warm start。

Lasso的贝叶斯解释

我们可以将最小二乘解释为无参数分布先验时最大化后验概率估计的问题，Lasso可以视为Laplace先验或者是双指数分布先验，对于参数\(\beta\)，Laplace先验为

\[ \pi(\beta|\sigma^2)=\prod_{j=1}^{p}\frac{\lambda}{2\sigma}\exp\frac{-\lambda|\beta_j|}{\sigma} \]

所以我们可以用Gibbs采样或者EM算法来做inference求解。

Lasso改进

任何形式的正则都会给估计值带来bias，同时很大程度降低了方差，另外，当真正的非零系数非常少，lasso会对正确的变量系数产生有偏估计。为了降低bias，[5]中提出一种relaxed lasso，进行两阶段的估计，首先用lasso得到一些稀疏的变量，然后用低一些的正则系数来估计选择的变量，因此我们每一步都需要选择合适的regularization parameters，所以每步都需要进行cross-validation这样的方式来选择参数。

基于这种relaxed lasso，[6]提出Variable Inclusion and Shrinkage Algorithm（VISA）的模型，在第二步中VISA并不忽略之前已经忽略的变量，而是给选择的变量更高的优先级。

[7] 提出一种adaptive lasso，给每个变量不同的重要性

\[ \hat{\beta}=\underset{\beta}{\arg\min}\|y-X\beta\|^2_2+\lambda\sum_{j=1}^{p}w_j|\beta_j| \]

当\(N\geq p\)时，权重计算为

\[ w_j=\frac{1}{|\hat{\beta}_j^{\text{ls}}|^\gamma},\gamma\geq 0 \]

当\(N < p\)时，权重通过计算最小二乘估计时的最小正则项得到。[7]中表明adaptive lasso在变量选择方面，比其他lasso模型更优。

[8]里面提出elastic net，同时结合了L1和L2正则项

\[ \hat{\beta}=\underset{\beta}{\arg\min}\|y-X\beta\|^2_2+\lambda(\alpha\|\beta\|_1+(1-\alpha)\|\beta\|_2^2) \]

除了在有correlated predictors上有较Lasso相比更好的表现，当\(p>N\)的时候，Lasso最多只能选出\(N\)个预测值，但是elastic net可以选择超过\(N\)个预测值。当我们有group of relevant and redundant的变量时，Lasso通常只会从中选取一个并且忽略其他的，elastic net则会选择全部，同时平衡它们的参数估计值。

也有人考虑通过下采样的方式来增加稳定性和模型选择的准确度，所以称之为bolasso[9,10]

Other Methods

除了上面提到的还有SCAD[14]、Dantzig selector[15]及其衍生算法等，并没有仔细研究过，就不误人子弟了。

后话

最近用到的大概是一个变量选择，我最开始考虑的是用RF做OOB，但是这次的特征有很多具有共线性，并没有找到RF对共线特征的表现，然后考虑lasso的方式，同时也关注这些模型对于共线性的鲁棒性，也是最近看到的ADL模型通常用到的，主要考虑了sklearn的lasso和lar，动手验证了一下，lar对于共线性的鲁棒性很好，相比之下lasso就差了很多，看了一下实现，发现lasso和ridge都是基于elastic net做coordinate descent，只不过设置\(\alpha\)的值而已。

突然想到一种用resampling验证的方式，用bootstrap等方法做出RMSE的经验分布，然后拿掉个别变量，看分布变化，如果显著不同且降低，则可以去掉变量。

Reference

[1] Tibshirani, R. (1996). Regression Shrinkage and Selection via the Lasso. J. Roy. Stat. Soc. Ser. B, 58(1), 267–288.

[2] Efron, B., Johnstone, I., Hastie, T. & Tibshirani, R. (2004). Least Angle Regression. Ann. Statist., 32(2), 407–499

[3] Friedman, Jerome, et al. "Pathwise coordinate optimization." The Annals of Applied Statistics 1.2 (2007): 302-332.

[4] Wu, Tong Tong, and Kenneth Lange. "Coordinate descent algorithms for lasso penalized regression." The Annals of Applied Statistics 2.1 (2008): 224-244.

[5] Meinshausen, N. (2007). Lasso with Relaxation. Comput. Stat. Data Anal., 52(1), 374–393.

[6] Radchenko, P. & James, G. M. (2008). Variable Inclusion and Shrinkage Algorithms. J. Amer. Statist. Assoc., 103(483), 1304–1315.

[7] Zou, H. (2006). The Adaptive Lasso and Its Oracle Properties. J. Amer. Statist. Assoc., 101(12), 1418–1429.

[8] Zou, H. & Hastie, T. (2005). Regularization and Variable Selection via the Elastic Net. J. Roy. Stat. Soc. Ser. B, 67(2), 301–320

[9] Bach, F. R. (2008a). Bolasso: Model Consistent Lasso Estimation Through the Bootstrap. 15th International Conference on Machine Learning; 33–40.

[10] Chatterjee, A. & Lahiri, S. N. (2011). Bootstrapping Lasso Estimators. J. Amer. Statist. Assoc., 106(494), 608–625.

[11] Vidaurre, Diego, Concha Bielza, and Pedro Larrañaga. "A survey of L1 regression." International Statistical Review 81.3 (2013): 361-387.

[12] Tibshirani, Robert. "Regression shrinkage and selection via the lasso: a retrospective." Journal of the Royal Statistical Society: Series B (Statistical Methodology) 73.3 (2011): 273-282.

[13] Hesterberg, Tim, et al. "Least angle and ℓ1 penalized regression: A review." Statistics Surveys 2 (2008): 61-93.

[14] Fan, Jianqing, and Runze Li. "Variable selection via nonconcave penalized likelihood and its oracle properties." Journal of the American statistical Association 96.456 (2001): 1348-1360.

[15] Candes, Emmanuel, and Terence Tao. "The Dantzig selector: Statistical estimation when p is much larger than n." The Annals of Statistics 35.6 (2007): 2313-2351.