A Unified Solution to Constrained Bidding in Online Display Advertising

发表于 | 分类于

TL;DR

本文提出一种通用的智能出价框架，可以满足不同广告主关于竞价目标和约束的诉求，具体出价调控算法的实现为DDPG，目前该算法已经在淘宝广告平台部署使用。

Abstract

In online display advertising, advertisers usually participate in real- time bidding to acquire ad impression opportunities. In most advertising platforms, a typical impression acquiring demand of advertisers is to maximize the sum value of winning impressions under budget and some key performance indicators constraints, (e.g. maximizing clicks with the constraints of budget and cost per click upper bound). The demand can be various in value type (e.g. ad exposure/click), constraint type (e.g. cost per unit value) and con- straint number. Existing works usually focus on a specific demand or hardly achieve the optimum. In this paper, we formulate the demand as a constrained bidding problem, and deduce a unified optimal bidding function on behalf of an advertiser. The optimal bidding function facilitates an advertiser calculating bids for all impressions with only 𝑚 parameters, where 𝑚 is the constraint number. However, in real application, it is non-trivial to determine the parameters due to the non-stationary auction environment. We further propose a reinforcement learning (RL) method to dynam- ically adjust parameters to achieve the optimum, whose converging efficiency is significantly boosted by the recursive optimiza- tion property in our formulation. We name the formulation and the RL method, together, as Unified Solution to Constrained Bid- ding (USCB). USCB is verified to be effective on industrial datasets and is deployed in Alibaba display advertising platform.

在在线展示广告中，广告主通常参与实时竞价来获取广告曝光机会。在大多数广告平台上，广告主获取曝光的需求是在 预算和一些关键表现指标约束下，最大化竞得曝光的总价值。例如，在预算和每次点击成本上限的约束下最大化点击量）。这些需求可以是不同的价值类型（如曝光/点击）、约束类型或者约束数量。现有的工作通常关注于一个特定的需求 或者 是几乎没有达到最优解。

在本文中，我们将这些需求建模为约束下竞价问题，并且推导出对于广告主而言，最优出价的一般形式，广告主指通过\(m\)个参数就可以计算最优出价，其中\(m\)是约束数量。在实际应用中，由于拍卖环境的非平稳性，确定参数是不容易的。我们进一步提出了一种强化学习方法来动态调整参数以达到最优，其收敛效率因我们公式中的递归优化特性而得到显著提升。我们将整体的解决方案成为USCB，并在实际工业数据集中实验并证明是有效的，目前已经被部署在阿里巴巴展示广告平台。

问题背景

近些年来，在线展示广告已经是最有影响力的商业形式之一，参与在线竞价的广告主一般会被分成两类，品牌广告和效果广告。品牌广告主寻求长期的增长以及建立用户心智，其广告计划的目标是在约束条件下，将广告展示给尽可能多的受众，约束通常是单次曝光或者点击的平均成本。效果广告主的目标一般是最大化竞得流量的价值，约束一般为单次转化的平均成本。为了满足不同广告主的诉求，广告平台通常会提供多种竞价策略。

之前的工作大多是为了满足广告主的部分需求，关注特定问题形式下的最优出价，本文提出一种通用的解决方案，来满足广告主不同的需求，并且能够部署到真实的广告系统中。

解决方案

假设在一定周期内（比如说一天内），假设存在\(N\)次连续的竞价机会，下标为\(i\)，当广告主的出价\(b_i\)高于其他广告出价中的最高出价\(c_i\)时，广告主可以竞得这个曝光机会，并且成本是\(c_i\)。

广告主的目标是最大化竞得流量的价值\(\max \sum_i v_i x_i\)，其中\(v_i\)是曝光的价值，\(x_i\)是01决策变量，广告主是否要竞得这个曝光。除此之外，广告主通过限定预算和KPI的约束来保证广告投放效率，预算约束\(\sum_i c_i x_i\leq B\)，KPI的约束可以分为两类，一类是成本相关（Cost Related，CR）约束，与广告事件相关，如CPC、CPA等等，另一类是非成本相关约束（Non Cost Related，NCR），如CTR、CPI，KP约束\(j\)的通用形式可以记作 \[ \frac{\sum_i \Bbb{c}_{ij} x_i}{\sum_i \Bbb{p}_{ij} x_i} \leq \Bbb{k}_j \] 其中\(\Bbb{k}_j\)是约束\(j\)的上限，\(\Bbb{p}_{i,j}\)可以是效果的指示变量（是否发生转化）或者常数，\(\Bbb{c}_{ij}=c_i\cdot\Bbb{I}_{\text{CR}_j} + \Bbb{q}_{ij}\cdot(1-\Bbb{I}_{\text{CR}_j})\)，其中\(\Bbb{q}_{ij}\)可以是效果的指示变量或者常数，\(\Bbb{I}_{\text{CR}_j}\)

表示这个约束\(j\)是是否为成本相关约束的指示函数。常见的KPI约束如下表

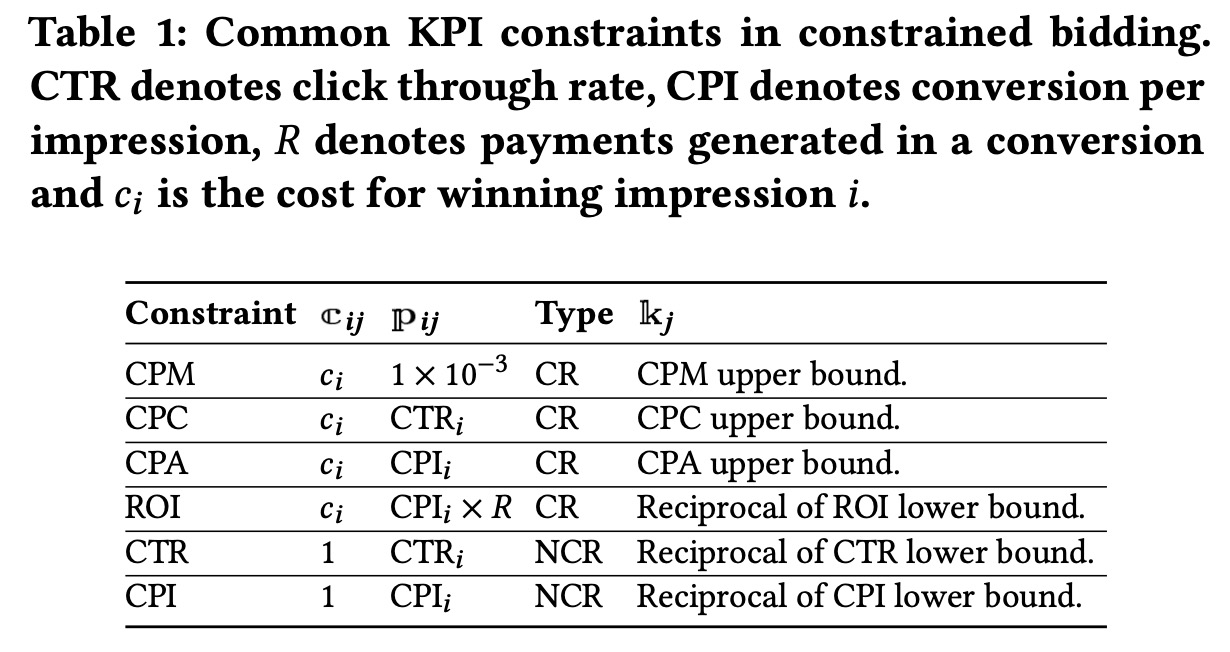
KPI Constraint

整个问题写成线性规划问题(LP1)如下 \[ \begin{aligned} \max && \sum_i v_i x_i \\ \text{s.t.} && \sum_i c_i x_i \leq B \\ && \frac{\sum_i \Bbb{c}_{ij} x_i}{\sum_i \Bbb{p}_{ij} x_i} \leq \Bbb{k}_j && \forall j \\ && x_i \leq 1 && \forall i \\ && x_i \geq 0 && \forall i \\ \end{aligned} \] 该问题的对偶问题(LP2)为 \[ \begin{aligned} \min && B \cdot \alpha + \sum_i r_i \\ \text{s.t.} && c_i\alpha + \sum_j (\Bbb{c}_{ij} - \Bbb{k}_j\Bbb{p}_{ij}) \cdot \beta_j + r_i \geq v_i && \forall i \\ && \alpha, \beta_j, r_i \geq 0 && \forall i \end{aligned} \] 对于其中第一行的约束，我们可以根据\(\Bbb{c}_{ij}\)的定义拆开 \[ \begin{aligned} & c_i\alpha + \sum_j (\Bbb{c}_{ij} - \Bbb{k}_j\Bbb{p}_{ij}) \cdot \beta_j + r_i \geq v_i \\ & c_i\alpha + \sum_j (c_i\cdot\Bbb{I}_{\text{CR}_j} + \Bbb{q}_{ij}\cdot(1-\Bbb{I}_{\text{CR}_j}) - \Bbb{k}_j\Bbb{p}_{ij})\cdot \beta_j + r_i \geq v_i \\ & c_i\alpha + \sum_j c_i \cdot \Bbb{I}_{\text{CR}_j} \cdot \beta_j + \sum_j \big( \Bbb{q}_{ij}\cdot(1-\Bbb{I}_{\text{CR}_j}) - \Bbb{k}_j\Bbb{p}_{ij} \big) \cdot \beta_j +r_i - v_i \geq 0 \\ & c_i \cdot \Big( \alpha + \sum_j \Bbb{I}_{\text{CR}_j} \cdot \beta_j \Big) + \Big( \sum_j \big( \Bbb{q}_{ij}\cdot(1-\Bbb{I}_{\text{CR}_j}) - \Bbb{k}_j\Bbb{p}_{ij} \big) \cdot \beta_j - v_i\Big) + r_i \geq 0 \\ & \underbrace{\Big( v_i - \sum_j \big( \Bbb{q}_{ij}\cdot(1-\Bbb{I}_{\text{CR}_j}) - \Bbb{k}_j\Bbb{p}_{ij} \big) \cdot \beta_j \Big)}_{\text{P}_\text{NCR}} - c_i \cdot \underbrace{\Big( \alpha + \sum_j \Bbb{I}_{\text{CR}_j} \cdot \beta_j \Big)}_{\text{P}_\text{CR}} - r_i \leq 0 \end{aligned} \] 其中\({\text{P}_\text{NCR}}\)表示和成本无关的系数，\({\text{P}_\text{CR}}\)表示和成本相关的系数。根据互补松弛性使得 \[ \begin{aligned} x_i^* \cdot({\text{P}^*_\text{NCR}} - {\text{P}^*_\text{CR}} \cdot c_i -r_i^*) &=0 &\forall i \\ (x^*_i -1) \cdot r_i^* &=0 &\forall i\\ \end{aligned} \] 其中\(*\)表示最优时原问题和对偶问题的解。当出价为\(b^*_i={\text{P}^*_\text{NCR}}/{\text{P}^*_\text{CR}}\)时，满足 \[ \begin{aligned} (b_i^*-c_i)\cdot {\text{P}^*_\text{CR}} - r_i^* &\leq 0 &\forall i\\ x_i^* \cdot\big((b_i^* - c_i)\cdot {\text{P}^*_\text{CR}} -r_i^*\big) &= 0 & \forall i \end{aligned} \] 即广告主最优竞得\(x_i=1\)时，\((b_i^*-c_i)\cdot {\text{P}^*_\text{CR}} - r_i^*=0\)，由于\(r_i^* \geq 0\)且\({\text{P}^*_\text{CR}}\geq0\)，此时\(b_i^*\geq c_i\)，当\(x_i^*=0\)时，此时\(r_i^*=0\)，由于\({\text{P}^*_\text{CR}}\geq0\)，所以\(b_i^*< c_i\)。

综上，当我们采取该出价策略时，可以保证当前竞价策略对于广告主最优。我们将出价的公式写开 \[ \begin{aligned} b_i^* &= \frac{\text{P}^*_\text{NCR}}{\text{P}^*_\text{CR}} \\ &= \frac{ v_i - \sum_j \big( \Bbb{q}_{ij}\cdot(1-\Bbb{I}_{\text{CR}_j}) - \Bbb{k}_j\Bbb{p}_{ij} \big) \cdot \beta_j }{ \alpha + \sum_j \Bbb{I}_{\text{CR}_j} \cdot \beta_j } \\ &=\underbrace{\frac{1}{\alpha + \sum_j \Bbb{I}_{\text{CR}_j} \cdot \beta_j}}_{w_0^*} \cdot v_i - \sum_j \underbrace{\frac{\beta_j}{\alpha + \sum_j \Bbb{I}_{\text{CR}_j} \cdot \beta_j} }_{w_j^*} \cdot \big( \Bbb{q}_{ij}\cdot(1-\Bbb{I}_{\text{CR}_j}) - \Bbb{k}_j\Bbb{p}_{ij} \big) \\ &= w_0^* \cdot v_i +\sum_j w_j^* \cdot \big( \Bbb{q}_{ij}\cdot(1-\Bbb{I}_{\text{CR}_j}) - \Bbb{k}_j\Bbb{p}_{ij} \big) \end{aligned} \] 简化至此，我们发现最优的出价策略其实由M+1个参数控制（M为约束数量）。如果我们可以收集到所有曝光竞价的数据，那么就可以离线求解出最优参数，当曝光竞价数据不完整时，也可以利用后续所有竞价数据调整参数来接近最优出价。

因为不同天流量结构可能存在变化，直到当天结束我们才能获取所有竞价数据，所以我们无法离线求解出最优的竞价参数，但仍可以用历史数据计算初始值。对于实时参数调整，我们采用强化学习的方式进行建模，学习调整参数的策略。相关的定义为：

  • 状态\(\cal{S}\)，广告计划相关特征，包含时间、预算消耗、KPI约束状态等等
  • 动作\(\cal{A}\)，每个时刻\(t\)，每个agent会采取M+1维的动作向量\(\overrightarrow{a_t}=(a_{0t},\cdots,a_{Mt})\)，对应参数向量\(\overrightarrow{w_t}=(w_{0t},\cdots,w_{Mt})\)，下一时刻参数为\(\overrightarrow{w_{t+1}}=\overrightarrow{w_{t}}\cdot(\overrightarrow{a_{t}}+1)\)
  • 奖励\(r_t\)，定义\(r_t\)为当前时刻的目标函数值，\(r_t=\sum_{i\in O_t} v_i\cdot x_i\)，其中\(O_t\)表示\(t\)时刻流量集合
  • 折损系数\(\gamma\)，设置为\(1\)

我们希望学习一个策略\(\pi:\cal{S}\rightarrow \cal{A}\)，最大化累计收益\(R=\sum_{t=1}^T \gamma^{t-1} r_t\)。

竞价请求是按时间先后顺序达到的，但我们需要在全部竞价请求上求得最优解，文中证明了对于求解每个时刻的子问题而言，最优动作序列是将当前参数\(\overrightarrow{w_t}\)修正到\(\overrightarrow{w^*_t}\)并保持。（关于这个证明个人觉得，既正确又废话，当我们对未来流量毫无先验知识的时候，我们只能做同质假设，然后保持现有数据所得到的最优解。）

文中采用DDPG算法来实现该调节，详细如下图，同时由于问题性质以及上述证明的最优的动作序列，有

  • 对于时刻\(t\)，agent会尝试将参数\(\overrightarrow{w_t}\)修正到\(\overrightarrow{w^*_t}\)并保持，而不是逐步调整，这加快了agent的学习速度
  • 评估网络\(Q\)可以简化为\(\cal{G}\)和\(Q(s_t,\overrightarrow{a_t})\)的差异，同时\(\cal{G}\)可以直接看出哪个action可以取得更好的结果，这样会使得整个算法收敛得更快
Algo1

实验分析

在淘宝广告平台，广告主们最常见的出价产品包括：

  • CB{click}，最大化点击，约束是预算，此时最优出价策略是\(b_i=w_0 \cdot \text{pCTR}_i\)
  • CB{click-CPC}，最大化点击，约束是预算和CPC成本，最优出价是\(b_i=w_0\cdot \text{pCTR} +w_1\Bbb{k}_\text{CPC} \cdot \text{pCTR}\)
  • CB{conversion-CPC}，最大化转化，约束是预算和CPC成本，最优出价是\(b_i=w_0\cdot \text{pCVR}_i +w_1\Bbb{k}_\text{CPC} \cdot \text{pCTR}_i\)

这3个数据集都有近4K个广告计划，曝光数约30亿上下，共8天的数据，前7天90%训练，10%验证，最后一天用作测试，采用前7天训练机所有数据来生成测试集的初始参数，我们定义最优参数和初始参数的偏差为 \[ \text{Deviation}=\begin{cases} \sqrt{ \frac{ (w_0/w_0^*-1)^2 + \sum_j (w_j^*-w_j)^2 }{M+1} } && w_0 \leq w_0^* \\ \sqrt{ \frac{ (w_0^*/w_0-1)^2 + \sum_j (w_j^*-w_j)^2 }{M+1} } && w_0 \leq w_0^* \\ \end{cases} \] 不同数据集上初始参数和最优参数的偏差如下图，说明我们的竞价环境非常不稳定，前7天的最优解和当天的最优解差距可能非常大

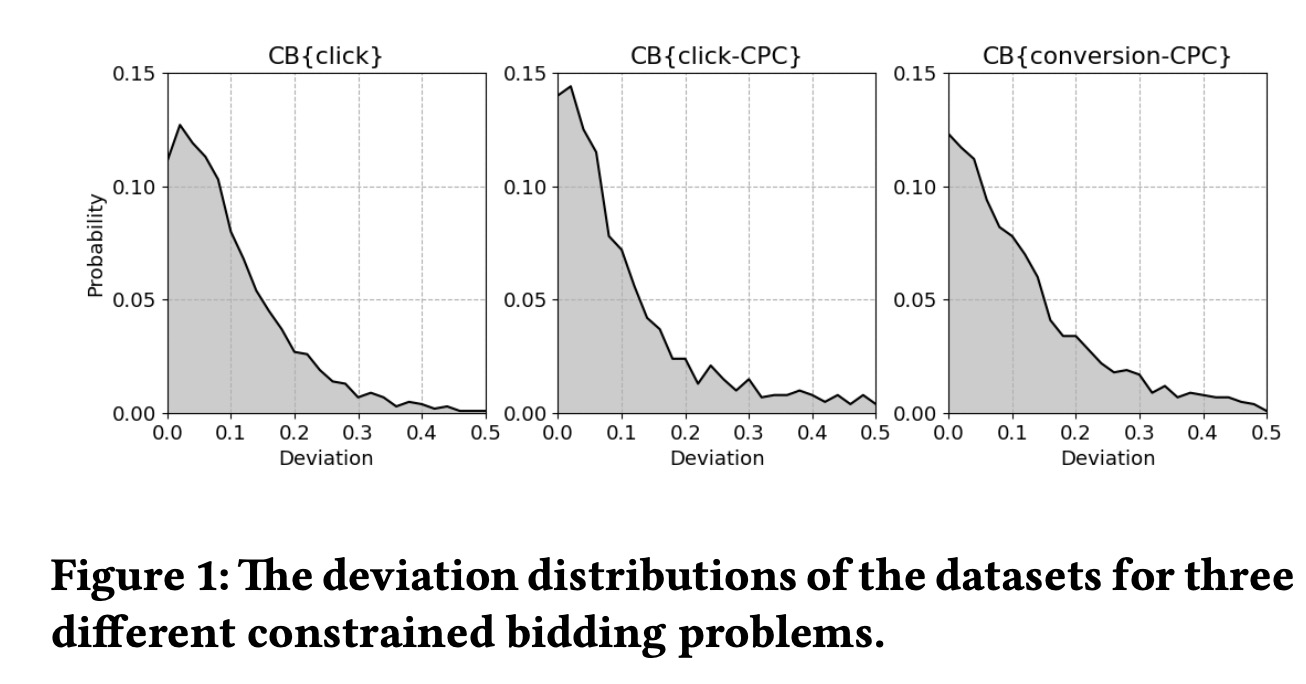
Deviation

实现细节，3层50个节点的全联接来做actor网络和critic网络，batch size 128，回放数据10w，agent调节在\([-0.2,0.2]\)之间连续的参数，每15min调节一次，随机数服从均值0标准差0.05的正态分布，actor网络学习率\(1e^{-6}\)，critic网络学习率\(1e^{-7}\)，违反约束的惩罚为20，最优解用GLPK库离线计算，评估指标为 \[ G=\min\{\frac{R}{R^*},1.0\} - \sum_j p_j \] 其中\(R^*\)为最优解下的最优目标函数值（即最优累计收益），\(p_j=\lambda^{\text{exr}_j}-1\)，表示违反约束情况，违反强度参数\(\text{exr}_j=\max\{0, \Bbb{k}_j^\text{actual}/\Bbb{k}_j -1\}\)。对比模型包括KDD18的DRLB、KDD19的M-PID。（都是一波人的文章，真“我干我自己”）

为了降低环境变动影响，按照不同变动程度做了分层，结果如下

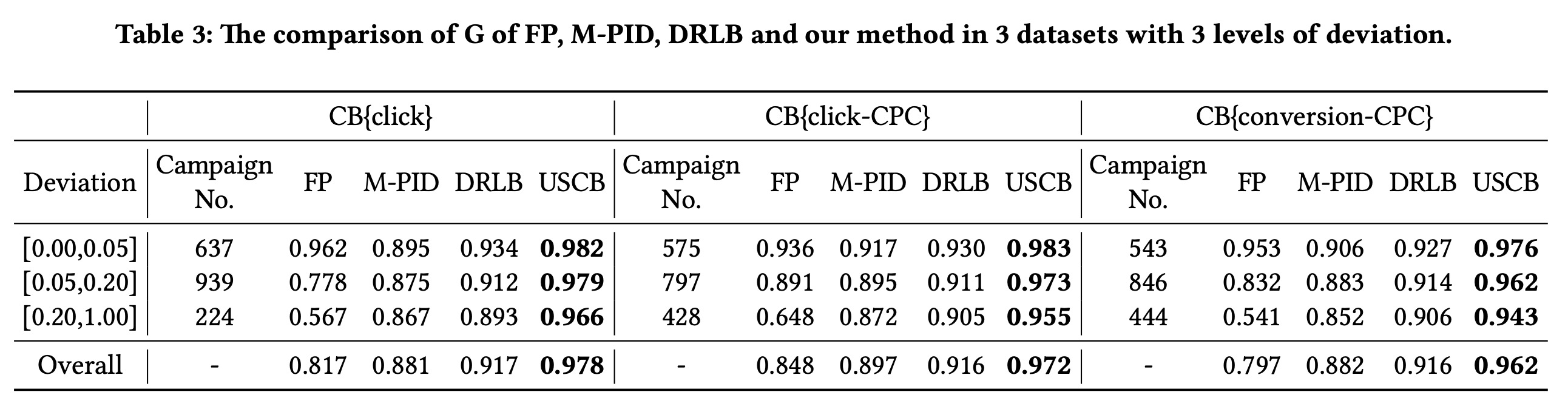
Offline Evaluation

下图展示了某个数据集上适时调整的参数和最优解的比值

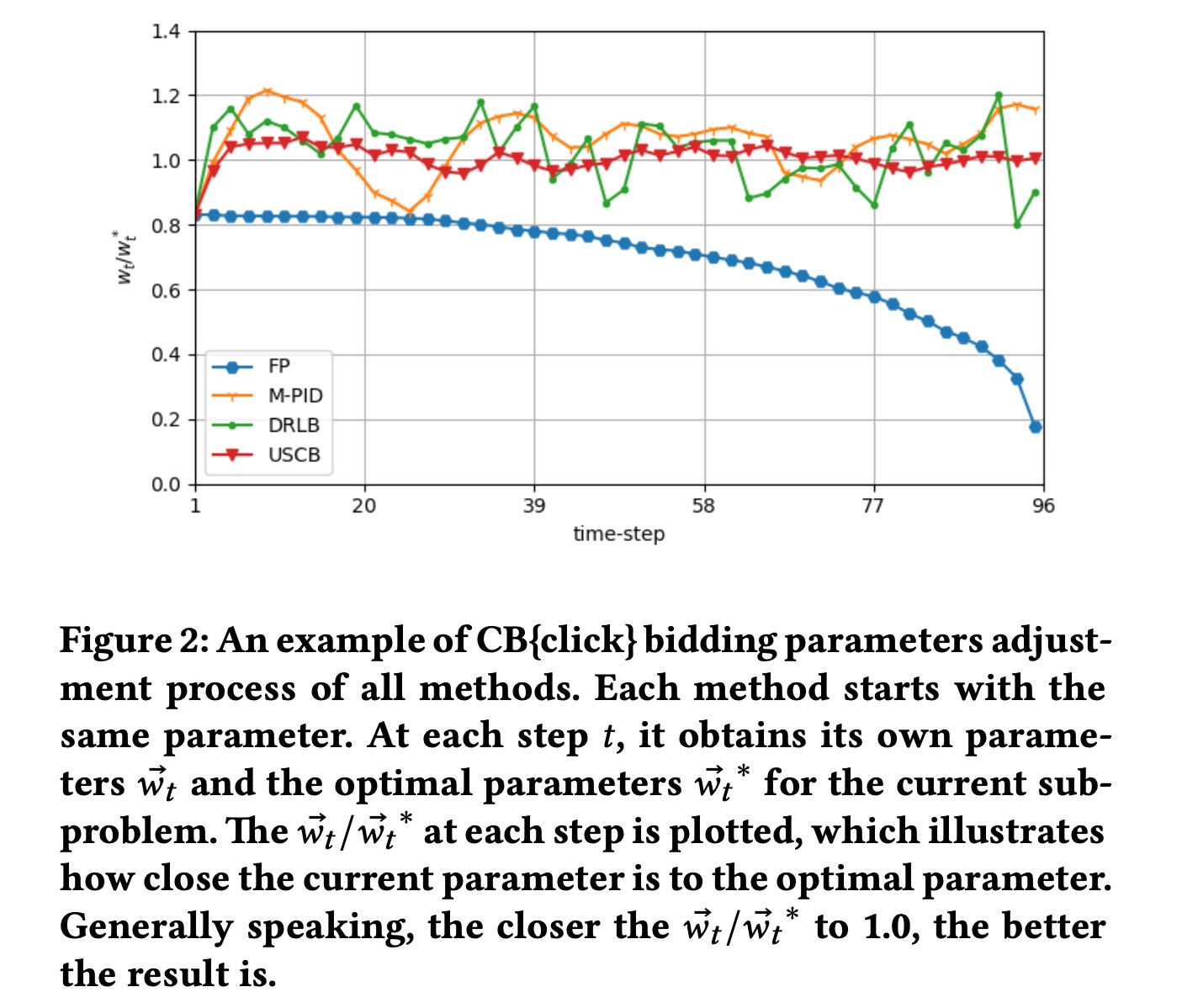
Offline Evaluation 2

M-PID方法主要缺点在于需要先验知识设定目标，同时需要调节超参数。USCB相比DRLB主要是收敛效率所带来的稳定性优势。

关于收敛效率，文中认为是由于问题形式导致critic网络的效果非常好，进而提升了actor网络学习策略的效率。

违反约束罚项，更多是超参数的调整。

总结

所提出的框架对于端内广告的出价而言，的确是非常有效且适用面很广，目前该算法在某场景21年初就已全量。

个人觉得，从KDD19那篇文章开始，端内广告出价问题基本上已经算是被研究透了，本文更多是做一些修补和扩展的工作。